Using Excel Tools to Handle Nested and Random Factors in ANOVA
Some experiments rely on settings that are to some degree intact and therefore not subject to experimental manipulation. For example, some medical research takes place in hospitals. It's often true that the experimenter cannot manipulate certain aspects of how the hospital manages health care.
Nested Factors
Suppose that an experimenter wants to investigate the effect of cardiologists' use of digital handheld devices on the success that patients have in managing their blood pressure. If doctors use digital devices to immediately access full in-patient records, modify prescriptions, and arrange changes in diets, hypertensive patients might be able to keep their blood pressure under control more effectively than in hospitals where more traditional procedures are followed.
The difficulty that might confront the experimenter is that hospitals either offer doctors that sort of digital tool or they don't. Only hospitals in transition would have some cardiologists using digital technology; and others relying on paper charts, manual prescriptions, and dietary orders.
So the experimental design might call for a factor called Digital Device Usage, which records whether a participating hospital uses the sort of digital technology that's under evaluation. The experimenter might work with two hospitals that use the technology and two that don't. At each hospital, there might be a random sample of 4 in-patients who have been in treatment for between 7 and 10 days.
What does this design look like? One way to depict it is shown in Figure 1.
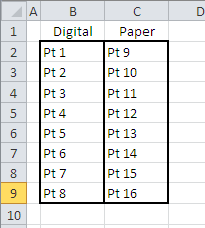
Figure 1 This layout ignores Hospital as a factor in the experiment
In a sense, Figure 1 represents the experimental design. There are 16 patients, 8 in each "treatment" category: The doctor either uses digital technology or traditional pencil-and-paper methods.
But the layout in Figure 1 fails to account for any Hospital effect. As described above, there are four hospitals involved. Figure 2 shows a layout that provides hospital information.
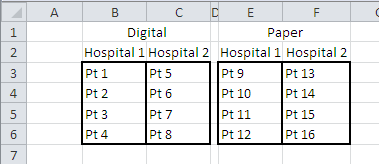
Figure 2 This layout includes Hospital as a factor in the experiment, but it does so inaccurately
The design shown in Figure 2 is called a crossed factorial design. The term factorial simply means that there are two (or more) factors involved: Treatment and Hospital. The term crossed means that each level of each factor appears at each level of the other factor. So, for example, Hospital 1 has patients whose doctors use digital equipment and it also has patients whose doctors use traditional storage-and-retrieval methods. Treatment crosses Hospital.
But this is not how the actual design was described. There are four hospitals, not two, and each hospital employs only one level of the treatment: either digital or traditional, and not both. Figure 3 shows an accurate layout of this design.
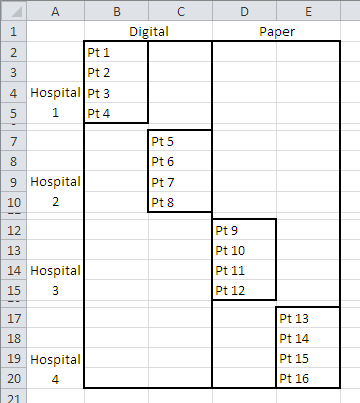
Figure 3 This layout shows how the Hospital factor is nested within the Treatment factor
The design as described, and as laid out in Figure 3, is termed a nested factorial design. Each level of one factor appears with only one level of the other factor. Here, Hospitals 1 and 2 appear only with the Digital treatment, and Hospitals 3 and 4 appear only with the Traditional treatment.
So why should we care about a Hospital factor at all? The reason is that there may well be something about the medical care at a given hospital (or hospitals) that affects heart patients' response, quite independent of and apart from the technology, digital versus traditional, used by the medical staff.
If we ignore the Hospital factor entirely, as suggested in Figure 1, we miss any effect it may have, either attributing it to the Treatment factor or losing it in the error variance.
We might act as if the layout in Figure 2 represents reality, combining Hospitals 1 and 2, and Hospitals 3 and 4. But that gets us right back to the layout shown in Figure 1.
Therefore, we apply the nested design shown in Figure 3, including some modifications to the statistical analysis.
Nuisance Factors
In the example that this paper has been considering, you can consider Hospital as a "nuisance" factor. The experimenter is not interested in differences in patient outcomes across hospitals. The interest centers on differences in patient outcomes that can be attributed to the use of newer information technologies.
But the nature of the treatment delivery system forces the experimenter to pay attention to Hospital as a factor. At the time when the experiment takes place, only a small subset of hospitals use both traditional and newer technologies, and they do so only because they are in transition.
The experiment, therefore, can't ignore a possible Hospital factor because it might exert an influence on the outcomes achieved by cardiac patients—despite the fact that a Hospital effect isn't of interest to the experimenter. That's why such factors are sometimes termed nuisance factors: You're not really interested in them, but you have to take account of them.
Not all nested factors are nuisance factors, by any means. But it is true that nuisance factors tend to be nested, due to the realities of many experimental test beds.
Random Factors and Fixed Factors
It's also true that the experimenter in this example wants to investigate the differential effects of using handheld digital devices on the effectiveness of cardiac care, versus traditional methods of storing and retrieving patient information. The experimenter isn't interested in any other information management methods. The experiment isn't intended to generalize its findings to other methods: Its purpose is restricted to comparing outcomes that are associated with two specific methods. The Treatment factor in this example is therefore referred to as a fixed factor. The experimenter's interest is fixed on the treatments that are employed in the experiment.
In contrast, the experimenter does not want to restrict the findings to the four particular hospitals in which the research takes place. The four hospitals are randomly selected, from the population of hospitals in which doctors use handheld devices and from the population of hospitals in which the doctors don't. The Hospital factor is therefore termed a random factor.
Designs in which there is just one factor, and that factor is fixed, are among the most frequently used in the literature, whether that literature consists of market research, operations research, medical research or behavioral research. Factorial designs that employ two or more fixed factors, usually fully crossed with one another, are also popular approaches because they often bring about greater statistical power than do single factor experiments, and because they often use scarce resources more efficiently.
Another useful design is called a mixed model. A mixed model uses one or more fixed factors and one or more random factors. The example discussed earlier in this paper is a mixed model: It uses a fixed Treatment factor and a random Hospital factor.
Both mixed models and nested models call for different analysis of variance (ANOVA) computations than does a design with two fixed and crossed factors. Major differences exist in the formulas. If you use calculations that are intended for a crossed design and fixed factors when you should be using the calculations for a nested or mixed design, you can easily mistake an effect that is highly significant for one that few would consider significant.
If you have an equal number of observations in each design cell, however, the ANOVA: Two-Factor With Replication tool (part of Excel's Data Analysis add-in) is easily capable of handling both mixed models and models with a nested factor. A small amount of tweaking, after the fact, is needed.
I describe that additional work in the second paper of this series, Using Excel with Mixed and Nested Models.