Forcing the Constant in Regression to Zero: Understanding Excel's LINEST() Error

Like this article? We recommend

Predictive Analytics: Microsoft Excel

Learn More Buy

Like this article? We recommend

Like this article? We recommend 

Predictive Analytics: Microsoft Excel

Learn More Buy

One of the options that has always been available in Excel's LINEST() worksheet function is the const argument, short for constant. The function's syntax is:

=LINEST(Y values, X values, const, stats)

where:

• Y values represents the range that contains the outcome variable (or the variable that is to be predicted by the regression equation).
• X values represents the range that contains the variable or variables that are used as predictors.
• const is either TRUE or FALSE, and indicates whether LINEST() should include a constant (also called an intercept) in the equation, or should omit the constant. If const is TRUE or omitted, the constant is calculated and included. If const is FALSE, the constant is omitted from the equation.
• stats, if TRUE, tells LINEST() to include statistics that are helpful in evaluating the quality of the regression equation as a means of gauging the strength of the relationship between the Y values and the X values.

Setting the const argument to FALSE can easily have major implications for the nature of the results that LINEST() returns. And there is a real question of whether the const argument is a useful option at all. In fact, the question is not limited to LINEST() and Excel. It extends to the whole area of regression analysis, regardless of the platform used to carry out the regression.

Some credible practitioners believe that it's important to force the constant to zero in certain situations, usually in the context of regression discontinuity designs.

Others, including myself, believe that if setting the constant to zero appears to be a useful and informative option, then linear regression itself is often the wrong model for the data.

The Excel 2003 Through 2010 Versions

Figure 1 shows an example of the difference between LINEST() results when the constant is calculated normally, and when it is forced to equal zero.

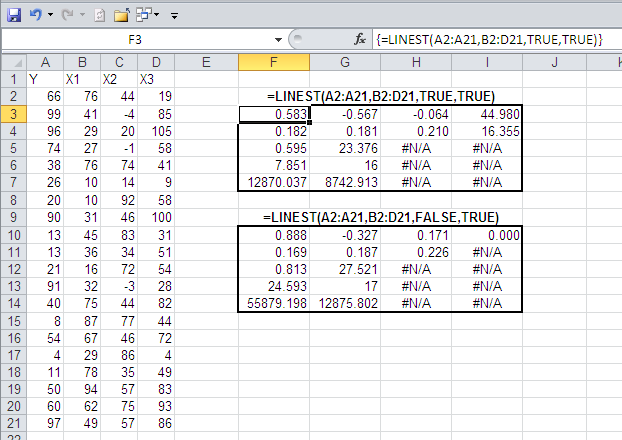
Figure 1 LINEST() returns the same results, whether you use Excel 2003 or Excel 2010.

In Figure 1, the two sets of results are based on the same underlying data set, with the Y values in A2:A21 and the X values in B2:D21. The first set of results in F3:I7 is based on a constant calculated normally (const = TRUE). The second set of results in F10:I14 is based on a constant that is forced to equal zero (const = FALSE).

Notice that not a single value in the results is the same when the constant is forced to zero as when the constant is calculated normally.

Basing the Deviations on the Means

Figure 2 begins to demonstrate how this comes about.

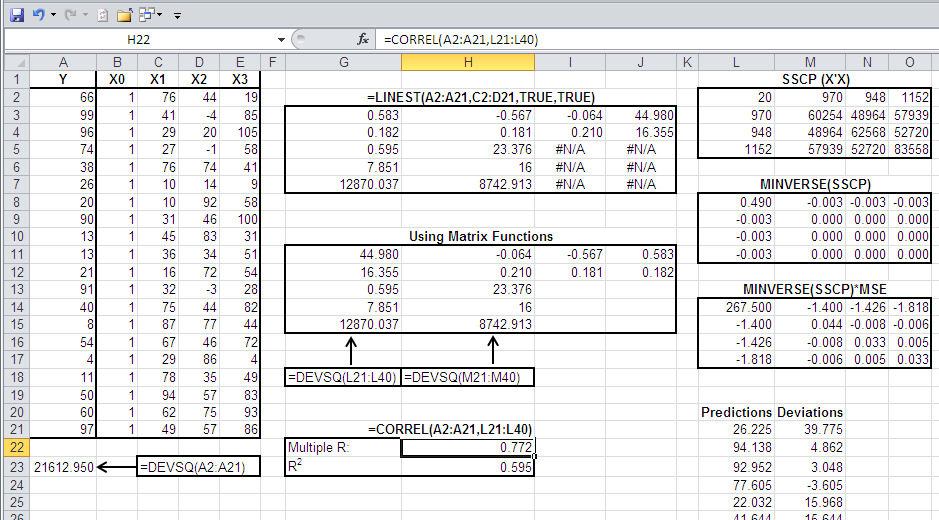
Figure 2 The deviations are centered on the means.

In Figure 2, cells G15:H15 contain the sums of squares for the regression and the residual, respectively. They are based on the predicted Y values, in L21:L40, and the deviations of the predicted values from the actuals, in M21:LM40.

The sums of squares are calculated by means of the DEVSQ() function, which subtracts every value in the argument's range from the mean of those values, squares the result, and sums the squares.

The value in cell G13, 0.595, is the R² for the regression. One useful way to calculate that figure (and a useful way to think of it) is:

=G15/(G15+H15)

That is, R² is the ratio of the sum of squares regression to the total sum of squares of the Y values. The result, 0.595, states that 59.5% of the variability in the Y values is attributable to variability in the composite of the X values.

Notice in Figure 2 that the statistics reported in G11:J15 are identical to those reported in G3:J7 (except that LINEST() reports the regression coefficients and their standard errors in the reverse of worksheet order). The former are calculated using Excel's matrix functions; the latter are calculated using the LINEST function.

Also notice in Figure 2 that the correlation between the actual and the predicted Y values is given in cell H22. It is 0.772. The square of that correlation, in cell H23, is 0.595—that is of course R², the same value that you get by calculating the ratio of the sum of squares regression to the total sum of squares.

There's nothing magical about any of this. It's all as is expected according to the mathematics underlying regression analysis.

Changing the Deviation Basis to Zero

Now examine the same sort of analysis shown in Figure 3.

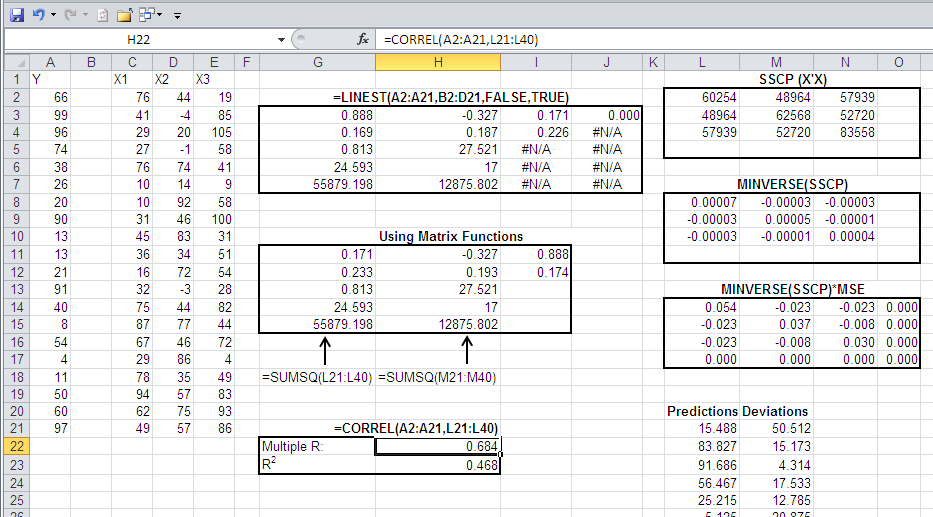
Figure 3 The deviations are centered on zero.

Notice the values for the sum of squares regression and the sum of squares residual in Figure 3. They are both much larger than the sums of squares reported in Figure 2. The reason is that the deviations that are squared and summed in Figure 3 are the differences between the values and zero, not between the values and their mean.

This change in the nature of the deviations always increases the total sum of squares. (For the reason that this is so, see Statistical Analysis: Microsoft Excel 2010, Que, 2011, Chapter 2.)

The change from centering the predicted values on their mean, and the errors in prediction on their mean, also changes the relative size of the sums of squares. It can happen that the sum of squares regression gets larger relative to the sum of squares residual, and the result is to increase the apparent value of R². Using the sums of squares shown in Figure 2 and Figure 3, for example:

Figure 2:

12870.037 / (12870.037 + 8742.913) = .595 

(Compare with cells G5 and G13.)

Figure 3:

55879.198 / (55879.198 + 12875.802) = .813

(Compare with cells G5 and G13.)

So the suppression of the constant in Figure 3 has resulted in an increase in the R² from .595 to .813, and that's a substantial increase. But does it really mean that the regression equation that's returned in Figure 3 is more accurate than the one returned in Figure 2? After all, the square root of R² is the multiple correlation between the actual Y values and the composite, predicted Y values. The higher that correlation, the more accurate the prediction.

How the Deviations Affect the R²

We can test that accuracy by calculating the correlations, squaring them, and comparing the results to the values for R² that are returned under the two conditions for the constant: present and absent.

Look first again at Figure 2. There, the multiple R is calculated at .772, and the multiple R² is calculated at .595 (cells H22 and H23). The value of .595 agrees with the value returned by LINEST() in cell G5, and by the ratio of the sums of squares in cell G13.

Now return to Figure 3. There, the multiple R is calculated at .684, and the multiple R² is calculated at .468 (cells H22 and H23). But the value of .468 does not agree with the value returned by LINEST() in cell G5, and by the ratio of the sums of squares in cell G13.

In sum, running LINEST() on the data shown in Figure 2 and Figure 3 has these effects on the apparent accuracy of the predictions:

• The R² reported by LINEST() without the constant is higher than that reported by LINEST() with the constant.
• The accuracy of the regression equation when evaluated by means of the correlation between the actual Y values and the predicted Y values is lower when the regression equation omits the constant.

This is an inconsistency, even an apparent contradiction. Regarded as a ratio of sums of squares, R² is higher without the constant. Regarded as the square of the correlation between the actual and predicted Y values, R² is lower without the constant.

The Constant and the Deviations

Of course, the problem is due to the fact that in omitting the constant, we are redefining what's meant by the term "sum of squares." As a result, we're dismembering the meaning of the R².

When you include the constant, the deviations are the differences between the observed values and their mean—that's what "least squares" is all about. When you omit the constant, the deviations are the differences between the observed values and zero—that's what "regression without the constant" is all about.

If the predicted values happen to be generally farther from zero than from their own mean, then the sum of squares regression will be inflated as compared to regression with the constant. In that case, the R² will tend to be greater without the constant in the regression equation than it is with the constant.

A Negative R²?

Finally, suppose you're still using a version of Excel through Excel 2002, and you have used LINEST(), without the constant, on a data set such as the one shown in Figure 4.

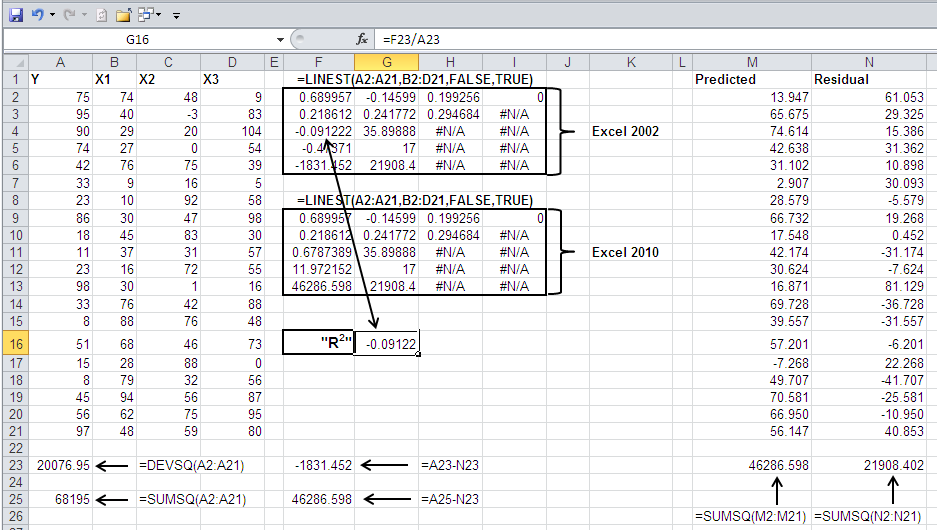
Figure 4 A negative R² is possible only if someone has made a mistake.

Even the idea of a negative R² is ridiculous. Outside the realm of imaginary numbers, the square of a number cannot be negative, and ordinary least squares analysis does not involve imaginary numbers. How does the R² value of -0.09122 in cell F4 of Figure 4 get there?

For that matter, how does Excel 2002 come up with a negative sum of squares regression and a negative F ratio (cells F6 and F5 respectively in Figure 4)? If the square of a number must be positive, then the sum of squared numbers must also be positive. And an F ratio is the ratio of two variances. A variance is an average of squared deviations, and therefore must also be positive—and the ratio of two positive numbers must also be positive.

How to Get a Negative R²

The answer is poorly informed coding. Recall that, when the constant is calculated normally, the total sum of squares of the actual Y values equals the total of the sum of squares regression and the sum of squares residual. For example, in Figure 2, the total sum of squares is shown in cell A23 at 21612.950. It is returned by Excel's DEVSQ() function, which sums the squared deviations of each value from the mean of the values.

Also in Figure 2, the sum of squares regression and the sum of squares residual are shown in cells G15:H15. The total of those two figures is 21612.950: the value of the total sum of squares in cell A23.

Therefore, one way to calculate the sum of squares regression is to subtract the sum of squares residual from the total sum of squares. Another method, of course, is to calculate the sum of squares regression directly on the predicted values. But if you're writing the underlying code in, say, C, it's much quicker to get the sum of squares regression by subtraction than by doing the math from scratch on the predicted values.

When the constant is forced to zero, the sum of squares residual that's returned in all versions of Excel equals the result of pointing SUMSQ(), not DEVSQ(), at the residual values. This is entirely correct, given that you want to force the constant to zero.

The sum of squares residual using the normal calculation of the constant is as follows:

Residual = Actual – Predicted

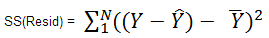
That is, find each of N residual values, which is the actual Y value less the predicted Y value (Ŷ). Subtract the mean of the residuals (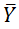) from each residual, square the difference, and sum the squared differences. Excel's DEVSQ() function does precisely this.

The sum of squares residual forcing the constant to zero is as follows:

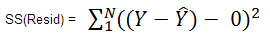
or, more simply:

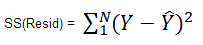
Excel's SUMSQ() function does precisely this.

The Mistake, Corrected—In Part

Now, what LINEST() did in Excel version 2002 (and earlier) was to use the equivalent of SUMSQ() to get the sum of squares residual, but the equivalent of DEVSQ() to get the total sum of squares. If you add SUMSQ(Predicted values) to SUMSQ(Residual values), you get SUMSQ(Actual values).

But only in the situation where the mean of the actual values is zero can SUMSQ(Predicted values) plus SUMSQ(Residual values) equal DEVSQ(Actual values).

The problem has been corrected in Excel 2003 and subsequent versions. But as late as Excel 2010, the problem lives on in Excel charts. If you add a linear trendline to a chart, call for it to force the constant to zero, and display the R² value on the chart, it can still show up as a negative number. See Figure 5.

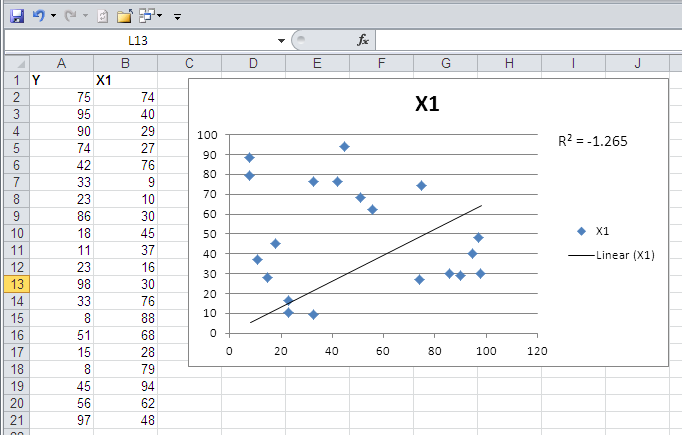
Figure 5 A negative R² can still appear with a chart's trendline.

Notice in Figure 5 that although Excel 2010 was used to produce the chart, the linear trendline's properties include a negative R² value. (The equation would be correct, though, if you chose to show it along with R².)

Conclusion

This series of papers on how Microsoft has implemented LINEST() concludes with a discussion of Microsoft's extraordinary decision regarding how to handle extreme multicollinearity in the X variables.