- 1.1 Introduction
- 1.2 Scope of Treatment
- 1.3 Analysis and Design
- 1.4 Conditions of Equilibrium
- 1.5 Definition and Components of Stress
- 1.6 Internal Force-Resultant and Stress Relations
- 1.7 Stresses on Inclined Sections
- 1.8 Variation of Stress Within a Body
- 1.9 Plane-Stress Transformation
- 1.10 Principal Stresses and Maximum in-plane Shear Stress
- 1.11 Mohr's Circle for Two-Dimensional Stress
- 1.12 Three-Dimensional Stress Transformation
- 1.13 Principal Stresses in Three Dimensions
- 1.14 Normal and Shear Stresses on an Oblique Plane
- 1.15 Mohr's Circles in Three Dimensions
- 1.16 Boundary Conditions in Terms of Surface Forces
- 1.17 Indicial Notation
- References
- Problems
1.3 Analysis and Design
Throughout this text, a fundamental procedure for analysis in solving mechanics of solids problems is used repeatedly. The complete analysis of load-carrying structural members by the method of equilibrium requires consideration of three conditions relating to certain laws of forces, laws of material deformation, and geometric compatibility. These essential relationships, called the basic principles of analysis, are:
- Equilibrium Conditions. The equations of equilibrium of forces must be satisfied throughout the member.
- Material Behavior. The stress–strain or force-deformation relations (for example, Hooke's law) must apply to the material behavior of which the member is constructed.
- Geometry of Deformation. The compatibility conditions of deformations must be satisfied: that is, each deformed portion of the member must fit together with adjacent portions. (Matter of compatibility is not always broached in mechanics of materials analysis.)
The stress and deformation obtained through the use of the three principles must conform to the conditions of loading imposed at the boundaries of a member. This is known as satisfying the boundary conditions. Applications of the preceding procedure are illustrated in the problems presented as the subject unfolds. Note, however, that it is not always necessary to execute an analysis in the exact order of steps listed previously.
As an alternative to the equilibrium methods, the analysis of stress and deformation can be accomplished by employing energy methods (Chap. 10), which are based on the concept of strain energy. The aspect of both the equilibrium and the energy approaches is twofold. These methods can provide solutions of acceptable accuracy where configurations of loading and member shape are regular, and they can be used as the basis of numerical methods (Chap. 7) in the solution of more realistic problems.
Engineering design is the process of applying science and engineering techniques to define a structure or system in detail to allow its realization. The objective of a mechanical design procedure includes finding of proper materials, dimensions, and shapes of the members of a structure or machine so that they will support prescribed loads and perform without failure. Machine design is creating new or improved machines to accomplish specific purposes. Usually, structural design deals with any engineering discipline that requires a structural member or system.
Design is the essence, art, and intent of engineering. A good design satisfies performance, cost, and safety requirements. An optimum design is the best solution to a design problem within given restrictions. Efficiency of the optimization may be gaged by such criteria as minimum weight or volume, optimum cost, and/or any other standard deemed appropriate. For a design problem with many choices, a designer may often make decisions on the basis of experience, to reduce the problem to a single variable. A solution to determine the optimum result becomes straightforward in such a situation.
A plan for satisfying a need usually includes preparation of individual preliminary design. Each preliminary design involves a thorough consideration of the loads and actions that the structure or machine has to support. For each situation, an analysis is necessary. Design decisions, or choosing reasonable values of the safety factors and material properties, are significant in the preliminary design process.
The role of analysis in design may be observed best in examining the phases of a design process. This text provides an elementary treatment of the concept of "design to meet strength requirements" as those requirements relate to individual machine or structural components. That is, the geometrical configuration and material of a component are preselected and the applied loads are specified. Then, the basic formulas for stress are employed to select members of adequate size in each case. The following is rational procedure in the design of a load-carrying member:
- Evaluate the most likely modes of failure of the member. Failure criteria that predict the various modes of failure under anticipated conditions of service are discussed in Chapter 4.
- Determine the expressions relating applied loading to such effects as stress, strain, and deformation. Often, the member under consideration and conditions of loading are so significant or so amenable to solution as to have been the subject of prior analysis. For these situations, textbooks, handbooks, journal articles, and technical papers are good sources of information. Where the situation is unique, a mathematical derivation specific to the case at hand is required.
- Determine the maximum usable value of stress, strain, or energy. This value is obtained either by reference to compilations of material properties or by experimental means such as simple tension test and is used in connection with the relationship derived in step 2.
-
Select a design factor of safety. This is to account for uncertainties in a number of aspects of the design, including those related to the actual service loads, material properties, or environmental factors. An important area of uncertainty is connected with the assumptions made in the analysis of stress and deformation. Also, we are not likely to have a secure knowledge of the stresses that may be introduced during machining, assembly, and shipment of the element.
The design factor of safety also reflects the consequences of failure; for example, the possibility that failure will result in loss of human life or injury or in costly repairs or danger to other components of the overall system. For these reasons, the design factor of safety is also sometimes called the factor of ignorance. The uncertainties encountered during the design phase may be of such magnitude as to lead to a design carrying extreme weight, volume, or cost penalties. It may then be advantageous to perform thorough tests or more exacting analysis rather to rely on overly large design factors of safety.
The true factor of safety, usually referred to simply as the factor of safety, can be determined only after the member is constructed and tested. This factor is the ratio of the maximum load the member can sustain under severe testing without failure to the maximum load actually carried under normal service conditions, the working load. When a linear relationship exists between the load and the stress produced by the load, the factor of safety n may be expressed as
Equation 1.1
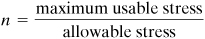
Maximum usable stress represents either the yield stress or the ultimate stress. The allowable stress is the working stress. The factor of safety must be greater than 1.0 if failure is to be avoided. Values for factor of safety, selected by the designer on the basis of experience and judgment, are about 1.5 or greater. For most applications, appropriate factors of safety are found in various construction and manufacturing codes.
The foregoing procedure is not always conducted in as formal a fashion as may be implied. In some design procedures, one or more steps may be regarded as unnecessary or obvious on the basis of previous experience. Suffice it to say that complete design solutions are not unique, involve a consideration of many factors, and often require a trial-and-error process [Ref. 1.6]. Stress is only one consideration in design. Other phases of the design of components are the prediction of the deformation of a given component under given loading and the consideration of buckling (Chap. 11). The methods of determining deformation are discussed in later chapters. Note that there is a very close relationship between analysis and design, and the examples and problems that appear throughout this book illustrate that connection.
We conclude this section with an appeal for the reader to exercise a degree of skepticism with regard to the application of formulas for which there is uncertainty as to the limitations of use or the areas of applicability. The relatively simple form of many formulas usually results from rather severe restrictions in its derivation. These relate to simplified boundary conditions and shapes, limitations on stress and strain, and the neglect of certain complicating factors. Designers and stress analysts must be aware of such restrictions lest their work be of no value or, worse, lead to dangerous inadequacies.
In this chapter, we are concerned with the state of stress at a point and the variation of stress throughout an elastic body. The latter is dealt with in Sections 1.8 and 1.16 and the former in the balance of the chapter.