- 1.1 Introduction
- 1.2 Scope of Treatment
- 1.3 Analysis and Design
- 1.4 Conditions of Equilibrium
- 1.5 Definition and Components of Stress
- 1.6 Internal Force-Resultant and Stress Relations
- 1.7 Stresses on Inclined Sections
- 1.8 Variation of Stress Within a Body
- 1.9 Plane-Stress Transformation
- 1.10 Principal Stresses and Maximum in-plane Shear Stress
- 1.11 Mohr's Circle for Two-Dimensional Stress
- 1.12 Three-Dimensional Stress Transformation
- 1.13 Principal Stresses in Three Dimensions
- 1.14 Normal and Shear Stresses on an Oblique Plane
- 1.15 Mohr's Circles in Three Dimensions
- 1.16 Boundary Conditions in Terms of Surface Forces
- 1.17 Indicial Notation
- References
- Problems
1.15 Mohr's Circles in Three Dimensions
Consider a wedge shown in Fig. 1.25a, cut from the cubic element subjected to triaxial stresses (Fig. 1.22a). The only stresses on the inclined x' face (parallel to the z axis) are the normal stress s x' and the shear stress t x'y' acting in the x'y' plane. Inasmuch as the foregoing stresses are determined from force equilibrium equations in the x'y' plane, they are independent of the stress s 3. Thus, the transformation equations of plane stress (Sec. 1.9) and Mohr's circle can be employed to obtain the stresses s x' and t x'y' . The foregoing conclusion is also valid for normal and shear stresses acting on inclined faces cut through the element parallel to the x and y axes.
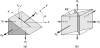
Figure 1.25 Triaxial state of stress: (a) wedge; (b) planes of maximum shear stress.
The stresses acting on elements oriented at various angles to the principal axes can be visualized with the aid of Mohr's circle. The cubic element (Fig. 1.22a) viewed from three different directions is sketched in Figs. 1.26a to c. A Mohr's circle is drawn corresponding to each projection of an element. The cluster of three circles represents Mohr's circles for triaxial stress (Fig. 1.26d). The radii of the circles are equal to the maximum shear stresses, as indicated in the figure. The normal stresses acting on the planes of maximum shear stresses have the magnitudes given by the abscissa as of the centers of the circles.
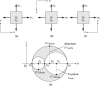
Figure 1.26 (a–c) Views of elements in triaxial stresses on different principal axes; (d) Mohr's circles for three-dimensional stress.
The largest shear stresses occur on planes oriented at 45° to the principal planes. The shear stress is a maximum located as the highest point on the outer circle. The value of the absolute maximum shearing stress is therefore
Equation 1.45
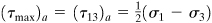
acting on the planes that bisect the planes of the maximum and minimum principal stresses, as shown in Fig. 1.25b. It is noted that the planes of maximum shear stress may also be ascertained by substituting n 2 = 1 – l 2 – m 2 into Eq. (1.38b), differentiating with respect to l and m, and equating the resulting expressions to zero (Prob. 1.80).
Determining the absolute value of maximum shear stress is significant when designing members made of ductile materials, since the strength of the material depends on its ability to resist shear stress (Sec. 4.6). Obviously, as far as the stress magnitudes are concerned, the largest circle is the most significant one. However, all stresses in their various transformations may play a role in causing failure, and it is usually instructive to plot all three principal circles of stress, as depicted in the figure. An example of this type occurs in thin-walled pressurized cylinders, where s q = s 1, s a = s 2, and s r = s 3 = 0 at the outer surface (Table 1.1). It is also interesting to note that, in special cases, where two or all principal stresses are equal, a Mohr's circle becomes a point.
Equations of Three Mohr's Circles for Stress
It has been demonstrated that, given the values of the principal stresses and of the direction cosines for any oblique plane (Fig. 1.22b), the normal and shear stresses on the plane may be ascertained through the application of Eqs. (1.37) and (1.38). This may also be accomplished by means of a graphical technique due to Mohr [Refs. 1.10 through 1.12]. The latter procedure was used in the early history of stress analysis, but today it is employed only as a heuristic device.
In the following discussion, we demonstrate that the aforementioned equations together with the relation l 2 + m 2 + n 2 = 1 are represented by three circles of stress, and the coordinates (s, t) locate a point in the shaded area of Fig. 1.26d [Ref. 1.13]. These simultaneous equations are
Equation a
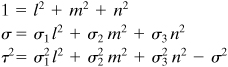
where l
2 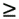 0, m
2
0, m
2 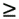 0, and n
2
0, and n
2 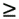 0. Solving for the direction cosines, results in
0. Solving for the direction cosines, results in
Equation 1.46
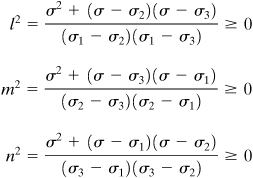
Inasmuch as s 1 > s 2 > s 3, the numerators of Eqs. (1.46) satisfy
Equation b
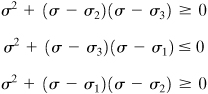
as the denominators of Eqs. (1.46) are (s 1 – s 2) > 0 and (s 1 – s 3) > 0, (s 2 – s 3) > 0 and (s 2 – s 1) < 0, (s 3 – s 1) < 0 and (s 3 – s 2) < 0, respectively.
Finally, the preceding inequalities may be expressed as follows
Equation 1.47
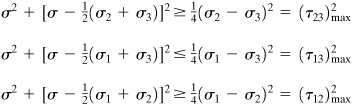
Equations (1.47) represent the formulas of the three Mohr's circles for stress, shown in Fig. 1.26d. Stress points (s, t) satisfying the equations for circles centered at C 1 and C 2 lie on or outside circles, but for the circle centered at C 3 lie on or inside circle. We conclude therefore that an admissible state of stress must lie on Mohr's circles or within the shaded area enclosed by these circles.
Example 1.8. Analysis of Three-Dimensional Stresses in a Member
The state of stress on an element of a structure is illustrated in Fig. 1.27a. Using Mohr's circle, determine (a) the principal stresses and (b) the maximum shearing stresses. Show results on a properly oriented element. Also, (c) apply the equations developed in Section 1.14 to calculate the octahedral stresses.
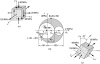
Figure 1.27 Example 1.8. (a) Element in three-dimensional stress; (b) Mohr's circles of stress; (c) stress element for 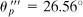 .
.
Solution
- First, Mohr's circle for the transformation of stress in the xy plane is sketched in the usual manner as shown, centered at C
2 with diameter A
2
A
3 (Fig. 1.27b). Next, we complete the three-dimensional Mohr's circle by drawing two additional circles of diameters A
1
A
2 and A
1
A
3 in the figure. Referring to the circle, the principal stresses are s
1 = 100 MPa, s
2 = 40 MPa, and s
3 = –60 MPa. Angle
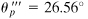 , as tan
, as tan 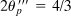 . The results are sketched on a properly oriented element in Fig. 1.27c.
. The results are sketched on a properly oriented element in Fig. 1.27c. -
The absolute maximum shearing stress, point B 3, equals the radius of the circle centered at C 3 of diameter A 1 A 3. Thus,
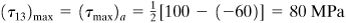
The maximum shearing stress occurs on the planes 45° from the y' and z faces of the element of Fig. 1.27c.
-
The octahedral normal stress, from Eq. (1.44), is
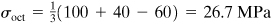
The octahedral shearing stress, using Eq. (1.43), is
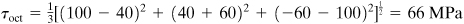
Comments A comparison of the results (see Fig. 1.27b) shows that
|
s oct < s 1 |
and |
t oct < (t max) a |
That is, the maximum principal stress and absolute maximum shear stress are greater than their octahedral counterparts.