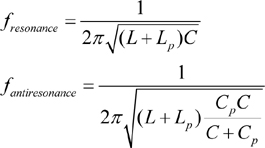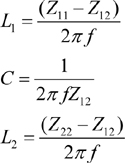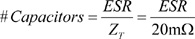This chapter is from the book
This chapter is from the book
This chapter is from the book
1.5 Analysis of PDNs
The impedance of a PDN is a parameter that can be calculated in the frequency domain through an AC analysis using a circuit simulator in which a 1-A current source is used as the excitation and the voltage at the various nodes of the system are calculated. The computed voltage represents either the self-impedance (voltage measured at the same node as the current excitation) or transfer impedance (voltage measured at a different node). Design of PDNs is always done in the frequency domain, and its analysis in the frequency domain therefore becomes very critical, as explained in the earlier discussion of target impedance. However, power supply noise is a time-domain event, and therefore, the computation of the noise in the time domain on the PDN is also important. Since the frequency response and time response are related to each other, the signature and amplitude of the time-domain response can be controlled by managing the impedance of the PDN in the frequency domain. This approach is very critical for the design of PDNs, since power supply noise in the time domain is a function of the slew rate (dI/dt) or, more generally, signature of the current excitation. In other words, different current signatures will always result in varying levels of power supply noise. Because it is difficult to excite all frequencies in the time domain (infinite current signatures would be necessary), a frequency domain analysis is preferable. The frequency domain analysis is explained in this section.
Consider the circuit representation of the PDN described earlier and shown in Figure 1-26. The impedances of such a network can be computed at any node or between any nodes. Two examples are shown in Figure 1-27. In Figure 1-27(a), the IC circuitry is removed, a 1-A current source is connected between the voltage and ground terminals of the IC, and the voltage at the same node is calculated as a function of frequency. Since a 1-A current source is used, the calculated voltage is the self-impedance (in ohms) seen by the IC looking down into the package toward the VRM. Similarly, in Figure 1-27(b), the board is analyzed separately where a current source of 1 A is connected across a board capacitor (e.g., by removing one of the capacitors in a measurement) and the voltage is measured across the same capacitor and also at the input end of the VRM across a bulk capacitor. The calculated voltage V1 is the self-impedance (in ohms), and voltage V2 is the transfer impedance (also in ohms), and both can be calculated as a function of frequency. Hence, the frequency domain analysis can be used to characterize any part of a PDN as long as the nodes in the network can be probed to connect the current source and measure the voltage. In practical measurements, this analysis is done using a vector network analyzer (VNA), where the S-parameters are measured as a function of frequency and can be transformed into impedances (explained in a later section).
){kind=link}
)
Figure 1-27 (a) Self-impedance seen by chip. (b) Self- and transfer impedance on board.
The role of the various components in a PDN is shown in Figure 1-28. The y-axis is the self-impedance at a node on the IC, and the x-axis is the frequency. At low kilohertz frequencies, the VRM and bulk capacitor impedance is low and begins to increase with a positive slope on the basis of the ESL of the bulk capacitors. In the megahertz frequencies, the capacitance of decoupling capacitors on the board reduces the impedance, thus producing a negative slope, which then becomes positive after the resonant frequency of the capacitors. The positive inductive slope caused by the ESL of the capacitors is then compensated by the plane capacitance, which pulls down the impedance through the negative slope shown in the figure up to several hundred megahertz. After the planes resonate, the frequency response of the planes becomes inductive and continues to have a positive slope into the gigahertz range, which is then compensated by the on-chip capacitance. As can be seen in the figure, the impedance fluctuates with multiple resonances (minimum impedance) and antiresonances (maximum impedance). Using the target impedance, the design goal is therefore to ensure that the impedance in Figure 1-28 does not exceed the target impedance at the desired frequencies, which can be for several hundreds of megahertz or several gigahertz.
)
Figure 1-28 Impedance versus frequency and the role of various components in the power delivery network. (Courtesy of Professor Juongho Kim, KAIST, South Korea, and Ansoft Corp.)
1.5.1 Single-Node Analysis
A single-node analysis is a simple analysis that can be done using a circuit simulator [7]. The assumption is that any variations in the voltage occur simultaneously across all of the PDN components, and therefore the separation between components is not critical. During the design of a PDN, the single-node analysis is the first step toward meeting the target impedance goals. By placing the VRM in parallel with all the decoupling capacitors, the number and value of the capacitors can be estimated to meet the target impedance goal.
Example
To illustrate single-node analysis, consider a plane pair (voltage plane above ground plane) of dimension 250 mm by 250 mm with a dielectric thickness of 0.2 mm. The dielectric constant is FR-4 with a relative permittivity of 4.0. In Figure 1-29, two ports are placed at positions P1 (1.25 mm, 126.25 mm) and P2 (248.75 mm,126.25 mm). P1 is the input port (current source), and P2 is the output port (voltage measurement). The plane pair is meshed with a unit cell size of 2.5mm (100 x 100 mesh) and solved using the multilayered finite difference method (M-FDM) described in detail in Chapter 2. The normalized differential voltage between the voltage and ground plane is shown in Figure 1-29(a) as a voltage distribution map at 30 MHz. As can be seen, except at the source, all unit cells are at the same voltage, implying the voltage distribution is constant along the entire surface of the plane. Hence, the plane pair behaves as a lumped capacitor at 30 MHz, and the nodes of any decoupling capacitors connected to these planes will all be at the same potential, irrespective of the capacitor position. The capacitance of the plane pair is 11.067 nF, and the magnitude of its impedance at 30 MHz is 0.479 W (1/[2p x 30 x 106 x 11.067 x 10-9]). Assuming a VRM of inductance 100 nH is connected to the plane at port P1, the impedance at port P2 is as shown in Figure 1-29(b). The antiresonance is caused by the parallel resonance between the inductance and the plane capacitance at approximately 4.78 MHz.
)
Figure 1-29 Single node analysis. (a) Voltage distribution on a plane pair at 30 MHz. (b) VRM + plane.
As explained earlier, when a capacitor is attached to a bare plane, it causes both a resonance and an antiresonance. For a capacitor with ESL = 2.53 nH and C = 100 nF, the resonance occurs at 10 MHz, while the antiresonance occurs at 31.7 MHz, according to equation (1.24). Both the resonance and antiresonance are shown in Figure 1-29(c). As can be seen from the figure, though the antiresonance is close to 31.7 MHz, there is a shift in resonance to a slightly lower frequency of approximately 30 MHz. This shift can be attributed to the plane inductance. Although the plane inductance is small compared to the ESL of the capacitor, it does have a small effect in shifting both the resonance and antiresonance frequencies. As the separation between the voltage and ground planes increases, the corresponding increase in the plane inductance causes a larger shift in the resonance and antiresonance frequencies. This shift is shown in Figure 1-29(d), where the antiresonance frequency for a capacitor with ESL = 2.53 nH and C = 100 nF mounted on a plane with dielectric separation from 0.05 mm to 0.4 mm is shown using equation (1.24) and the result of analysis using M-FDM. The error is 16% for a 0.4-mm separation and decreases to an error of 3% for a 0.05-mm separation. In Figure 1-29(d), the impedance is measured at port P2.
)
Figure 1-29 Single node analysis. (c) Capacitor with ESL = 2.53 nH and C = 100 nF mounted on plane. Via inductance is assumed to be included in the ESL of capacitor. (d) Antiresonance frequency versus plane separation based on equations (1.24) and (1.31).
With the plane inductance included, the resonance and antiresonance frequencies are modified as follows:
Equation 1.31
where L is the ESL of the capacitor, C is its capacitance, Lp is the plane inductance, and Cp is the plane capacitance.
1.5.1.1 Calculation of Plane Inductance at Low Frequencies
At low frequencies in the 1 to 50 MHz range, the plane can be represented using a lumped T-model, as shown in Figure 1-30(a) between ports P1 and P2. With a capacitor placed at port P1, the impedance seen at port P2 can be calculated. The T-model can be derived using a plane solver such as M-FDM by computing the two-port impedance between ports P1 and P2 at low frequencies. As an example, in Figure 1-29(a), the two-port Z-parameters at 10 MHz are Z11 = -j1.4122, Z12 = -j1.44089 and Z22 = -j1.4122. The inductance and capacitance of the T-model can then be derived from
Equation 1.32
)
Figure 1-30 (a) Equivalent circuit at low frequency (10 MHz) for capacitor mounted on plane with current source placed at port P1 and voltage measured at port P2. (b) Plane inductance vs. plane separation at 10 MHz.
leading to an inductance of 0.456 nH and capacitance of 11.04 nF. The variation of the inductance with plane separation for the structure in Figure 1-29(a) is shown in Figure 1-30(b), where the inductance increases almost linearly as the plane separation increases, as expected from equation (1.22).
1.5.1.2 Meeting Target Impedance at Frequencies below Cavity Resonance
Cavity resonance represents the frequencies at which the planes resonate, as described by equation (1.28). At frequencies below cavity resonance, the placement of capacitors is not critical and hence they can be uniformly distributed across the plane to meet the target impedance
As an example, let's assume that the target impedance required is 20 mW from DC to 30 MHz, which is not satisfied in Figure 1-29(b) because the impedance exceeds 20 mW for frequencies larger than 30 KHz. The goal is therefore to choose capacitors that resonate at frequencies at which the impedance must be reduced to meet the target impedance. As the capacitors are connected to the planes, antiresonances are created at frequencies given by equation (1.31), which we'll call LC antiresonance. The capacitors therefore have to be chosen such that they minimize the impedance at the antiresonance frequencies. The capacitors available to reach the 20-mW target impedance are shown in Table 1-2 along with their ESR, ESL, and resonant frequency values.
Table 1-2. Decoupling Capacitors
|
Capacitance (F) |
ESL (nH) |
ESR (mW) |
# of Capacitors |
Resonant Frequency (Hz) |
|
1.00 x 10-2 |
1 |
23 |
2 |
5.03 x 104 |
|
5.00 x 10-5 |
1 |
5 |
1 |
7.11 x 105 |
|
2.20 x 10-5 |
1 |
2 |
1 |
1.07 x 106 |
|
1.00 x 10-5 |
1 |
3.1 |
1 |
1.59 x 106 |
|
4.70 x 10-6 |
1 |
4.7 |
1 |
2.32 x 106 |
|
2.20 x 10-6 |
1 |
2.2 |
1 |
3.39 x 106 |
|
1.00 x 10-6 |
1 |
15.4 |
1 |
5.03 x 106 |
|
4.70 x 10-7 |
1 |
23.3 |
2 |
7.34 x 106 |
|
2.20 x 10-7 |
1 |
35.3 |
2 |
1.07 x 107 |
|
1.00 x 10-7 |
1 |
67.1 |
4 |
1.59 x 107 |
|
4.70 x 10-8 |
1 |
99.7 |
5 |
2.32 x 107 |
|
2.20 x 10-8 |
1 |
148.5 |
8 |
3.39 x 107 |
At the resonant frequency, the capacitor has the minimum impedance. Hence, the number of capacitors of each type required to meet the target impedance at the resonant frequency can be calculated using
Equation 1.33
Using equation (1.33), the number of each capacitor required is shown in Table 1-2. These capacitors can be placed and connected to the plane at any arbitrary position, since location does not matter. By connecting the capacitors in parallel in a circuit simulator, as shown in Figure 1-31(a), the impedance response similar to Figure 1-31(b) can be obtained. In Figure 1-31(a), multiple capacitors of the same type in parallel have been replaced with a single capacitor containing scaled values for ESR, ESL, and C. For example, two capacitors in parallel with C = 10 mF, ESL = 1 nH, and ESR = 23 mW have been replaced with a single capacitor with C' = 20 mF, ESL' = 0.5 nH, and ESR' = 11.5 mW without changing its resonant frequency. The impedance in Figure 1-31(b) was obtained using the M-FDM method in which the 20 mW target impedance is not exceeded up to 95 MHz. The inductive slope in Figure 1-31(b) is caused by the parallel combination of the ESL of all the capacitors. With 29 capacitors in parallel, each with an inductance of 1 nH, an equivalent inductance of 34.48 pH results, which corresponds to the impedance at ~100 MHz.
)
Figure 1-31 (a) Simple circuit model for connection of multiple capacitors (plane inductance not included). (b) VRM + plane + capacitors.
A practical example is shown in Figure 1-32 [7]: the VRM plus 144 capacitors of various types in parallel result in a frequency response that meets the target impedance up to 50 MHz. Beyond this frequency, the impedance becomes inductive (positive slope), as shown in the figure.
)
Figure 1-32 Single-node analysis to meet target impedance—a practical example. By permission from L.D. Smith, et al. [7], © 1999 IEEE.
1.5.2 Distributed Analysis
As the frequency extends beyond 50 MHz, the voltage distribution on the plane changes and standing waves are generated. From equation (1.28), a 250 mm by 250 mm plane resonates at 300 MHz (1,0 mode), 423 MHz (1,1 mode), 600 MHz (2,0 mode), 670 MHz (2,1 mode), 847 MHz (2,2 mode), 900 MHz (3,0 mode), and so on. A mode represents a voltage distribution. The voltage distribution for some of these resonant modes is shown in Figure 1-33; both the maximum voltage and minimum voltage are shown as a function of position on the planes. As can be seen, the plane is no longer an equipotential surface. At 300 MHz, a half wave stands along the length; at 600 MHz, a half wave stands along the length and width; at 670 MHz, a full wave stands along the width while a half wave stands along the length; and at 847 MHz, a full wave stands along the length and width. A full wave represents a standing wave with a 360-degree phase reversal, while a half wave represents a 180-degree phase reversal. For example, at 300 MHz, the maxima (plotted as magnitude) occurs at the near and far edge with a minima at the center, representing a 180-degree phase shift (phase not shown) and representing half of a standing wave. At frequencies at which the planes resonate, the location of the decoupling capacitors becomes important because they need to be located at a voltage maximum (or at the source) to reduce the bounce on the planes.
)
Figure 1-33 Voltage on planes (a) 300 MHz, (b) 600 MHz, (c) 670 MHz, and (d) 847 MHz.
Example
Consider Figure 1-33(a): the voltage peaks have to be reduced at 300 MHz. To monitor the voltage maximum, port 3 is placed at (7.5 mm, 7.5 mm). With a current source excitation of 1 A at port 1, the magnitude of the voltage measured at port 3 is plotted in Figure 1-34 as a function of frequency. An impedance peak can be seen at 300 MHz with an impedance magnitude of ~3 W. To reduce this peak, a capacitor with a resonant frequency of 300 MHz must be placed at (7.5 mm, 7.5 mm). The voltage distribution resulting from a capacitor with C = 1 nF, ESR = 10 mW, and ESL = 0.28 nH placed at (7.5 mm, 7.5 mm) is shown in Figure 1-35(a). Clearly, the voltage distribution on the plane changes with voltage minima occurring at the position where the capacitor is placed. The impedance at port
)
Figure 1-34 Transfer impedance between ports 1 and 3.
)
Figure 1-35 (a) Voltage distribution with capacitor, and (b) transfer impedance between ports 1 and 3.
3 with a current source excitation of 1 A at port 1 is plotted in Figure 1-35(b). The impedance peak of ~3 W has been reduced significantly. It is important to note that the placement of the capacitor at the center (125 mm, 125 mm) will not reduce the voltage variation on the plane at 300 MHz because, as per Figure 1-33(a), this represents a voltage minima point. Hence, the placement of the capacitors on the plane becomes very important, requiring a distributed analysis.
1.5.2.1 Meeting Target Impedance at Cavity Resonances
Meeting target impedance at cavity resonances is more tricky than at frequencies below cavity resonances because capacitors that resonate at higher frequencies are required. The principle of choosing the right capacitor and the number of capacitors required is similar to that of single-node analysis in which the capacitors are chosen such that they resonate at the cavity resonance frequency and the number of capacitors are chosen on the basis of equation (1.33). The primary difference is the placement of the capacitor.
In any computer system, the goal is always to minimize plane bounce, since any voltage variation on the planes can couple to signal lines referenced to it. To minimize voltage variations through the placement of capacitors, consider as an example the 250 mm by 250 mm plane described earlier. As before, the position of ports 1 and 2 remains the same. In addition, nine ports are uniformly added across the surface of the planes to monitor the voltage fluctuation. The source is at port 1, and the goal is to minimize the voltage fluctuations at the remaining ports. As discussed earlier, the first cavity resonance occurs at 300 MHz. Below this frequency, capacitors can be uniformly distributed using single-node analysis such that the target impedance is met. The transfer impedance between the source (port 1) and the remaining ports is shown in Figure 1-36(a), where the impedance of 20 mW has been met at most frequencies between DC and 300 MHz using single-node analysis and by uniformly distributing capacitors on the plane. Also shown is the first cavity resonance, which has shifted from the original frequency of 300 MHz to 340 MHz because of the loading of the planes by the ESL of the capacitors.
)
Figure 1-36 (a) Transfer impedance between ports. (b) Transfer impedance between ports with first cavity resonance suppressed.
At the cavity resonance of 340 MHz, the transfer impedance magnitude is not the same at the 11 ports. Hence, to reduce the impedance to meet target impedance, capacitors that resonate at 340 MHz have to be chosen with the number decided by equation (1.33). These capacitors have to be placed at the position next to where the transfer impedance needs to be reduced. The transfer impedances obtained by placing capacitors with ESR = 10 mW, ESL = 1 nH, and C = 0.219 nF next to the appropriate ports is shown in Figure 1-36(b), where the impedance at 340 MHz has been reduced. However, new antiresonances have been created near 280 MHz because of parallel resonance. The parallel resonance now must be reduced by using capacitors that resonate at 280 MHz.
Hence, the methodology for the placement of capacitors should include an initial single-node analysis followed by distributed analysis whereby the impedances are iteratively minimized across the plane surface to minimize plane bounce. This methodology can be extended to packages or boards containing multiple plane layers.