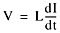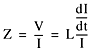- Describing Signal-Integrity Solutions in Terms of Impedance
- What Is Impedance?
- Real vs. Ideal Circuit Elements
- Impedance of an Ideal Resistor in the Time Domain
- Impedance of an Ideal Capacitor in the Time Domain
- Impedance of an Ideal Inductor in the Time Domain
- Impedance in the Frequency Domain
- Equivalent Electrical Circuit Models
- Circuit Theory and SPICE
- Introduction to Modeling
- The Bottom Line
This chapter is from the book
This chapter is from the book
This chapter is from the book
3.6 Impedance of an Ideal Inductor in the Time Domain
The behavior of an ideal inductor is defined by:
)
where:
-
V = the voltage across the inductor
-
L = the inductance of the inductor
-
I = the current through the inductor
This says that the voltage across an inductor depends on how fast the current through it changes. If the current is constant, the voltage across the inductor will be zero. Likewise, if the current changes rapidly through an inductor, there will be a large voltage drop across it. The inductance is the proportionality constant that says how sensitive the voltage generated is to a changing current. A large inductance means that a small changing current produces a large voltage.
There is often confusion about the direction of the voltage drop that is generated across an inductor. If the direction of the changing current reverses, the polarity of the induced voltage will reverse. An easy way of remembering the polarity of the voltage is to base it on the voltage drop of a resistor.
If a DC current goes through a resistor, the terminal the current goes into is the positive side and the other terminal is the negative side. Likewise, with an inductor, the terminal the current is increasing into is the positive side and the other is the negative side for the induced voltage. This is illustrated in Figure 3-6.
)
Figure 3-6. The direction of voltage drop across an inductor for a changing current is in the same direction as the voltage drop across
a resistor for a DC current.
Using this basic definition of inductance, we can calculate the impedance of an inductor. This is, by definition, the ratio of the voltage to the current through an inductor:
)
where:
-
V = the voltage across the inductor
-
L = the inductance of the inductor
-
I = the current through the inductor
Again, we see the impedance of an inductor, though well defined, is awkward to use in the time domain. The general features are easy to discern. If the current through an inductor increases rapidly, the impedance of the inductor is large. An inductor will have a high impedance when current through it tries to change. If the current through an inductor changes only slightly, its impedance will be very small. For DC current the impedance of an inductor is nearly zero. But, other than these simple generalities, the actual impedance of an inductor depends very strongly on the precise waveform of the current through it.
For both the capacitor and the inductor, the impedance, in the time domain, is not a simple function at all. Impedance in the time domain is a very complicated way of describing these basic building-block ideal circuit elements. It is not wrong, it is just complicated.
This is one of the important occasions where moving to the frequency domain will make the analysis of a problem much simpler.