- Describing Signal-Integrity Solutions in Terms of Impedance
- What Is Impedance?
- Real vs. Ideal Circuit Elements
- Impedance of an Ideal Resistor in the Time Domain
- Impedance of an Ideal Capacitor in the Time Domain
- Impedance of an Ideal Inductor in the Time Domain
- Impedance in the Frequency Domain
- Equivalent Electrical Circuit Models
- Circuit Theory and SPICE
- Introduction to Modeling
- The Bottom Line
This chapter is from the book
This chapter is from the book
This chapter is from the book
3.3 Real vs. Ideal Circuit Elements
There are two types of electrical devices, real and ideal. Real devices can be measured. They are the only things that physically exist. They are the actual interconnects or components that make up the hardware of a real system. Real devices are traces on a board, leads in a package, or discrete decoupling capacitors mounted to a board.
Ideal devices are mathematical descriptions of specialized circuit elements that have precise, specific definitions. Simulators can only simulate the performance of ideal devices. The formalism and power of circuit theory apply only to ideal devices. Models are composed of combinations of ideal devices.
It is very important to keep separate real versus ideal circuit elements. The impedance of any real, physical interconnect or passive component can be measured. However, when impedance is calculated, it is only the impedance of four very-well-defined, ideal circuit elements that can be considered. We cannot measure ideal circuit elements, nor can we calculate the impedance of any circuit elements other than ideal ones. This is why it is important to make the distinction between real components and ideal circuit elements. This distinction is illustrated in Figure 3-3.
)
Figure 3-3. The two worldviews of a component, in this case a 1206 decoupling capacitor mounted to a circuit board and an equivalent circuit
model composed of combinations of ideal circuit elements.
Ultimately, our goal is to create an equivalent circuit model composed of combinations of ideal circuit elements whose impedance closely approximates the actual, measured impedance of a real component.
A circuit model will always be an approximation of the real-world structure. However, it is possible to construct an ideal model with a simulated impedance which accurately matches the measured impedance of a real device. For example, Figure 3-4 shows the measured impedance of a real decoupling capacitor and the simulated impedance based on an RLC circuit model. These are the component and model in Figure 3-3. The agreement is excellent even up to 5 GHz, the bandwidth of the measurement.
)
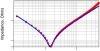Figure 3-4. The measured impedance, as circles, and the simulated impedance, as the line, for a nominal 1-nF decoupling capacitor. The
measurement was performed with a network analyzer and a GigaTest Labs Probe Station.
There are four ideal, two-terminal, circuit elements that we will use in combination as building blocks to describe any real interconnect:
-
A resistor
-
A capacitor
-
An inductor
-
A transmission line
We usually group the first three elements in a category called “lumped circuit elements,” in the sense that their properties can be lumped into a single point. This is different from the properties of an ideal transmission line, which are “distributed” along its length.
As ideal circuit elements, these elements have precise definitions that describe how they interact with currents and voltages. It is very important to keep in mind that ideal elements are different from real components, such as real resistors, real capacitors, or real inductors. One is a physical component, the other an ideal element.
The properties of a transmission line are initially seen as so confusing and non-intuitive, yet so important, that we devote an entire chapter to transmission lines and their impedance. In this chapter, we will concentrate on the impedance of just R, L, and C elements.
Only real devices can be measured, and only ideal elements can be calculated or simulated.
An equivalent electrical circuit model is an idealized electrical description of a real structure. It is an approximation, based on using combinations of ideal circuit elements. A good model will have a calculated impedance that closely matches the measured impedance of the real device. The better we can model the impedance of an interconnect, the better we can predict how a signal will interact with it.
When dealing with some high-frequency effects, such as lossy lines, we will need to invent new ideal circuit elements to create better models.