This is an excerpt from Algorithms, Part II, 4th Edition, which was published expressly to support the Coursera course, Algorithms: Part II.
For many sorting applications, the keys that define the order are strings. In this section, we look at methods that take advantage of special properties of strings to develop sorts for string keys that are more efficient than the general-purpose sorts that we considered in Chapter 2.
We consider two fundamentally different approaches to string sorting. Both of them are venerable methods that have served programmers well for many decades.
The first approach examines the characters in the keys in a right-to-left order. Such methods are generally referred to as least-significant-digit (LSD) string sorts. Use of the term digit instead of character traces back to the application of the same basic method to numbers of various types. Thinking of a string as a base-256 number, considering characters from right to left amounts to considering first the least significant digits. This approach is the method of choice for string-sorting applications where all the keys are the same length.
The second approach examines the characters in the keys in a left-to-right order, working with the most significant character first. These methods are generally referred to as most-significant-digit (MSD) string sorts—we will consider two such methods in this section. MSD string sorts are attractive because they can get a sorting job done without necessarily examining all of the input characters. MSD string sorts are similar to quicksort, because they partition the array to be sorted into independent pieces such that the sort is completed by recursively applying the same method to the subarrays. The difference is that MSD string sorts use just the first character of the sort key to do the partitioning, while quicksort uses comparisons that could involve examining the whole key. The first method that we consider creates a partition for each character value; the second always creates three partitions, for sort keys whose first character is less than, equal to, or greater than the partitioning key’s first character.
The number of characters in the alphabet is an important parameter when analyzing string sorts. Though we focus on extended ASCII strings (R = 256), we will also consider strings taken from much smaller alphabets (such as genomic sequences) and from much larger alphabets (such as the 65,536-character Unicode alphabet that is an international standard for encoding natural languages).
Key-indexed counting
As a warmup, we consider a simple method for sorting that is effective whenever the keys are small integers. This method, known as key-indexed counting, is useful in its own right and is also the basis for two of the three string sorts that we consider in this section.
Consider the following data-processing problem, which might be faced by a teacher maintaining grades for a class with students assigned to sections, which are numbered 1, 2, 3, and so forth. On some occasions, it is necessary to have the class listed by section. Since the section numbers are small integers, sorting by key-indexed counting is appropriate. To describe the method, we assume that the information is kept in an array a[] of items that each contain a name and a section number, that section numbers are integers between 0 and R-1, and that the code a[i].key() returns the section number for the indicated student. The method breaks down into four steps, which we describe in turn.
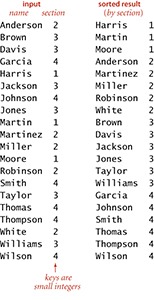
Figure 5.1 Typical candidate for key-indexed counting
Compute frequency counts.
The first step is to count the frequency of occurrence of each key value, using an int array count[]. For each item, we use the key to access an entry in count[] and increment that entry. If the key value is r, we increment count[r+1]. (Why +1? The reason for that will become clear in the next step.) In the example at left, we first increment count[3] because Anderson is in section 2, then we increment count[4] twice because Brown and Davis are in section 3, and so forth. Note that count[0] is always 0, and that count[1] is 0 in this example (no students are in section 0).
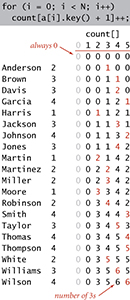
Figure 5.2 Computing frequency counts
Transform counts to indices.
Next, we use count[] to compute, for each key value, the starting index positions in the sorted order of items with that key. In our example, since there are three items with key 1 and five items with key 2, then the items with key 3 start at position 8 in the sorted array. In general, to get the starting index for items with any given key value we sum the frequency counts of smaller values. For each key value r, the sum of the counts for key values less than r+1 is equal to the sum of the counts for key values less than r plus count[r], so it is easy to proceed from left to right to transform count[] into an index table that we can use to sort the data.

Figure 5.3 Transforming counts to start indices
Distribute the data.
With the count[] array transformed into an index table, we accomplish the actual sort by moving the items to an auxiliary array aux[]. We move each item to the position in aux[] indicated by the count[] entry corresponding to its key, and then increment that entry to maintain the following invariant for count[]: for each key value r, count[r] is the index of the position in aux[] where the next item with key value r (if any) should be placed. This process produces a sorted result with one pass through the data, as illustrated at left. Note: In one of our applications, the fact that this implementation is stable is critical: items with equal keys are brought together but kept in the same relative order.
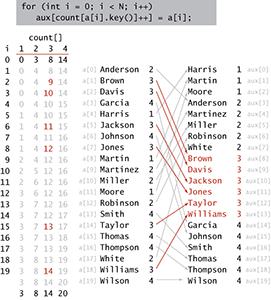
Figure 5.4 Distributing the data (records with key 3 highlighted)
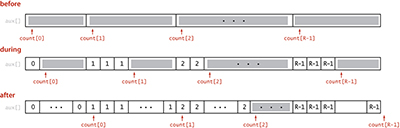
Figure 5.5 Key-indexed counting (distribution phase)
Copy back.
Since we accomplished the sort by moving the items to an auxiliary array, the last step is to copy the sorted result back to the original array.
Proposition A. Key-indexed counting uses 11N+4R+1 array accesses to stably sort N items whose keys are integers between 0 and R 2 1.
Proof: Immediate from the code. Initializing the arrays uses N 1 R 1 1 array accesses. The first loop increments a counter for each of the N items (2N array accesses); the second loop does R additions (2R array accesses); the third loop does N counter increments and Ndata moves (3N array accesses); and the fourth loop does N data moves (2N array accesses). Both moves preserve the relative order of equal keys.
Key-indexed counting is an extremely effective and often overlooked sorting method for applications where keys are small integers. Understanding how it works is a first step toward understanding string sorting. Proposition A implies that key-indexed counting breaks through the N log N lower bound that we proved for sorting. How does it manage to do so? Proposition I in SEction 2.2 is a lower bound on the number of compares needed (when data is accessed only through compareTo())—key-indexed counting does no compares (it accesses data only through key()). When R is within a constant factor of N, we have a linear-time sort.
int N = a.length; String[] aux = new String[N]; int[] count = new int[R+1]; // Compute frequency counts. for (int i = 0; i < N; i++) count[a[i].key() + 1]++; // Transform counts to indices. for (int r = 0; r < R; r++) count[r+1] += count[r]; // Distribute the records. for (int i = 0; i < N; i++) aux[count[a[i].key()]++] = a[i]; // Copy back. for (int i = 0; i < N; i++) a[i] = aux[i];
Key-indexed counting (a[].key is an int in [0, R).
