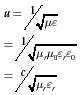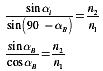Electro-Optics: Fundamentals of Light
Is optics an old or young topic? That question might start an endless debate. Some would argue "old," citing smoke signals as an example. Some would even list the creation, where God said, "Let there be light" (Genesis 1:3). Others might argue "young," citing laser and fiber optics or possibly semiconductor optical devices as proof. There are even newer disciplines such as acousto-optics, electro-optics, opto-electronics, and light-wave technology. Certainly some indicators of the newness of these technologies are the new terms evolving to describe the technologies. Terms like opto-electronics, photonics, and so forth are being coined and are not well defined. They do, however, indicate the mergers that are taking place between what used to be separate fields. So you might say that light is both an old and a young technology.
Introduction
Before we take a look at some specific newer technologies, let's discuss some fundamentals of light. Light has two aspects or natures, a wave nature and a particle nature.
First, the wave nature of light has the characteristics of frequency, phase, and velocity. Frequency and velocity are related by wavelength. That is,
(1.1)
where ![]() is the
velocity of light in a vacuum and
is the
velocity of light in a vacuum and
![]() is the wavelength in
free space in meters. In Chapter 4 we encounter the wave equation in a lossless
medium written
is the wavelength in
free space in meters. In Chapter 4 we encounter the wave equation in a lossless
medium written
(1.2)
where ![]() is the
electric field intensity,
is the
electric field intensity,
![]() is the permeability,
and
is the permeability,
and ![]() is permittivity.
If we specify E in the x direction and propagating in the z direction,
equation (1.2) becomes
is permittivity.
If we specify E in the x direction and propagating in the z direction,
equation (1.2) becomes
(1.3)
where the velocity is
(1.4)
where ![]() and
and
![]() . Equation (1.3) is
the wave equation. We then define a refractive index n, where
. Equation (1.3) is
the wave equation. We then define a refractive index n, where
(1.5)
Light travels more slowly in a medium when
![]() . That is,
. That is,
(1.6)
It is also shown in Chapter 4 that the wave equation can be written
(1.7)
where Hy is the magnetic field intensity in [A/m]. The electric and magnetic fields are related through the impedance. That is,
(1.8)
where ![]() is the
impedance in ohms. Optical intensity I is defined as optical power per
unit area. For example, from the preceding
is the
impedance in ohms. Optical intensity I is defined as optical power per
unit area. For example, from the preceding
(1.9)
and we can calculate optical power from
(1.10)
where ![]() is an area
normal to the direction of propagation,
is an area
normal to the direction of propagation,
![]() in the preceding
case.
in the preceding
case.
For a monochromatic (one color) wave, the electric field is written
(1.11)
where E0 is the amplitude,
![]() ,
,
![]() is the phase
constant, and z is the direction of propagation.
is the phase
constant, and z is the direction of propagation.
We summarize the wave nature of light by listing several equations that are basic to our study. The first four equations are called Maxwell's equations, credited to James Clerk Maxwell (1831-79), who put them together.
(1.12)
(1.13)
(1.14)
(1.15)
In addition there are two constitutive equations:
(1.16)
and
(1.17)
Equation (1.16) holds for electric fields in dielectrics, where
![]() is electric
polarization within the dielectric. Equation (1.17) holds for magnetic fields in
magnetic materials, where
is electric
polarization within the dielectric. Equation (1.17) holds for magnetic fields in
magnetic materials, where
![]() is the magnetic
polarization within the magnetic material.
is the magnetic
polarization within the magnetic material.
The particle nature of light states that light consists of light particles called photons. The energy of a photon is governed by Planck's constant or
(1.18)
where ![]() is
Planck's constant and f is frequency in Hz. The particle nature
implies that light travels according to ray or geometric optics. Ray optics
describes many experiments but is incomplete in describing others, for example,
diffraction.
is
Planck's constant and f is frequency in Hz. The particle nature
implies that light travels according to ray or geometric optics. Ray optics
describes many experiments but is incomplete in describing others, for example,
diffraction.
One of the more important laws in ray optics is Snell's law of reflection, which states that at a boundary the angle of incidence of a ray is equal to the angle of reflection. That is,
(1.19)
as shown in Figure 1-1. The incident wave reflects off the reflective surface
at an angle ![]() .
.
Figure 1-1 Snell's Law of Reflection.
Another law is Snell's law of refraction. That is,
(1.20)
as shown in Figure 1-2.
Figure 1-2 Snell's Law of Refraction.
The bending of the ray as it enters medium 2 from medium 1 depends on the ratio of the refractive indices in equation (1.20).
Referring back to equation (1.6) we see that the refractive index depends on ratio of the velocities of light in a vacuum to the speed of light in another medium.
(1.6)
Several indices of refraction are given in Table 1-1. Light of different frequencies refracts differently.
Table 1-1 Sampling of Refractive Indices
|
Medium |
|
|
Vacuum |
1.00 |
|
Acetone |
1.36 |
|
Fused quartz |
1.46 |
|
Glass |
1.52 |
|
Polystyrene |
1.55 |
|
Diamond |
2.42 |
Therefore, a light beam made up of several colors will refract differently at the boundary between two media. That is, the light travels along slightly different paths. This is called chromatic dispersion. A rainbow is an example of chromatic dispersion. To have chromatic dispersion, a light beam must have many colors. Two contrasting lights are an incandescent light beam and a laser light beam, for example. An incandescent light contains many colors or frequencies. It is called an incoherent light source. A laser light is monochromatic; it consists of one frequency or color (ideally). It is a coherent light source incident. Shown in Figure 1-3 is a prism with an incoherent light beam striking one side.
Figure 1-3 Prism with an Incoherent Light.
The light disperses into several rays, depending on wavelength, at two surfaces of the prism. The shorter wavelengths (higher frequencies) are on the bottom, and the larger wavelengths are toward the top of the prism. If in this example the light contained red and blue light, the upper ray would be red and the lower ray would be blue.
We next discuss total reflection.
In some situations it is possible that the light ray will not enter a second medium from the first. Consider the rays in Figure 1-4.
Figure 1-4 Reflections from an Air–Water Interface.
The swimmer under the water's surface views the surface from four
angles—![]() and
and
![]() . For ray 1,
. For ray 1,
![]() and some of the ray
is transmitted, some is reflected. For ray 2, some of the ray is transmitted;
more is reflected than for ray 1. As
and some of the ray
is transmitted, some is reflected. For ray 2, some of the ray is transmitted;
more is reflected than for ray 1. As
![]() increases, there is
an angle beyond which no ray is transmitted. That is the case for ray 3. There
is no transmitted ray; part of the ray travels along the boundary. The angle of
the transmitted ray is 90E. For ray 4, and all other rays that have an incident
angle greater than
increases, there is
an angle beyond which no ray is transmitted. That is the case for ray 3. There
is no transmitted ray; part of the ray travels along the boundary. The angle of
the transmitted ray is 90E. For ray 4, and all other rays that have an incident
angle greater than ![]() ,
there is total internal reflection. From equation (1.20) and using ray 3,
,
there is total internal reflection. From equation (1.20) and using ray 3,
where ![]() is the
refractive index of the water or
is the
refractive index of the water or
In general,
(1.21)
where ![]() is called
the critical angle. The swimmer in Figure 1-4 will not see any object above the
surface of the water for incident angles greater than
is called
the critical angle. The swimmer in Figure 1-4 will not see any object above the
surface of the water for incident angles greater than
![]() . There is total
internal reflection for
. There is total
internal reflection for
![]() . The critical angle
is important in fiber optics, in which case it is imperative that the light ray
stays in the fiber and not refract. More is said about that later.
. The critical angle
is important in fiber optics, in which case it is imperative that the light ray
stays in the fiber and not refract. More is said about that later.
Another angle of interest when considering reflection and refraction of light waves in dielectrics is the Brewster angle. Consider a light ray that is unpolarized as shown in Figure 1-5.
Figure 1-5 Parallel and Perpendicular Components.
By unpolarized we mean that the ray contains both perpendicular and parallel components of the electric field vector. The words perpendicular and parallel are with reference to the plane of incidence. The plane of incidence is the plane of the page; it contains the incident, reflected, and refracted rays. We can see in Figure 1-5 that the incident ray contains both components but the reflected ray contains only the perpendicular component. In addition, the refracted ray contains both components. Thus, the reflected ray has become polarized.
It is an experimental fact that the sum of the reflected and refracted angles
is 90E. Since ![]() ,
then
,
then
(1.22)
From equation (1.20)
(1.20)
where ![]() is the
medium that contains the incident ray. Substituting (1.22) into (1.20) andnoting
that
is the
medium that contains the incident ray. Substituting (1.22) into (1.20) andnoting
that ![]() , we obtain
, we obtain
and
(1.23)
where ![]() is the
Brewster angle. If medium 1 is air, then equation (1.23) becomes
is the
Brewster angle. If medium 1 is air, then equation (1.23) becomes
(1.24)
where ![]() is the
refractive index of the second medium. Equation (1.24) is Brewster's
law.
is the
refractive index of the second medium. Equation (1.24) is Brewster's
law.