- What Is Analytics?
- Why Is Analytics Important in Project Management?
- How Can Project Managers Use Analytics in Project Management?
- Project Management Analytics Approach
- Summary
- Key Terms
- Case Study: City of Medville Uses Statistical Approach to Estimate Costs for Its Pilot Project
- Case Study Questions
- Chapter Review and Discussion Questions
- Bibliography
Project Management Analytics Approach
The project management analytics approach can vary from organization to organization and even from project to project. It depends on multiple factors including, but not limited to, organizational culture; policies and procedures; project environment; project complexity; project size; available resources; available tools and technologies; and the skills, knowledge, and experience of the project manager or project/business analysts. This book covers the following approaches to project management analytics:
- Statistical
- Lean Six Sigma
- Analytic Hierarchy Process
You will look at the application of each of these approaches and the possible combination of two or more of these approaches, depending upon the project characteristics.
Statistical Approach
“Lies, damned lies, and statistics!
Nothing in progression can rest on its original plan.”
- —Thomas S. Monson (American religious leader and author)
Throughout the project life cycle, project managers must deal with a large number of uncertainties. For instance, project risks are uncertainties that can derail the project if they are not addressed in a timely and effective way. Similarly, all project baselines (plans) are developed to deal with the uncertain future of the project. That’s why the project plans are called living documents because they are subject to change based on future changes. Because picturing the future precisely is hard, best estimates are used to develop the project plans.
Statistical approach comes in handy when dealing with project uncertainties because it includes tools and techniques that managers can deploy to interpret specific patterns in the data pertaining to the project management processes to predict the future more accurately.
Quantitative measure of a process, when that process is performed over and over, is likely to follow a certain frequency pattern of occurrence. In other words, there is a likelihood or probability of recurrence of the same quantitative measure in the long run. This likelihood or probability represents the uncertainty of recurrence of a certain quantitative value of the process. Statistical analysis can help predict certain behaviors of the processes or systems in the environment of uncertainty, which is fundamental to data-driven decision-making.
We use the following analytical probability distributions to illustrate how a statistical approach can help in effective decision-making in project management:
- Normal distribution
- Poisson distribution
- Uniform distribution
- Triangular distribution
- Beta distribution
Normal Distribution
Depicted in Figure 1.2, the normal distribution is the most common form of the probability density function. Due to its shape, it is also referred to as the bell curve. In this distribution, all data values are symmetrically distributed around the mean of the probability. The normal distribution method constitutes a significant portion of the statistical content that this book covers because the project management processes involve a number of normal events.8
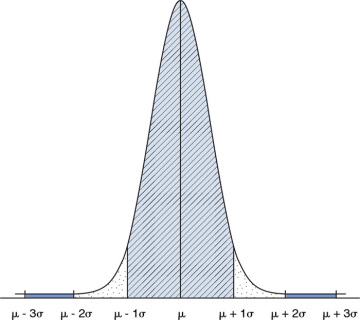
Figure 1.2 Normal Distribution
Normal distribution is the result of the process of accumulation. Usually, the sum or average of the outcomes of various uncertainties constitutes an outcome whose probability distribution is a normal distribution.
For data with a normal distribution, the standard deviation has the following characteristics:9
- 68.27% of the data values lie within one standard deviation of the mean.
- 95.45% of the data values lie within two standard deviations of the mean.
- 99.73% of the data values lie within three standard deviations of the mean.
Poisson Distribution
Poisson distribution is the result of the process of counting. Figure 1.3 depicts the shape of a typical Poisson distribution curve.
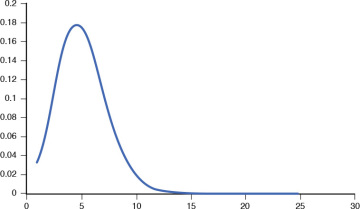
Figure 1.3 Poisson Distribution
This distribution can be used to count the number of successes or opportunities as a result of multiple tries within a certain time period. For example, it can be used to count
- The number of projects human resources acquired in a period of two months
- The number of project milestones completed in a month
- The number of project tasks completed in a given week
- The number of project change requests processed in a given month
Chapter 4, “Statistical Fundamentals I,” covers the Poisson distribution in more depth and examines how this distribution can be used in project management to count discrete,10 countable, independent events.
Uniform Distribution
Illustrated in Figure 1.4, a uniform distribution is also referred to as a rectangular distribution with constant probability.
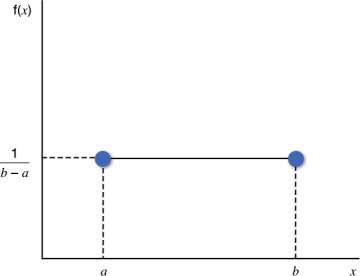
Figure 1.4 Uniform Distribution
The area of the rectangle is equal to the product of its length and its width.
Thus, the area of the rectangle equals (b – a) * 1/ (b – a) = 1.
What does this mean? This means that for a continuous11 random variable, the area under the curve is equal to 1. This is true in the case of a discrete random variable as well provided the values of the discrete random variable are close enough to appear almost continuous.
The unit area under the curve in Figure 1.4 illustrates that relative frequencies or probabilities of occurrence of all values of the random variable, when integrated, are equal to 1. That is:
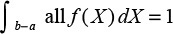
In this equation, dX is an increment along the x-axis and f(X) is a value on the y-axis.
Uniform distribution arbitrarily determines a two-point estimate of the highest and lowest values (endpoints of a range) of a random variable. This simplest estimation method allows project managers to transform subjective data into probability distributions for better decision-making especially in risk management.
Triangular Distribution
Unlike uniform distribution, the triangular distribution illustrates that the probability of all values of a random variable are not uniform. Figure 1.5 shows the shape of a triangular distribution.
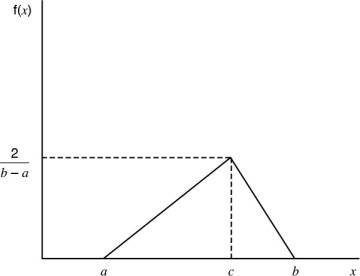
Figure 1.5 Triangular Distribution
A triangular distribution is called so because of its triangular shape. It is based on three underlying values: a (minimum value), b (maximum value), and c (peak value) and can be used estimate the minimum, maximum, and most likely values of the outcome. It is also called three-point estimation, which is ideal to estimate the cost and duration associated with the project activities more accurately by considering the optimistic, pessimistic, and realistic values of the random variable (cost or duration). The skewed nature of this distribution represents the imbalance in the optimistic and pessimistic values in an event. Like all probability density functions, triangular distribution also has the property that the area under the curve is 1.
Beta Distribution
The beta distribution depends on two parameters—α and β where α determines the center or steepness of the hump of the curve and β determines the shape and fatness of the tail of the curve. Figure 1.6 shows the shape of a beta distribution.
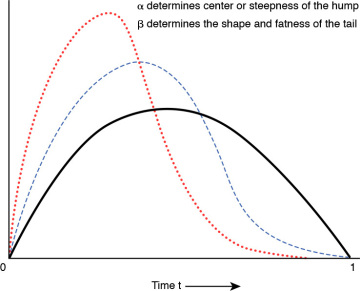
Figure 1.6 Beta Distribution
Like triangular distribution, beta distribution is also useful in project management to model the events that occur within an interval bounded by maximum and minimum end values. You will learn how to use this distribution in PERT (Program Evaluation and Review Technique) and CPM (Critical Path Method) for three-point estimation in Chapter 8.
Lean Six Sigma Approach
The Lean12 Six Sigma13 approach encompasses reduction in waste and reduction in variation (inaccuracy). For decisions to be rational and effective, they should be based on an approach that promotes these things. That is the rationale behind the use of the Lean Six Sigma approach in project management analytics.
The goal of every project organization in terms of project outcome is SUCCESS, which stands for
- SMART14 Goals Established and Achieved
- Under Budget Delivered Outcome
- Communications Effectiveness Realized
- Core Values Practiced
- Excellence in Project Management Achieved
- Schedule Optimized to Shorten Time to Delivery
- Scope Delivered as Committed
The projects are typically undertaken to improve the status quo of a certain prevailing condition, which might include an altogether missing functionality or broken functionality. This improvement effort involves defining the current (existing) and the target conditions, performing gap analysis (delta between the target and the current condition), and understanding what needs to be done to improve the status quo. The change from the current condition to the target condition needs to be managed through effective change management. Change management is an integral part of project management and the Lean Six Sigma approach is an excellent vehicle to implement changes successfully.
The DMAIC Cycle
Like the project management life cycle, Lean Six Sigma also has its own life cycle called the DMAIC cycle. DMAIC stands for the following stages of the Lean Six Sigma life cycle:
- Define
- Measure
- Analyze
- Improve
- Control
The DMAIC is a data-driven process improvement, optimization, and stabilization cycle. All stages of the DMAIC cycle are mandatory and must be performed in the order from “define” to “control.” Figure 1.7 depicts a typical DMAIC cycle.

Figure 1.7 DMAIC Cycle
The various stages of the DMAIC cycle are briefly described here (refer to Chapter 7, “Lean Six Sigma,” for detailed discussion on the DMAIC cycle):
- Define: Define the problem and customer requirements.
- Measure: Measure the current performance of the process (establish baseline), determine the future desired performance of the process (determine target), and perform gap analysis (target minus baseline).
- Analyze: Analyze observed and/or measured data and find root cause(s). Modify the process if necessary but re-baseline the performance post-modification.
- Improve: Address the root cause(s) to improve the process.
- Control: Control the future performance variations.
The PDSA Cycle
Project quality is an integral part of project management. The knowledge of Lean Six Sigma tools and processes arms a project manager with the complementary and essential skills for effective project management. The core of Lean Six Sigma methodology is the iterative PDSA (Plan, Do, Study, Act) cycle, which is a very structured approach to eliminating or minimizing defects and waste from any process.
Figure 1.8 shows the PDSA cycle. We discuss this cycle as part of our discussion on the applications of the Lean Six Sigma approach in project management.
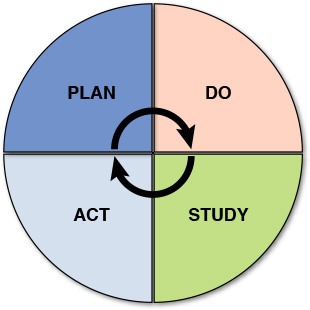
Figure 1.8 PDSA Cycle
Brief explanations of the building blocks of the PDSA cycle follow (refer to Chapter 7 for detailed discussion on the PDSA cycle):
- Plan: The development of the plan to carry out the cycle
- Do: The execution of the plan and documentation of the observations
- Study: The analysis of the observed and collected data during the execution of the PDSA plan
- Act: The next steps based on the analysis results obtained during study
Lean Six Sigma Tools
The Lean Six Sigma processes involve a lot of data collection and analysis. The various tools used for this purpose include the following:
- Brainstorming: To collect mass ideas on potential root causes
- Surveys: To collect views of the individuals who are large in number and/or outside personal reach
- Five whys: A method that asks five probing questions to identify the root cause
- Value stream mapping: Process map analysis to identify wasteful process steps
- Cause and effect or fishbone or Ishikawa diagram: A tool to help with brainstorming on the possible root causes
- Control charts: To identify “common” and “special” causes in the stream of data observed over a period of time
- Correlation: To study the correlation between two variables
- Cost-benefits analysis: To estimate the cost of implementing an improvement plan and the benefits realized
- Design of experiments: To identify the recipe for the best possible solution
- Histograms: Unordered frequency (of defects) map
- Pareto charts: Ordered (descending) frequency (of defects) map
- Regression analysis: To study the effect of one variable with all other variables held constant
- Root cause analysis: Analysis to find the “cure” for a problem rather than just “symptoms treatment”
- Run charts: Observed data over a period of time
- SIPOC15 chart: Process analysis to identify input and output interfaces to the process
These tools are discussed in more detail in Chapter 7.
How Can You Use the Lean Six Sigma Approach in Project Management?
We will examine a hybrid approach by blending the DMAIC cycle with the project management life cycle, which project managers can use to find the root cause(s) of the following project path holes and recommend the appropriate corrective actions to fix them.
- Schedule delays
- Project scope creep
- Cost overruns
- Poor quality deliverables
- Process variation
- Stakeholder dissatisfaction
Analytic Hierarchy Process (AHP) Approach
Proposed by Thomas L. Saaty in 1980, the AHP is a popular and effective approach to multi-criteria-driven decision-making. According to Saaty, both tangible and intangible factors should be considered while making decisions. “Decisions involve many intangibles that need to be traded off. To do that, they have to be measured alongside tangibles whose measurements must also be evaluated as to how well they serve the objectives of the decision maker,” says Saaty.
You can use the AHP approach in any scenario that includes multiple factors in decision-making. For example:
- Deciding which major to select after high school
- Deciding which university to select after high school
- Deciding which car to select for buying
- Deciding which projects to select for inclusion in the portfolio
Often in decision-making, the intangible factors are either overlooked or the decisions are just made based on subjective or intuitional criteria alone. The AHP approach is a 360® approach, which includes both subjective and objective criteria in decision-making. The key characteristic of this approach is that it uses pairwise comparisons16 of all the possible factors of the complex problem at hand and evaluates their relative importance to the decision-making process. For example, project management decision-making criteria may include three factors: schedule flexibility, budget flexibility, and scope flexibility. To make a decision, the project manager must consider the relative importance of each of the three factors against every other factor in the criteria. Schedule, budget, and scope are the triple constraints of project management and a tradeoff often has to be made to find the right balance among them based on the business need and/or the project environment. For instance, less flexibility in scope requires schedule, budget, or both to be relatively more flexible.
Chapter 6 covers the AHP approach in more detail. This book makes extensive use of this approach in recommending data-driven methodology for making the most effective and rational project management decisions, including the following:
- Project selection and prioritization
- Project risk identification and assessment
- Selection of project risk response strategy
- Vendor selection
- Project resource allocation optimization
- Project procurement management
- Project quality evaluation