Sports Analytics and Data Science: Understanding Sports Markets

This chapter is from the book

Sports Analytics and Data Science: Winning the Game with Methods and Models

Learn More Buy

This chapter is from the book

This chapter is from the book 

Sports Analytics and Data Science: Winning the Game with Methods and Models

Learn More Buy

• “Those of you on the floor at the end of the game, I’m proud of you. You played your guts out. I’m only going to say this one time. All of you have the weekend. Think about whether or not you want to be on this team under the following condition: What I say when it comes to this basketball team is the law, absolutely and without discussion.”
• —GENE HACKMAN AS COACH NORMAN DALE IN Hoosiers (1986)

In applying the laws of economics to professional sports, we must consider the nature of sports and the motives of owners. Professional sports are different from other forms of business.

There are sellers and buyers of sports entertainment. The sellers are the players and teams within the leagues of professional sports. The buyers are consumers of sports, many of whom never go to games in person but who watch sports on television, listen to the radio, and buy sports team paraphernalia.

Sports compete with other forms of entertainment for people’s time and money. And various sports compete with one another, especially when their seasons overlap. Sports teams produce entertainment content that is distributed through the media. Sports teams license their brand names and logos to other organizations, including sports apparel manufacturers.

Sports teams are not independent businesses competing with one another. While players and teams compete on the fields and courts of play, they cooperate with one another as members of leagues. The core product of sports is the sporting contest, a joint product of two or more players or two or more teams.

Fifty-four sports and recreation activities, shown in table 1.1, are tracked by the National Sporting Goods Association (2015), which serves the sporting goods industry. In recent years, participation in baseball, basketball, football, and tennis has declined, while participation in soccer has increased. There has been growth in individual recreational sports, such as skateboarding and snowboarding. Of course, levels of participation in sports are not necessarily an indicator of levels of interest in sports as entertainment.

Table 1.1. Sports and Recreation Activities in the United States

Sports businesses produce entertainment products by cooperating with one another. While it is illegal for businesses in most industries to collude in setting output and prices, sports leagues engage in cooperative output and pricing as a standard part of their business model. The number of games, indeed the entire schedule of games in a sport, is determined by the league. In fact, aspects of professional sports are granted monopoly power by the federal government in the United States.

When developing a model for a typical business or firm, an economist would assume profit maximization as a motive. But for a professional sports team, an owner’s motives may not be so easily understood. While one owner may operate his or her team for profit year by year, another may seek to maximize wins or overall utility. Another may look for capital appreciation—buying, then selling after a few years. Lacking knowledge of owners’ motives, it is difficult to predict what they will do.

Gaining market share and becoming the dominant player is a goal of firms in many industries. Not so in the business of professional sports. If one team were assured of victory in almost all of its contests, interest in those contests could wane. A team benefits by winning more often than losing, but winning all the time may be less beneficial than winning most of the time. Professional sports leagues claim to be seeking competitive balance, although there are dominant teams in many leagues.

Sports is big business as shown by valuations and finances of the major professional sports in the United States and worldwide. Data from Forbes for Major League Baseball (MLB), the National Basketball Association (NBA), the National Football League (NFL), and worldwide soccer teams are shown in tables 1.2 through 1.5.

Table 1.2. MLB Team Valuation and Finances (March 2015)

Table 1.3. NBA Team Valuation and Finances (January 2015)

Table 1.4. NFL Team Valuation and Finances (August 2014)

Table 1.5. World Soccer Team Valuation and Finances (May 2015)

Professional sports teams most certainly compete with one another in the labor market, and labor in the form of star players is in short supply. Some argue that salary caps are necessary to preserve competitive balance. Salary caps also help teams in limiting expenditures on players.

Most professional sports in the United States have salary caps. The 2015 salary cap for NFL teams, with fifty-three player rosters, is set at $143.28 million (Patra 2015). Most teams have payrolls at or near the cap, making the average salary of an NFL player about $2.7 million. One player on an NFL team may be designated as a franchise player, restricting that player from entering free agency. The league sets minimum salaries for franchise players. For example, a franchise quarterback has a minimum salary of $18.544 million in 2015. The highest annual salary among NFL players is $22 million for Aaron Rodgers, Green Bay Packers quarterback (spotrac 2015c). The minimum annual salary is $420 thousand.

NBA teams have a $70 million salary cap for the 2015–16 season, with penalties for teams going over the cap. Maximum player salaries are based on a percentage of cap and years of service. For example, LeBron James, with ten years of experience, would have a maximum salary of $23 million (Mahoney 2015). New Orleans Pelicans Anthony Davis’ average salary of $29 million is the highest among NBA players (spotrac 2015b). Team rosters include fifteen players under contract, with as many as thirteen available to play in any particular game. The minimum annual salary is $428,498.

Major League Baseball (MLB) has a “luxury tax” for teams with payrolls in excess of $189 million. There is a regular-player roster of twenty-five or twenty-six players for double-header days/nights. A forty-man roster includes players under contract and eligible to play. Between September 1 and the end of the regular season the roster is expanded to forty players. The roster drops back to twenty-five players for the playoffs. The minimum MLB annual salary is $505,700 in 2015. The highest MLB annual salary is $31 million for Miguel Cabrera of the Detroit Tigers (spotrac 2015a).

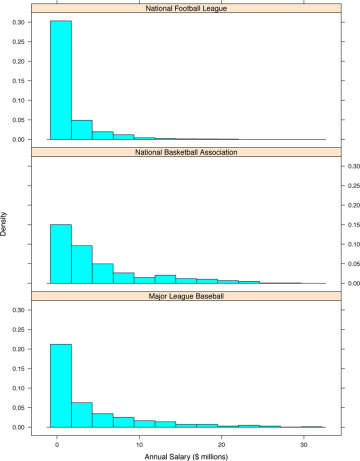
Figure 1.1, a histogram lattice, shows how player salaries compare across the MLB, NBA, and NFL in August 2015. Player salary distributions are positively skewed. The mean salary across NFL players is around $1.7 million, but the median is $630 thousand. The mean salary across NBA players is around $5.1 million, with median salary $2.8 million. The mean salary across MLB players is around $4.1 million, with the median $1.1 million.

Figure 1.1. MLB, NBA, and NFL Average Annual Salaries

Sources. spotrac (2015a, 2015b, 2015c).

Do team expenditures on players buy success? This is a meaningful question to ask for leagues that have no salary caps. Szymanski (2015) reports studies showing that between 60 and 90 percent of the variability in U.K. soccer team positions may be explained by wages paid to players. Major League Baseball has a luxury tax in place of a salary cap, and team payrolls vary widely in size. The New York Yankees have been known for having the highest payrolls in baseball. Recently, the Los Angeles Dodgers have surpassed the Yankees with the highest player payroll—more than $257 million at the end of the 2014 season (Woody 2014).

Figure 1.2 shows baseball team salaries at the beginning of the 2014 season plotted against the percentage of games won across the regular season. Notice how teams that made the playoffs in 2014, labeled with team abbreviations, have a wide range of payrolls. While the biggest spenders in baseball are often among the set of teams going to the playoffs, the relationship between team payrolls and team performance is weak at best—less than 7 percent of the variability in win/loss percentages is explained by player payrolls.

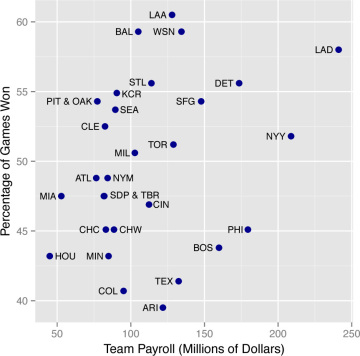
Figure 1.2. MLB Team Payrolls and Win/Loss Performance (2014 Season)

Sources. Sports Reference LLC (2015b) and USA Today (2015).

See Appendix B, page 255, for team abbreviations and names.

The thesis of Michael Lewis’ Moneyball (2003) and what has become the ethos of sports analytics is that small-market baseball teams can win by spending their money wisely. Star players demand top salaries due as much to their celebrity status as to their skills. Players with high on-base percentages, overlooked by major-market teams, can be hired at much lower salaries than star players.

Teams, although associated with particular cities, can be known nationwide or worldwide. The media of television and the Internet provide opportunities for reaching consumers across the globe. A Super Bowl at the Rose Bowl in Pasadena, California or AT&T Stadium in Arlington, Texas may be attended by around 100 thousand fans (Alder 2015), while U.S. television audiences have grown to over 100 million (statista 2015).

Media revenues are important to successful sports teams. Other revenues come from business partnerships, sponsorships, advertising, and stadium naming rights. City governments understand well the power of sports to promote business. Locating sports arenas in cities can help to revitalize downtown areas, as demonstrated by the experience of the Oklahoma City Thunder. Indianapolis, Indiana promotes itself as a sports capital with the Colts and Pacers (Rein, Shields, and Grossman 2015).

Teams seek to build their brands, developing a positive reputation in the minds of consumers. Players, like fans, are attracted to teams with a reputation for hard work, courage, fair play, honesty, teamwork, and community service. The character of a team is often as important as its likelihood of winning. The Cubs are associated with Chicago, but Cub fans may be found from Maine to California. This is despite the fact that the Cubs have not won the World Series since 1908. Teams in U.S. professional sports vie to become “America’s team,” with fans across the land wearing their logoembossed hats and jerseys.

The demand for sports and the feelings of sports consumers are not so easily understood. Fans can be fickle and fandom fleeting. Fans can be loyal to a sport, to a team, or to individual players. Multivariate methods can help us understand how sports consumers think by revealing relationships among products or brands.

Figure 1.3 provides an example, a perceptual map of seven sports. Along the horizontal dimension, we move from individual, non-contact sports on the left-hand side, to team sports with little contact, to team sports with contact on the right-hand side. The vertical dimension, less easily described, may be thought of as relating to the aerobic versus anaerobic nature of sports and to other characteristics such as physicality and skill. Sports such as tennis, soccer, and basketball entail aerobic exercise. These are endurance sports, while football is an example of a sport that involves both aerobic and anaerobic exercise, including intense exercise for short durations. Sports close together on the map have similarities. Baseball and golf, for example, involve special skills, such as precision in hitting a ball. Soccer and hockey involve almost continuous movement and getting a ball through the goal. Football and hockey have high physicality or player contact.

Figure 1.3. A Perceptual Map of Seven Sports

In many respects, professional sports teams are decidedly different from other businesses. They are in the public eye. They live and die in the media. And a substantial portion of their revenues come from media.

Késenne (2007), Szymanski (2009), Fort (2011), Fort and Winfree (2013), Leeds and von Allmen (2014), and the edited volumes of Humphreys and Howard (2008a, 2008b, 2008c) review sports economics and business issues.

Gorman and Calhoun (1994) and Rein, Shields, and Grossman (2015) focus on alternative sources of revenue for sports teams and how these relate to business strategy. The business of baseball has been the subject of numerous volumes (Miller 1990; Zimbalist 1992; Powers 2003; Bradbury 2007; Pessah 2015). And Jozsa (2010) reviews the history of the National Basketball Association.

An overview of sports marketing is provided by Mullin, Hardy, and Sutton (2014). Rein, Kotler, and Shields (2006) and Carter (2011) discuss the convergence of entertainment and sports. Miller (2015a) reviews methods in marketing data science, including product positioning maps, market segmentation, target marketing, customer relationship management, and competitive analysis.

Sports also represents a laboratory for labor market research. Sports is one of the few industries in which job performance and compensation are public knowledge. Economic studies examine player performance measures and value of individual players to teams (Kahn 2000; Bradbury 2007). Miller (1991), Abrams (2010), and Lowenfish (2010) review baseball labor relations. And Early (2011) provides insight into labor and racial discrimination in professional sports.

Sports wagering markets have been studied extensively by economists because they provide public information about price, volume, and rates of return. Furthermore, sports betting opportunities have fixed beginning and ending times and published odds or point spreads, making them easier to study than many financial investment opportunities. As a result, sports wagering markets have become a virtual field laboratory for the study of market efficiency. Sauer (1998) provides a comprehensive review of the economics of wagering markets.

When management objectives can be defined clearly in mathematical terms, teams use mathematical programming methods—constrained optimization. Teams attempt to maximize revenue or minimize costs subject to known situational factors. There has been extensive work on league schedules, for which the league objective may be to have teams playing one another an equal number of times while minimizing total distance traveled between cities. Alternatively, league officials may seek home/away schedules, revenue sharing formulas, or draft lottery rules that maximize competitive balance. Briskorn (2008) reviews methods for scheduling sports competition, drawing on integer programming, combinatorics, and graph theory. Wright (2009) provides an overview of operations research in sport.

Extensive data about sports are in the public domain, readily available in newspapers and online sources. These data offer opportunities for predictive modeling and research. Throughout the book we also identify places to apply methods of operations research, including mathematical programming and simulation.

Exhibit 1.1 shows an R program for exploring distributions of player salaries across the MLB, NBA, and NFL. The program draws on software for statistical graphics from Sarkar (2008).

Exhibit 1.2 (page 18) shows an R program for examining the relationship between MLB payrolls and win-loss performance. The program draws on software for statistical graphics from Wickham and Chang (2014).

Exhibit 1.3 (page 19) shows an R program to obtain a perceptual map of seven sports, showing their relationships with one another. The program draws on modeling software for multidimensional scaling.

Exhibit 1.1. MLB, NBA, and NFL Player Salaries (R)

# MLB, NBA, and NFL Player Salaries (R)

library(lattice)  # statistical graphics

# variables in contract data from spotrac.com (August 2015)
#   player: player name (contract years)
#   position: position on team
#   team: team abbreviation
#   teamsignedwith: team that signed the original contract
#   age: age in years as of August 2015
#   years:  years as player in league
#   contract: dollars in contract
#   guaranteed: guaranteed dollars in contract
#   guaranteedpct: percentage of contract dollars guaranteed
#   salary: annual salary in dollares
#   yearfreeagent: year player becomes free agent
#
#   additional created variables
#   salarymm: salary in millions
#   leaguename: full league name
#   league: league abbreviation

# read data for Major League Baseball
mlb_contract_data <- read.csv("mlb_player_salaries_2015.csv")
mlb_contract_data$leaguename <- rep("Major League Baseball",
    length = nrow(mlb_contract_data))
for (i in seq(along = mlb_contract_data$yearfreeagent))
    if (mlb_contract_data$yearfreeagent[i] == 0)
        mlb_contract_data$yearfreeagent[i] <- NA
for (i in seq(along = mlb_contract_data$age))
    if (mlb_contract_data$age[i] == 0)
        mlb_contract_data$age[i] <- NA
mlb_contract_data$salarymm <- mlb_contract_data$salary/1000000
mlb_contract_data$league <- rep("MLB", length = nrow(mlb_contract_data))
print(summary(mlb_contract_data))
# variables for plotting
mlb_data_plot <- mlb_contract_data[, c("salarymm","leaguename")]

nba_contract_data <- read.csv("nba_player_salaries_2015.csv")
nba_contract_data$leaguename <- rep("National Basketball Association",
    length = nrow(nba_contract_data))
for (i in seq(along = nba_contract_data$yearfreeagent))
    if (nba_contract_data$yearfreeagent[i] == 0)
        nba_contract_data$yearfreeagent[i] <- NA
for (i in seq(along = nba_contract_data$age))
    if (nba_contract_data$age[i] == 0)
        nba_contract_data$age[i] <- NA
nba_contract_data$salarymm <- nba_contract_data$salary/1000000
nba_contract_data$league <- rep("NBA", length = nrow(nba_contract_data))
print(summary(nba_contract_data))
# variables for plotting
nba_data_plot <- nba_contract_data[, c("salarymm","leaguename")]

nfl_contract_data <- read.csv("nfl_player_salaries_2015.csv")
nfl_contract_data$leaguename <- rep("National Football League",
    length = nrow(nfl_contract_data))
for (i in seq(along = nfl_contract_data$yearfreeagent))
    if (nfl_contract_data$yearfreeagent[i] == 0)
        nfl_contract_data$yearfreeagent[i] <- NA
for (i in seq(along = nfl_contract_data$age))
    if (nfl_contract_data$age[i] == 0)
        nfl_contract_data$age[i] <- NA
nfl_contract_data$salarymm <- nfl_contract_data$salary/1000000
nfl_contract_data$league <- rep("NFL", length = nrow(nfl_contract_data))
print(summary(nfl_contract_data))
# variables for plotting
nfl_data_plot <- nfl_contract_data[, c("salarymm","leaguename")]

# merge contract data with variables for plotting
plotting_data_frame <- rbind(mlb_data_plot, nba_data_plot, nfl_data_plot)

# generate the histogram lattice for comparing player salaries
# across the three leagues in this study
lattice_object <- histogram(~salarymm | leaguename, plotting_data_frame,
    type = "density", xlab = "Annual Salary ($ millions)", layout = c(1,3))

# print to file
pdf(file = "fig_understanding_markets_player_salaries.pdf",
     width = 8.5, height = 11)
print(lattice_object)
dev.off()

Exhibit 1.2. Payroll and Performance in Major League Baseball (R)

# Payroll and Performance in Major League Baseball (R)

library(ggplot2)  # statistical graphics

# functions used with grid graphics to split the plotting region
# to set margins and to plot more than one ggplot object on one page/screen
vplayout <- function(x, y)
viewport(layout.pos.row=x, layout.pos.col=y)

# user-defined function to plot a ggplot object with margins
ggplot.print.with.margins <- function(ggplot.object.name,
    left.margin.pct=10,
     right.margin.pct=10,top.margin.pct=10,bottom.margin.pct=10)
    { # begin function for printing ggplot objects with margins
      # margins expressed as percentages of total... use integers
    grid.newpage()
    pushViewport(viewport(layout=grid.layout(100,100)))
    print(ggplot.object.name,
    vp=vplayout((0 + top.margin.pct):(100 - bottom.margin.pct),
        (0 + left.margin.pct):(100 - right.margin.pct)))
    } # end function for printing ggplot objects with margins

# read in payroll and performance data
# including annotation text for team abbreviations
mlb_data <- read.csv("mlb_payroll_performance_2014.csv")
mlb_data$millions <- mlb_data$payroll/1000000
mlb_data$winpercent <- mlb_data$wlpct * 100

cat("\nCorrelation between Payroll and Performance:\n")
with(mlb_data, print(cor(millions, winpercent)))

cat("\nProportion of win/loss percentage explained by payrolls:\n")
with(mlb_data, print(cor(millions, winpercent)^2))

pdf(file = "fig_understanding_markets_payroll_performance.pdf",
     width = 5.5, height = 5.5)
ggplot_object <- ggplot(data = mlb_data,
    aes(x = millions, y = winpercent)) +
    geom_point(colour = "darkblue", size = 3) +
    xlab("Team Payroll (Millions of Dollars)") +
    ylab("Percentage of Games Won") +
    geom_text(aes(label = textleft), size = 3, hjust = 1.3) +
    geom_text(aes(label = textright), size = 3, hjust = -0.25)

ggplot.print.with.margins(ggplot_object, left.margin.pct = 5,
    right.margin.pct = 5, top.margin.pct = 5, bottom.margin.pct = 5)

dev.off()

Exhibit 1.3. Making a Perceptual Map of Sports (R)

# Making a Perceptual Map of Sports (R)

library(MASS)  # includes functions for multidimensional scaling
library(wordcloud)  # textplot utility to avoid overlapping text

USE_METRIC_MDS <- FALSE  # metric versus non-metric toggle

# utility function for converting a distance structure
# to a distance matrix as required for some routines and
# for printing of the complete matrix for visual inspection.
make.distance.matrix <- function(distance_structure)
    { n <- attr(distance_structure, "Size")
      full <- matrix(0,n,n)
      full[lower.tri(full)] <- distance_structure
      full+t(full)
    }

# enter data into a distance structure as required for various
# distance-based routines. That is, we enter the upper triangle
# of the distance matrix as a single vector of distances
distance_structure <-
    as.single(c(9,11,10,5,14,4,15,6,12,13,16,1,18,2,20,7,3,19,17,8,21))

# provide a character vector of sports names
sport_names <- c("Baseball", "Basketball", "Football",
    "Soccer", "Tennis", "Hockey", "Golf")

attr(distance_structure, "Size") <- length(sport_names)  # set size attribute

# check to see that the distance structure has been entered correctly
# by converting the distance structure to a distance matrix
# using the utility function make.distance.matrix, which we had defined
distance_matrix <- unlist(make.distance.matrix(distance_structure))
cat("\n","Distance Matrix of Seven Sports","\n")
print(distance_matrix)

if (USE_METRIC_MDS)
    {
    # apply the metric multidimensional scaling algorithm and plot the map
    mds_solution <- cmdscale(distance_structure, k=2, eig=T)
    }

# apply the non-metric multidimensional scaling algorithm
# this is more appropriate for rank-order data
# and provides a more satisfactory solution here

if (!USE_METRIC_MDS)
    {
    mds_solution <- isoMDS(distance_matrix, k = 2, trace = FALSE)

    }
pdf(file = "plot_nonmetric_mds_seven_sports.pdf",
    width=8.5, height=8.5) # opens pdf plotting device
# use par(mar = c(bottom, left, top, right)) to set up margins on the plot
par(mar=c(7.5, 7.5, 7.5, 5))

# original solution
First_Dimension <- mds_solution$points[,1]
Second_Dimension <- mds_solution$points[,2]

# set up the plot but do not plot points... use names for points
plot(First_Dimension, Second_Dimension, type = "n", cex = 1.5,
    xlim = c(-15, 15), ylim = c(-15, 15))  # first page of pdf plots
# We plot the sport names in the locations where points normally go.
text(First_Dimension, Second_Dimension, labels = sport_names,
    offset = 0.0, cex = 1.5)
title("Seven Sports (initial solution)")

# reflect the horizontal dimension
# multiply the first dimension by -1 to get reflected image
First_Dimension <- mds_solution$points[,1] * -1
Second_Dimension <- mds_solution$points[,2]
plot(First_Dimension, Second_Dimension, type = "n", cex = 1.5,
    xlim = c(-15, 15), ylim = c(-15, 15))  # second page of pdf plots
text(First_Dimension, Second_Dimension, labels = sport_names,
    offset = 0.0, cex = 1.5)
title("Seven Sports (horizontal reflection)")

# reflect the vertical dimension
# multiply the section dimension by -1 to get reflected image
First_Dimension <- mds_solution$points[,1]
Second_Dimension <- mds_solution$points[,2] * -1
plot(First_Dimension, Second_Dimension, type = "n", cex = 1.5,
    xlim = c(-15, 15), ylim = c(-15, 15))  # third page of pdf plots
text(First_Dimension, Second_Dimension, labels = sport_names,
    offset = 0.0, cex = 1.5)
title("Seven Sports (vertical reflection)")

# multiply the first and second dimensions by -1
# for reflection in both horizontal and vertical directions
First_Dimension <- mds_solution$points[,1] * -1
Second_Dimension <- mds_solution$points[,2] * -1
plot(First_Dimension, Second_Dimension, type = "n", cex = 1.5,
    xlim = c(-15, 15), ylim = c(-15, 15))  # fourth page of pdf plots
text(First_Dimension, Second_Dimension, labels = sport_names,
    offset = 0.0, cex = 1.5)
title("Seven Sports (horizontal and vertical reflection)")
dev.off()  # closes the pdf plotting device

pdf(file = "plot_pretty_original_mds_seven_sports.pdf",
    width=8.5, height=8.5) # opens pdf plotting device
# use par(mar = c(bottom, left, top, right)) to set up margins on the plot
par(mar=c(7.5, 7.5, 7.5, 5))
First_Dimension <- mds_solution$points[,1]  # no reflection
Second_Dimension <- mds_solution$points[,2]   # no reflection
# wordcloud utility for plotting with no overlapping text
textplot(x = First_Dimension,
    y = Second_Dimension,
    words = sport_names,
    show.lines = FALSE,
    xlim = c(-15, 15),  # extent of horizontal axis range
    ylim = c(-15, 15),  # extent of vertical axis range
    xaxt = "n",  # suppress tick marks
    yaxt = "n",  # suppress tick marks
    cex = 1.15,  # size of text points
    mgp = c(0.85, 1, 0.85),  # position of axis labels
    cex.lab = 1.5,  # magnification of axis label text
    xlab = "",
    ylab = "")
dev.off()  # closes the pdf plotting device


pdf(file = "fig_sports_perceptual_map.pdf",
    width=8.5, height=8.5) # opens pdf plotting device
# use par(mar = c(bottom, left, top, right)) to set up margins on the plot
par(mar=c(7.5, 7.5, 7.5, 5))
First_Dimension <- mds_solution$points[,1] * -1  # reflect horizontal
Second_Dimension <- mds_solution$points[,2]
# wordcloud utility for plotting with no overlapping text
textplot(x = First_Dimension,
    y = Second_Dimension,
    words = sport_names,
    show.lines = FALSE,
    xlim = c(-15, 15),  # extent of horizontal axis range
    ylim = c(-15, 15),  # extent of vertical axis range
    xaxt = "n",  # suppress tick marks
    yaxt = "n",  # suppress tick marks
    cex = 1.15,  # size of text points
    mgp = c(0.85, 1, 0.85),  # position of axis labels
    cex.lab = 1.5,  # magnification of axis label text
    xlab = "First Dimension (Individual/Team, Degree of Contact)",
    ylab = "Second Dimension (Anaerobic/Aerobic, Other")
dev.off()  # closes the pdf plotting device