1.4. Average-Case Analysis
The mathematical techniques that we consider in this book are not just applicable to solving problems related to the performance of algorithms, but also to mathematical models for all manner of scientific applications, from genomics to statistical physics. Accordingly, we often consider structures and techniques that are broadly applicable. Still, our prime motivation is to consider mathematical tools that we need in order to be able to make precise statements about resource usage of important algorithms in practical applications.
Our focus is on average-case analysis of algorithms: we formulate a reasonable input model and analyze the expected running time of a program given an input drawn from that model. This approach is effective for two primary reasons.
The first reason that average-case analysis is important and effective in modern applications is that straightforward models of randomness are often extremely accurate. The following are just a few representative examples from sorting applications:
- Sorting is a fundamental process in cryptanalysis, where the adversary has gone to great lengths to make the data indistinguishable from random data.
- Commercial data processing systems routinely sort huge files where keys typically are account numbers or other identification numbers that are well modeled by uniformly random numbers in an appropriate range.
- Implementations of computer networks depend on sorts that again involve keys that are well modeled by random ones.
- Sorting is widely used in computational biology, where significant deviations from randomness are cause for further investigation by scientists trying to understand fundamental biological and physical processes.
As these examples indicate, simple models of randomness are effective, not just for sorting applications, but also for a wide variety of uses of fundamental algorithms in practice. Broadly speaking, when large data sets are created by humans, they typically are based on arbitrary choices that are well modeled by random ones. Random models also are often effective when working with scientific data. We might interpret Einstein’s oft-repeated admonition that “God does not play dice” in this context as meaning that random models are effective, because if we discover significant deviations from randomness, we have learned something significant about the natural world.
The second reason that average-case analysis is important and effective in modern applications is that we can often manage to inject randomness into a problem instance so that it appears to the algorithm (and to the analyst) to be random. This is an effective approach to developing efficient algorithms with predictable performance, which are known as randomized algorithms. M. O. Rabin [25] was among the first to articulate this approach, and it has been developed by many other researchers in the years since. The book by Motwani and Raghavan [23] is a thorough introduction to the topic.
Thus, we begin by analyzing random models, and we typically start with the challenge of computing the mean—the average value of some quantity of interest for N instances drawn at random. Now, elementary probability theory gives a number of different (though closely related) ways to compute the average value of a quantity. In this book, it will be convenient for us to explicitly identify two different approaches to doing so.
Distributional
Let ΠN be the number of possible inputs of size N and ΠNk be the number of inputs of size N that cause the algorithm to have cost k, so that ΠN = ∑k ΠNk. Then the probability that the cost is k is ΠNk/ΠN and the expected cost is
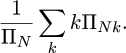
The analysis depends on “counting.” How many inputs are there of size N and how many inputs of size N cause the algorithm to have cost k? These are the steps to compute the probability that the cost is k, so this approach is perhaps the most direct from elementary probability theory.
Cumulative
Let ΣN be the total (or cumulated) cost of the algorithm on all inputs of size N. (That is, ΣN = ∑kkΠNk, but the point is that it is not necessary to compute ΣN in that way.) Then the average cost is simply ΣN/ΠN. The analysis depends on a less specific counting problem: what is the total cost of the algorithm, on all inputs? We will be using general tools that make this approach very attractive.
The distributional approach gives complete information, which can be used directly to compute the standard deviation and other moments. Indirect (often simpler) methods are also available for computing moments when using the cumulative approach, as we will see. In this book, we consider both approaches, though our tendency will be toward the cumulative method, which ultimately allows us to consider the analysis of algorithms in terms of combinatorial properties of basic data structures.
Many algorithms solve a problem by recursively solving smaller subproblems and are thus amenable to the derivation of a recurrence relationship that the average cost or the total cost must satisfy. A direct derivation of a recurrence from the algorithm is often a natural way to proceed, as shown in the example in the next section.
No matter how they are derived, we are interested in average-case results because, in the large number of situations where random input is a reasonable model, an accurate analysis can help us:
- Compare different algorithms for the same task.
- Predict time and space requirements for specific applications.
- Compare different computers that are to run the same algorithm.
- Adjust algorithm parameters to optimize performance.
The average-case results can be compared with empirical data to validate the implementation, the model, and the analysis. The end goal is to gain enough confidence in these that they can be used to predict how the algorithm will perform under whatever circumstances present themselves in particular applications. If we wish to evaluate the possible impact of a new machine architecture on the performance of an important algorithm, we can do so through analysis, perhaps before the new architecture comes into existence. The success of this approach has been validated over the past several decades: the sorting algorithms that we consider in the section were first analyzed more than 50 years ago, and those analytic results are still useful in helping us evaluate their performance on today’s computers.

