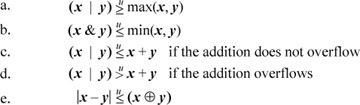- 2-1 Manipulating Rightmost Bits
- 2-2 Addition Combined with Logical Operations
- 2-3 Inequalities among Logical and Arithmetic Expressions
- 2-4 Absolute Value Function
- 2-5 Average of Two Integers
- 2-6 Sign Extension
- 2-7 Shift Right Signed from Unsigned
- 2-8 Sign Function
- 2-9 Three-Valued Compare Function
- 2-10 Transfer of Sign Function
- 2-11 Decoding a "Zero Means 2 **n" Field
- 2-12 Comparison Predicates
- 2-13 Overflow Detection
- 2-14 Condition Code Result of Add, Subtract, and Multiply
- 2-15 Rotate Shifts
- 2-16 Double-Length Add/Subtract
- 2-17 Double-Length Shifts
- 2-18 Multibyte Add, Subtract, Absolute Value
- 2-19 Doz, Max, Min
- 2-20 Exchanging Registers
- 2-21 Alternating among Two or More Values
- 2-22 A Boolean Decomposition Formula
- 2-23 Implementing Instructions for All 16 Binary Boolean Operations
This chapter is from the book
This chapter is from the book
This chapter is from the book
2–3 Inequalities among Logical and Arithmetic Expressions
Inequalities among binary logical expressions whose values are interpreted as unsigned integers are nearly trivial to derive. Here are two examples:
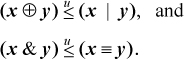
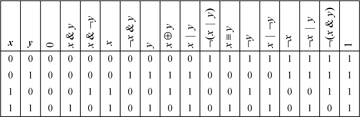
These can be derived from a list of all binary logical operations, shown in Table 2–1.
Table 2-1. The 16 Binary Logical Operations
)
Let f(x, y) and g(x, y) represent two columns in Table 2–1. If for each row in which f(x,y) is 1, g(x,y) also is 1, then for all (x,y), f(x, y)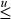 
g(x, y). Clearly, this extends to word-parallel logical operations. One can easily read off such relations (most of which are trivial) as (x & y) 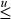x 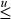(x | ¬ y), and so on. Furthermore, if two columns have a row in which one entry is 0 and the other is 1, and another row in which the entries are 1 and 0, respectively, then no inequality relation exists between the corresponding logical expressions. So the question of whether or not f(x, y) 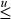g(x, y) is completely and easily solved for all binary logical functions f and g.
Use caution when manipulating these relations. For example, for ordinary arithmetic, if x + y ≤ a and z ≤ x, then z + y ≤ a, but this inference is not valid if “+” is replaced with or.
Inequalities involving mixed logical and arithmetic expressions are more interesting. Below is a small selection.
)
The proofs of these are quite simple, except possibly for the relation |x − y| 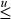(x ⊕ y). By |x − y| we mean the absolute value of x − y, which can be computed within the domain of unsigned numbers as max(x, y) − min(x, y). This relation can be proven by induction on the length of x and y (the proof is a little easier if you extend them on the left rather than on the right).