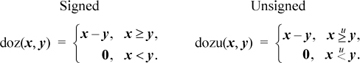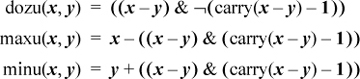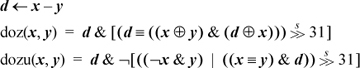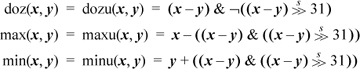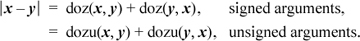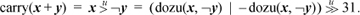- 2-1 Manipulating Rightmost Bits
- 2-2 Addition Combined with Logical Operations
- 2-3 Inequalities among Logical and Arithmetic Expressions
- 2-4 Absolute Value Function
- 2-5 Average of Two Integers
- 2-6 Sign Extension
- 2-7 Shift Right Signed from Unsigned
- 2-8 Sign Function
- 2-9 Three-Valued Compare Function
- 2-10 Transfer of Sign Function
- 2-11 Decoding a "Zero Means 2 **n" Field
- 2-12 Comparison Predicates
- 2-13 Overflow Detection
- 2-14 Condition Code Result of Add, Subtract, and Multiply
- 2-15 Rotate Shifts
- 2-16 Double-Length Add/Subtract
- 2-17 Double-Length Shifts
- 2-18 Multibyte Add, Subtract, Absolute Value
- 2-19 Doz, Max, Min
- 2-20 Exchanging Registers
- 2-21 Alternating among Two or More Values
- 2-22 A Boolean Decomposition Formula
- 2-23 Implementing Instructions for All 16 Binary Boolean Operations
This chapter is from the book
This chapter is from the book
This chapter is from the book
2–19 Doz, Max, Min
The “doz” function is “difference or zero,” defined as follows:
)
It has been called “first grade subtraction” because the result is 0 if you try to take away too much.3 If implemented as a computer instruction, perhaps its most important use is to implement the max(x, y) and min(x, y) functions (in both signed and unsigned forms) in just two simple instructions, as will be seen. Implementing max(x, y) and min(x, y) in hardware is difficult because the machine would need paths from the output ports of the register file back to an input port, bypassing the adder. These paths are not normally present. If supplied, they would be in a region that’s often crowded with wiring for register bypasses. The situation is illustrated in Figure 2.3. The adder is used (by the instruction) to do the subtraction x − y. The high-order bits of the result of the subtraction (sign bit and carries, as described on page 27) define whether x ≥ y or x < y The comparison result is fed to a multiplexor (MUX) that selects either x or y as the result to write into the target register. These paths, from register file outputs x and y to the multiplexor, are not normally present and would have little use. The difference or zero instructions can be implemented without these paths because it is the output of the adder (or 0) that is fed back to the register file.
)
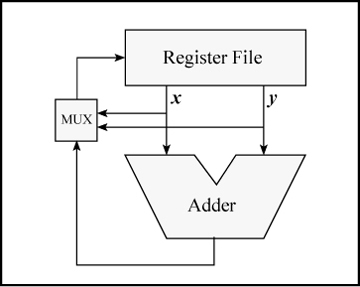
Figure 2-3. Implementing max(x, y) and min(x, y).
Using difference or zero, max(x, y) and min(x, y) can be implemented in two instructions as follows:
)
In the signed case, the result of the difference or zero instruction can be negative. This happens if overflow occurs in the subtraction. Overflow should be ignored; the addition of y or subtraction from x will overflow again, and the result will be correct. When doz(x, y) is negative, it is actually the correct difference if it is interpreted as an unsigned integer.
Suppose your computer does not have the difference or zero instructions, but you want to code doz(x, y), max(x, y), and so forth, in an efficient branch-free way. In the next few paragraphs we show how these functions might be coded if your machine has the conditional move instructions, comparison predicates, efficient access to the carry bit, or none of these.
If your machine has the conditional move instructions, it can get doz(x, y) in three instructions, and destructive 4 max(x, y) and min(x, y) in two instructions. For example, on the full RISC, z ← doz(x, y) can be calculated as follows (r0 is a permanent zero register):
sub z,x,y Set z = x - y. cmplt t,x,y Set t = 1 if x < y, else 0. movne z,t,r0 Set z = 0 if x < y.
Also on the full RISC, x ← max(x, y) can be calculated as follows:
cmplt t,x,y Set t = 1 if x < y, else 0. movne x,t,y Set x = y if x < y.
The min function, and the unsigned counterparts, are obtained by changing the comparison conditions.
These functions can be computed in four or five instructions using comparison predicates (three or four if the comparison predicates give a result of –1 for “true”):
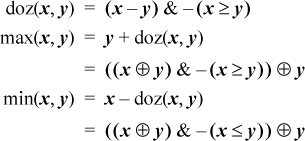
On some machines, the carry bit may be a useful aid to computing the unsigned versions of these functions. Let carry(x − y) denote the bit that comes out of the adder for the operation x+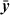 
+ 1, moved to a GPR. Thus, carry(x − y) = 1 iff x ≥ y. Then we have
)
On most machines that have a subtract that generates a carry or borrow, and another form of subtract that uses that carry or borrow as an input, the expression carry (x − y) − 1 can be computed in one more instruction after the subtraction of y from x. For example, on the Intel x86 machines, minu(x, y) can be computed in four instructions as follows:
sub eax,ecx ; Inputs x and y are in eax and ecx resp. sbb edx,edx ; edx = 0 if x >= y, else -1. and eax,edx ; 0 if x >= y, else x - y. add eax,ecx ; Add y, giving y if x >= y, else x.
In this way, all three of the functions can be computed in four instructions (three instructions for dozu(x, y) if the machine has and with complement).
A method that applies to nearly any RISC is to use one of the above expressions that employ a comparison predicate, and to substitute for the predicate one of the expressions given on page 23. For example:
)
These require from seven to ten instructions, depending on the computer’s instruction set, plus one more to get max or min.
These operations can be done in four branch-free basic RISC instructions if it is known that −231 ≤ x − y ≤ 231 − 1 (that is an expression in ordinary arithmetic, not computer arithmetic). The same code works for both signed and unsigned integers, with the same restriction on x and y. A sufficient condition for these formulas to be valid is that, for signed integers, −230 ≤ x, y ≤ 230 − 1, and for unsigned integers, 0 ≤ x,y≤231 −1.
)
Some uses of the difference or zero instruction are given here. In these, the result of doz(x, y) must be interpreted as an unsigned integer.
- It directly implements the Fortran IDIM function.
- To compute the absolute value of a difference [Knu7]:
Corollary: |x| = doz(x, 0) + doz(0, x) (other three-instruction solutions are given on page 18).
- To clamp the upper limit of the true sum of unsigned integers x and y to the maximum positive number (232 − 1) [Knu7]:
¬dozu(¬x, y).
Some comparison predicates (four instructions each):
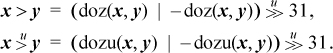
- The carry bit from the addition x + y (five instructions):
)
)
The expression doz(x, − y), with the result interpreted as an unsigned integer, is in most cases the true sum x + y with the lower limit clamped at 0. However, it fails if y is the maximum negative number.
The IBM RS/6000 computer, and its predecessor the 801, have the signed version of difference or zero. Knuth’s MMIX computer [Knu7] has the unsigned version (including some varieties that operate on parts of words in parallel). This raises the question of how to get the signed version from the unsigned version, and vice versa. This can be done as follows (where the additions and subtractions simply complement the sign bit):
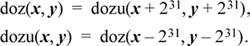
Some other identities that may be useful are:
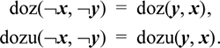
The relation doz(−x, −y) = doz(y, x) fails if either x or y, but not both, is the maximum negative number.