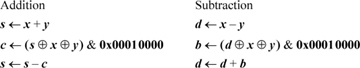- 2-1 Manipulating Rightmost Bits
- 2-2 Addition Combined with Logical Operations
- 2-3 Inequalities among Logical and Arithmetic Expressions
- 2-4 Absolute Value Function
- 2-5 Average of Two Integers
- 2-6 Sign Extension
- 2-7 Shift Right Signed from Unsigned
- 2-8 Sign Function
- 2-9 Three-Valued Compare Function
- 2-10 Transfer of Sign Function
- 2-11 Decoding a "Zero Means 2 **n" Field
- 2-12 Comparison Predicates
- 2-13 Overflow Detection
- 2-14 Condition Code Result of Add, Subtract, and Multiply
- 2-15 Rotate Shifts
- 2-16 Double-Length Add/Subtract
- 2-17 Double-Length Shifts
- 2-18 Multibyte Add, Subtract, Absolute Value
- 2-19 Doz, Max, Min
- 2-20 Exchanging Registers
- 2-21 Alternating among Two or More Values
- 2-22 A Boolean Decomposition Formula
- 2-23 Implementing Instructions for All 16 Binary Boolean Operations
This chapter is from the book
This chapter is from the book
This chapter is from the book
2–18 Multibyte Add, Subtract, Absolute Value
Some applications deal with arrays of short integers (usually bytes or halfwords), and often execution is faster if they are operated on a word at a time. For definiteness, the examples here deal with the case of four 1-byte integers packed into a word, but the techniques are easily adapted to other packings, such as a word containing a 12-bit integer and two 10-bit integers, and so on. These techniques are of greater value on 64-bit machines, because more work is done in parallel.
Addition must be done in a way that blocks the carries from one byte into another. This can be accomplished by the following two-step method:
- 1. Mask out the high-order bit of each byte of each operand and add (there will then be no carries across byte boundaries).
- 2. Fix up the high-order bit of each byte with a 1-bit add of the two operands and the carry into that bit.
The carry into the high-order bit of each byte is given by the high-order bit of each byte of the sum computed in step 1. The subsequent similar method works for subtraction:
)
These execute in eight instructions, counting the load of 0x7F7F7F7F, on a machine that has a full set of logical instructions. (Change the and and or of 0x80808080 to and not and or not, respectively, of 0x7F7F7F7F.)
There is a different technique for the case in which the word is divided into only two fields. In this case, addition can be done by means of a 32-bit addition followed by subtracting out the unwanted carry. On page 30 we noted that the expression (x + y) ⊕ x ⊕ y gives the carries into each position. Using this and similar observations about subtraction gives the following code for adding/subtracting two halfwords modulo 216 (seven instructions):
)
Multibyte absolute value is easily done by complementing and adding 1 to each byte that contains a negative integer (that is, has its high-order bit on). The following code sets each byte of y equal to the absolute value of each byte of x (eight instructions):
)
The third line could as well be m ← a + a − b. The addition of b in the fourth line cannot carry across byte boundaries, because the quantity x ⊕ m has a high-order 0 in each byte.