This chapter is from the book
This chapter is from the book
This chapter is from the book
1.6. Standard Continuous Distributions
This section presents some standard continuous distributions. Recall from Sections 1.3 that, unlike discrete random variables, the domain of a continuous random variable is a subset of the real line.
1.6.1. Uniform Distribution
A random variable X is said to be uniformly randomly distributed in the domain [a,b] if its density function f(x) = 1/(b – a) when x lies in [a,b] and is 0 otherwise. The expected value of a uniform random variable with parameters a,b is (a + b)/2.
1.6.2. Gaussian, or Normal, Distribution
A random variable is Gaussian, or normally distributed, with parameters μ and σ2 if its density is given by
We denote a Gaussian random variable X with parameters μ and σ2 as X ~ N(μ,σ2), where we read the “~” as “is distributed as.”
The Gaussian distribution can be obtained as the limiting case of the binomial distribution as n tends to infinity and p is kept constant. That is, if we have a very large number of independent trials, such that the random variable measures the number of trials that succeed, the random variable is Gaussian. Thus, Gaussian random variables naturally occur when we want to study the statistical properties of aggregates.
The Gaussian distribution is called normal because many quantities, such as the heights of people, the slight variations in the size of a manufactured item, and the time taken to complete an activity approximately follow the well-known bell-shaped curve.4
When performing experiments or simulations, it is often the case that the same quantity assumes different values during different trials. For instance, if five students were each measuring the pH of a reagent, it is likely that they would get five slightly different values. In such situations, it is common to assume that these quantities, which are supposed to be the same, are in fact normally distributed about some mean. Generally speaking, if you know that a quantity is supposed to have a certain standard value but you also know that there can be small variations in this value due to many small and independent random effects, it is reasonable to assume that the quantity is a Gaussian random variable with its mean centered on the expected value.
The expected value of a Gaussian random variable with parameters μ and σ2 is μ and its variance is σ2. In practice, it is often convenient to work with a standard Gaussian distribution, which has a zero mean and a variance of 1. It is possible to convert a Gaussian random variable X with parameters μ and σ2 to a Gaussian random variable Y with parameters 0,1 by choosing Y = (X – μ)/σ.
The Gaussian distribution is symmetric about the mean and asymptotes to 0 at +∞ and –∞. The σ2 parameter controls the width of the central “bell”: The larger this parameter, the wider the bell, and the lower the maximum value of the density function as shown in Figure 1.4. The probability that a Gaussian random variable X lies between μ – σ and μ+ σ is approximately 68.26%; between μ – 2σ and μ+ 2σ is approximately 95.44%; and between μ – 3σ and μ + 3σ is approximately 99.73%.
){kind=link}
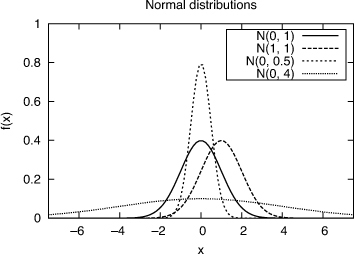
Figure 1.4. Gaussian distributions for different values of the mean and variance
It is often convenient to use a Gaussian continuous random variable to approximately model a discrete random variable. For example, the number of packets arriving on a link to a router in a given fixed time interval will follow a discrete distribution. Nevertheless, by modeling it using a continuous Gaussian random variable, we can get quick estimates of its expected extremal values.
The MGF of the normal distribution is given by
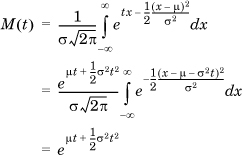
where in the last step, we recognize that the integral is the area under a normal curve, which evaluates to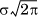 
. Note that the MGF of a normal variable with zero mean and a variance of 1 is therefore
We can use the MGF of a normal distribution to prove some elementary facts about it.
If X ~ N(μ,σ2), then a+bX ~(a + bμ, b2σ2), because the MGF of a + bX is
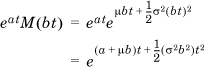
which can be seen to be a normally distributed random variable with mean a + bμ and variance b2σ2.
- If X ~ N(μ,σ2), then Z = (X – μ)/σ ~ N(0,1). This is obtained trivially by substituting for a and b in expression (a). Z is called the standard normal variable.
- If X ~N(μ1,σ12) and X and Y are independent,
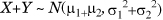, because the MGF of their sum is the product of their individual 
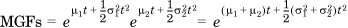. As a generalization, the sum of any number of independent normal variables is also normally distributed with the mean as the sum of the individual means and the variance as the sum of the individual variances.
1.6.3. Exponential Distribution
A random variable X is exponentially distributed with parameter λ, where λ >0, if its density function is given by
Note than when x = 0, f(x) = λ (see Figure 1.5). The expected value of such a random variable is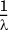 
and its variance is 
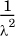. The exponential distribution is the continuous analog of the geometric distribution. Recall that the geometric distribution measures the number of trials until the first success. Correspondingly, the exponential distribution arises when we are trying to measure the duration of time before some event happens (i.e., achieves success). For instance, it is used to model the time between two consecutive packet arrivals on a link.
)
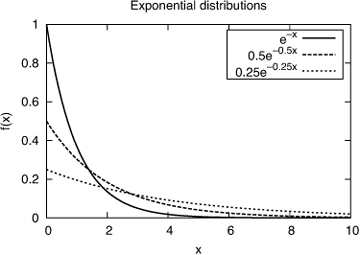
Figure 1.5 Exponentially distributed random variables with λ = {1, 0.5, 0.25}
The cumulative density function of the exponential distribution, F(X), is given by
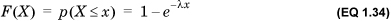
An important property of the exponential distribution is that, like the geometric distribution, it is memoryless and, in fact, is the only memoryless continuous distribution. Intuitively, this means that the expected remaining time until the occurrence of an event with an exponentially distributed waiting time is independent of the time at which the observation is made. More precisely, P(X > s+t | X>s) = P(X>t) for all s, t. From a geometric perspective, if we truncate the distribution to the left of any point on the positive X axis and then rescale the remaining distribution so that the area under the curve is 1, we will obtain the original distribution. The following examples illustrate this useful property.
1.6.4. Power-Law Distribution
A random variable described by its minimum value xmin and a scale parameter α > 1 is said to obey the power-law distribution if its density function is given by
Typically, this function needs to be normalized for a given set of parameters to ensure that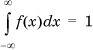 
.
Note that f(x) decreases rapidly with x. However, the decline is not as rapid as with an exponential distribution (see Figure 1.6). This is why a power-law distribution is also called a heavy-tailed distribution. When plotted on a log-log scale, the graph of f(x) versus x shows a linear relationship with a slope of –α, which is often used to quickly identify a potential power-law distribution in a data set.
)
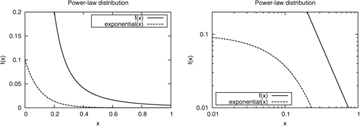
Figure 1.6. A typical power-law distribution with parameters xmin = 0.1 and α = 2.3 compared to an exponential distribution using a linear-linear (left) and a log-log (right) scale
Intuitively, if we have objects distributed according to an exponential or power law, a few “elephants” occur frequently and are common, and many “mice” are relatively uncommon. The elephants are responsible for most of the probability mass. From an engineering perspective, whenever we see such a distribution, it makes sense to build a system that deals well with the elephants, even at the expense of ignoring the mice. Two rules of thumb that reflect this are the 90/10 rule—90% of the output is derived from 10% of the input—and the dictum optimize for the common case.
When α < 2, the expected value of the random variable is infinite. A system described by such a random variable is unstable (i.e., its value is unbounded). On the other hand, when α > 2, the tail probabilities fall rapidly enough that a powerlaw random variable can usually be well approximated by an exponential random variable.
A widely studied example of power-law distribution is the random variable that describes the number of users who visit one of a collection of Web sites on the Internet on any given day. Traces of Web site accesses almost always show that all but a microscopic fraction of Web sites get fewer than one visitor a day: Traffic is garnered mostly by a handful of well-known Web sites.