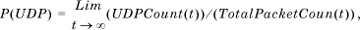Mathematical Foundations of Computer Networking: Probability
1.1. Introduction
The concept of probability pervades every aspect of our lives. Weather forecasts are couched in probabilistic terms, as are economic predictions and even outcomes of our own personal decisions. Designers and operators of computer networks need to often think probabilistically, for instance, when anticipating future traffic workloads or computing cache hit rates. From a mathematical standpoint, a good grasp of probability is a necessary foundation to understanding statistics, game theory, and information theory. For these reasons, the first step in our excursion into the mathematical foundations of computer networking is to study the concepts and theorems of probability.
This chapter is a self-contained introduction to the theory of probability. We begin by introducing the elementary concepts of outcomes, events, and sample spaces, which allows us to precisely define the conjunctions and disjunctions of events. We then discuss concepts of conditional probability and Bayes’s rule. This is followed by a description of discrete and continuous random variables, expectations and other moments of a random variable, and the moment generating function. We discuss some standard discrete and continuous distributions and conclude with some useful theorems of probability and a description of Bayesian networks.
Note that in this chapter, as in the rest of the book, the solved examples are an essential part of the text. They provide a concrete grounding for otherwise abstract concepts and are necessary to understand the material that follows.
1.1.1. Outcomes
The mathematical theory of probability uses terms such as outcome and event with meanings that differ from those in common practice. Therefore, we first introduce a standard set of terms to precisely discuss probabilistic processes. These terms are shown in boldface. We will use the same convention to introduce other mathematical terms in the rest of the book.
Probability measures the degree of uncertainty about the potential outcomes of a process. Given a set of distinct and mutually exclusive outcomes of a process, denoted {o1,o2, ...}, called the sample space S, the probability of any outcome, denoted P(oi), is a real number between 0 and 1, where 1 means that the outcome will surely occur, 0 means that it surely will not occur, and intermediate values reflect the degree to which one is confident that the outcome will or will not occur.1 We assume that it is certain that some element in S occurs. Hence, the elements of S describe all possible outcomes, and the sum of probability of all the elements of S is always 1.
1.1.2. Events
The definition of probability naturally extends to any subset of elements of S, which we call an event, denoted E. If the sample space is discrete, every event E is an element of the power set of S, which is the set of all possible subsets of S. The probability associated with an event, denoted P(E), is a real number 0 ≤P(E) ≤ 1 and is the sum of the probabilities associated with the outcomes in the event.
1.1.3. Disjunctions and Conjunctions of Events
Consider an event E that is considered to have occurred if either or both of two other events E1 or E2 occur, where both events are defined in the same sample space. Then, E is said to be the disjunction, or logical OR, of the two events denoted E = E1 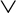 E2 and read “E1 or E2.”
E2 and read “E1 or E2.”
In contrast, consider event E that is considered to have occurred only if both of two other events E1 or E2 occur, where both are in the same sample space. Then, E is said to be the conjunction, or logical AND, of the two events denoted E = E1 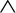 E2 and read “ E1 and E2.” When the context is clear, we abbreviate this to E = E1 E2.
E2 and read “ E1 and E2.” When the context is clear, we abbreviate this to E = E1 E2.
Two events Ei and Ej in S are mutually exclusive if only one of the two may occur simultaneously. Because the events have no outcomes in common, P(Ei 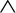 Ej) = P ({ }) = 0. Note that outcomes are always mutually exclusive, but events need not be so.
Ej) = P ({ }) = 0. Note that outcomes are always mutually exclusive, but events need not be so.
1.1.4. Axioms of Probability
One of the breakthroughs in modern mathematics was the realization that the theory of probability can be derived from just a handful of intuitively obvious axioms. Several variants of the axioms of probability are known. We present the three axioms as stated by Kolmogorov to emphasize the simplicity and elegance that lie at the heart of probability theory.
- 0≤P(E)≤1; that is, the probability of an event lies between 0 and 1.
- P(S) = 1, that is, it is certain that at least some event in S will occur.
- Given a potentially infinite set of mutually exclusive events E1,E2,...

That is, the probability that any one of the events in the set of mutually exclusive events occurs is the sum of their individual probabilities. For any finite set of n mutually exclusive events, we can state the axiom equivalently as

An alternative form of axiom 3 is:
This alternative form applies to non–mutually exclusive events.
1.1.5. Subjective and Objective Probability
The axiomatic approach is indifferent as to how the probability of an event is determined. It turns out that there are two distinct ways in which to determine the probability of an event. In some cases, the probability of an event can be derived from counting arguments. For instance, given the roll of a fair die, we know that only six outcomes are possible and that all outcomes are equally likely, so that the probability of rolling, say, a 1, is 1/6. This is called its objective probability. Another way of computing objective probabilities is to define the probability of an event as being the limit of a counting process, as the next example shows.
In contrast to an objective assessment of probability, we can also use probabilities to characterize events subjectively.
The subjective and frequentist approaches interpret zero-probability events differently. Consider an infinite sequence of successive events. Any event that occurs only a finite number of times in this infinite sequence will have a frequency that can be made arbitrarily small. In number theory, we do not and cannot differentiate between a number that can be made arbitrarily small and zero. So, from this perspective, such an event can be considered to have a probability of occurrence of zero even though it may occur a finite number of times in the sequence.
From a subjective perspective, a zero-probability event is defined as an event E such that a rational person would be willing to bet an arbitrarily large but finite amount that E will not occur. More concretely, suppose that this person were to receive a reward of $1 if E did not occur but would have to forfeit a sum of $F if E occurred. Then, the bet would be taken for any finite value of F.
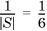 .
.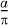 ., which tends to zero as a tends to zero.
., which tends to zero as a tends to zero.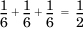 . We write P({1,3,5}) = 0.5.
. We write P({1,3,5}) = 0.5.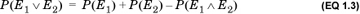
 .
. .
.