1.3. Random Variables
So far, we have restricted ourselves to studying events, which are collections of outcomes of experiments or observations. However, we are often interested in abstract quantities or outcomes of experiments that are derived from events and observations but are not themselves events or observations. For example, if we throw a fair die, we may want to compute the probability that the square of the face value is smaller than 10. This is random and can be associated with a probability and, moreover, depends on some underlying random events. Yet, it is neither an event nor an observation: It is a random variable. Intuitively, a random variable is a quantity that can assume any one of a set of values, called its domain D, and whose value can be stated only probabilistically. In this section, we will study random variables and their distributions.
More formally, a real random variable—the one most commonly encountered in applications having to do with computer networking—is a mapping from events in a sample space S to the domain of real numbers. The probability associated with each value assumed by a real random variable2 is the probability of the underlying event in the sample space, as illustrated in Figure 1.1.
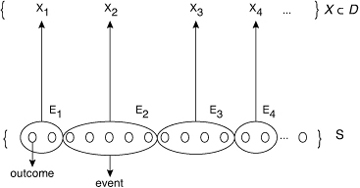
Figure 1.1. The random variable X takes on values from the domain D. Each value taken on by the random variable is associated with a probability corresponding to an event E, which is a subset of outcomes in the sample space S.
A random variable is discrete if the set of values it can assume is finite and countable. The elements of D should be mutually exclusive—that is, the random variable cannot simultaneously take on more than one value—and exhaustive—the random variable cannot assume a value that is not an element of D.
A random variable is continuous if the values it can take on are a subset of the real line.
1.3.1. Distribution
In many cases, we are not interested in the actual value taken by a random variable but in the probabilities associated with each such value that it can assume. To make this more precise, consider a discrete random variable Xd that assumes distinct values D = {x1, x2,..., xn}. We define the value p(xi) to be the probability of the event that results in Xd assuming the value xi. The function p(Xd), which characterizes the probability that Xd will take on each value in its domain, is called the probability mass function of Xd.3 It is also sometimes called the distribution of Xd.
Unlike a discrete random variable, which has nonzero probability of taking on any particular value in its domain, the probability that a continuous real random variable Xc will take on any specific value in its domain is 0. Nevertheless, in nearly all cases of interest in the field of computer networking, we will be able to assume that we can define the density function f(x) of Xc as follows: The probability that Xc takes on a value between two reals, x1 and x2, p(x1 ≤ x ≤ x2), is given by the integral 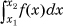 . Of course, we need to ensure that
. Of course, we need to ensure that 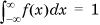 . Alternatively, we can think of f(x) being implicitly defined by the statement that a variable x chosen randomly in the domain of Xc has probability f(α)Δ of lying in the range
. Alternatively, we can think of f(x) being implicitly defined by the statement that a variable x chosen randomly in the domain of Xc has probability f(α)Δ of lying in the range 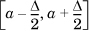 when Δ is very small.
when Δ is very small.
1.3.2. Cumulative Density Function
The domain of a discrete real random variable Xd is totally ordered; that is, for any two values x1 and x2 in the domain, either x1 > x2 or x2 > x1. We define the cumulative density function F(Xd) by
Note the difference between F(Xd), which denotes the cumulative distribution of random variable Xd, and F(x), which is the value of the cumulative distribution for the value Xd = x.
Similarly, the cumulative density function of a continuous random variable Xc, denoted F(Xc), is given by
By definition of probability, in both cases,0 ≤ F(Xd)≤ 1, 0 ≤ F(Xc)≤1.
1.3.3. Generating Values from an Arbitrary Distribution
The cumulative density function F(X), where X is either discrete or continuous, can be used to generate values drawn from the underlying discrete or continuous distribution p(Xd) or f(Xc), as illustrated in Figure 1.2. Consider a discrete random variable Xd that takes on values x1,x2,...xn with probabilities p(xi). By definition, F(xk) = F(xk – 1) + p(xk). Moreover, F(Xd) always lies in the range [0,1]. Therefore, if we were to generate a random number u with uniform probability in the range [0,1], the probability that u lies in the range [F(xk – 1),F(xk)] is p(xk). Moreover, xk = F–1(u). Therefore, the procedure to generate values from the discrete distribution p(Xd) is as follows: First, generate a random variable u uniformly in the range [0,1]; second, compute xk = F –1(u).
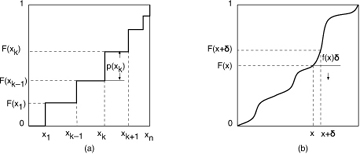
Figure 1.2. Generating values from an arbitrary (a) discrete or (b) continuous distribution
We can use a similar approach to generate values from a continuous random variable Xc with associated density function f(Xc). By definition, F(x + δ) = F(x) + f(x)δ for very small values of δ. Moreover, F(Xc) always lies in the range [0,1]. Therefore, if we were to generate a random number u with uniform probability in the range [0,1], the probability that u lies in the range [F(x),F(x + δ)] is f(x)δ, which means that x = F–1(u) is distributed according to the desired density function f(Xc). Therefore, the procedure to generate values from the continuous distribution f(Xc) is as follows: First, generate a random variable u uniformly in the range [0,1]; second, compute x = F–1(u).
1.3.4. Expectation of a Random Variable
The expectation, mean, or expected value E[Xd] of a discrete random variable Xd that can take on n values xi with probability p(xi) is given by

Similarly, the expectation E[Xc] of a continuous random variable Xc with density function f(x) is given by

Intuitively, the expected value of a random variable is the value we expect it to take, knowing nothing else about it. For instance, if you knew the distribution of the random variable corresponding to the time it takes for you to travel from your home to work, you expect your commute time on a typical day to be the expected value of this random variable.
The expectation of a random variable gives us a reasonable idea of how it behaves in the long run. It is important to remember, however, that two random variables with the same expectation can have rather different behaviors.
We now state, without proof, four useful properties of expectations.
- For constants a and b:

- E[X + Y] = E[X] + E[Y], or, more generally, for any set of random variables Xi:

- For a discrete random variable Xd with probability mass function p(xi) and any function g(.):

- For a continuous random variable Xc with density function f(x) and any function g(.):

Note that, in general, E[g(X)] is not the same as g(E[X]); that is, a function cannot be taken out of the expectation.
1.3.5. Variance of a Random Variable
The variance of a random variable is defined by V(X) = E[(X – E[X])2]. Intuitively, it shows how far away the values taken on by a random variable would be from its expected value. We can express the variance of a random variable in terms of two expectations as V(X) = E[X2] – E[X]2. For
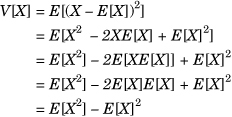
In practical terms, the distribution of a random variable over its domain D—this domain is also called the population—is not usually known. Instead, the best we can do is to sample the values it takes on by observing its behavior over some period of time. We can estimate the variance of the random variable by keeping running counters for 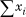 and
and 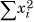 . Then,
. Then,
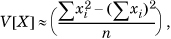
where this approximation improves with n, the size of the sample, as a consequence of the law of large numbers, discussed in Section 1.7.4.
The following properties of the variance of a random variable can be easily shown for both discrete and continuous random variables.
- For constant a:

- For constant a:

- If X and Y are independent random variables:

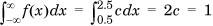 . The probability that the interarrival time is in the interval
. The probability that the interarrival time is in the interval 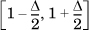 is therefore 0.5Δ.
is therefore 0.5Δ.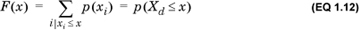
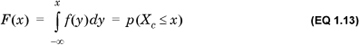
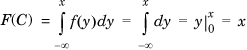 . We see that, although, for example, f(0.1) = 1, this does not mean that the value 0.1 is certain!
. We see that, although, for example, f(0.1) = 1, this does not mean that the value 0.1 is certain!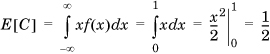
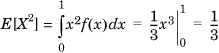 .
.