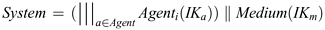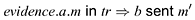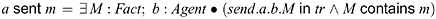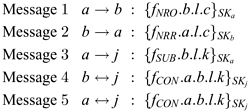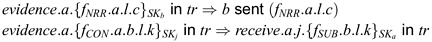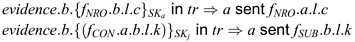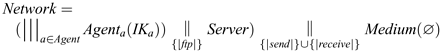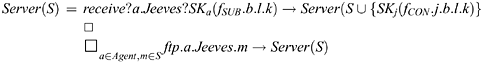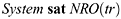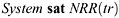- The Yahalom protocol
- Secrecy
- Authentication
- Non-repudiation
- Anonymity
- Summary
This chapter is from the book
This chapter is from the book
This chapter is from the book
3.4 Non-repudiation
Non-repudiation protocols are used to enable agents to send and receive messages, and provide them each with evidence so that neither of them can successfully deny at a later time that the message was transmitted or received. Participants aim to collect evidence to prove that the other party did send or receive the message (as appropriate). Non-repudiation evidence can be generated for one party or for both parties. A protocol designed to achieve this is generally required to provide the property of correctness of the evidence: that the evidence really is strong enough to guarantee what the holder requires of it. Evidence is often in the form of signed messages, which provide guarantees concerning their originator.
In some cases where evidence is provided to both parties, the protocol might also aim to provide fairness: that no party should be able to reach a point where they have the evidence or the message that they require without the other party also having their required evidence. Fairness is not required for non-repudiation, but it may be desirable in some cases from the point of view of the participants.
In contrast to authentication and key-exchange protocols, non-repudiation protocols are not concerned with communication in the presence of an intruder between two parties who trust each other. Instead they are used when a communication is required between two agents who require protection from each other and who do not entirely trust each other to behave honourably in the future. They are typically proposed in the context of a passive communication medium that cannot be manipulated by either party or by other agents, but which may nevertheless have some unreliable behaviour.
In analysis, the system must be modelled from the point of view of the environment of the system that would be used to arbitrate in the case of a dispute. Correctness is concerned with whether the environment, which cannot know a priori which agents are honest, must accept evidence as guaranteeing that the message was sent. This concerns the nature of evidence: an agent might himself know that a message was sent, and yet not be in a position to prove this to anyone else.
This means that for the modelling and analysis of non-repudiation protocols, a different threat model must be used. In deciding whether a particular message has been sent, neither of the participants can be trusted to behave according to the protocol, and the possibility that either or both of them do not behave honestly must be allowed. However, it will generally have to be assumed that trusted third parties (which are sometimes used in non-repudiation protocols) do behave according to the protocol.
Although the threat model is different, non-repudiation properties are expressed in a similar way to authentication: that the occurrence of some event guarantees that some previous message was sent. The provision of a certain piece of evidence should guarantee that a particular message was previously sent by a particular party.
A non-repudiation protocol is thus concerned with the creation of evidence for the parties involved. Correctness will be concerned with the suitability of the evidence, and the analysis (given the altered threat model) will have to take into account the fact that the participants might not behave in accordance with the protocol. These parties are therefore modelled almost as the intruder is for secrecy and authentication analysis: that they can behave in any way in line with their capabilities, apart from some elementary security requirements, for example that they do not give away their private keys. Their capabilities with these assumptions built in will be encapsulated into a relation ⊢a, which is essentially the same as ⊢ except that a’s private keys cannot appear as part of any fact on the right-hand side: we assume that the agent will never give out his own private key in any form.
The behaviour of an arbitrary user of the network is therefore described by the CSP process description Agenta:
)
An agent with information S is able to send any data in S, and can also present any such information as evidence. He can also receive any message m (which will increase S) from the medium.
Depending on the context of the protocol, the medium might be considered to be under the control of an intruder, or it may be considered simply to be an unreliable medium. Which of these models to use depends on the threat model that is deemed to be realistic: whether we will be concerned with the possibility that evidence is correct in the presence of an external intruder who might have interfered with the protocol, or whether the medium is not considered to be so actively hostile but simply unreliable. Furthermore, the unreliability of the medium (or the power of participating agents over the medium) might conceivably make a difference, particularly on issues such as whether messages can be delivered to the wrong address.
The system is then described in the usual way, as follows:
)
The initial knowledge of the agents IKa will include their own private keys, and possibly keys shared with other agents. The initial knowledge of the medium will depend on the model of the medium. If it is simply an unreliable medium then it will simply hold messages that are passed to it, and hence its initial knowledge will be empty. However, if the medium can behave as a more active intruder then there may be some specific initial information, such as the private keys of compromised agents.
The non-repudiation property can require that occurrence of evidence.a.m (presented to the environment) provides a guarantee that some other message m′ must previously have been produced by b. This may be expressed as follows:
)
Since b cannot be relied upon to behave in accordance with the protocol, the message m′ might not have been issued by b directly as a complete message. However, m should still provide evidence that m′ was somehow issued by b, even if it was in a different form than the protocol expects.
For example, if a has the message {m}Private_Key(b) which has been signed by b using a private key unavailable to any agent other than b, then a is in possession of evidence that b issued m in some sense. However, it may have been sent as a component of a larger message or under further encryption, so the fact{m}Private_Key(b) might not have been transmitted as a message itself. The notation b sent m′ will be used to mean that m′ was transmitted by b, possibly as a component of a larger message (and not necessarily to the agent presenting the evidence):
)
where the contains relation is defined as follows: For all messages m, m′, and m″, and keys k:
-
m contains m
-
m′ contains m ⇒ m″.m′ contains m
-
m′ contains m ⇒ m′.m″ contains m
-
m′ contains m ⇒ k(m′) contains m
In the face of the threat model we are considering, this appears to be the strongest property that can be expressed for a non-repudiation protocol. In some sense if the message sent by b is going to be taken as evidence then it is incumbent upon b to issue it with care, and it would be unusual in practice for b to transmit it in any other form (though he should take care to ensure this does not occur by accident).
Example: the Zhou-Gollmann protocol
We will consider the modelling of a particular non-repudiation protocol. In fact this makes use of some additional features that require extensions to the model described above. The aim is for a to send a message m to b, and for the parties to obtain evidence that the message was sent and received. This protocol also aims to achieve fairness.
The message m is transferred in two stages: an encrypted form is first sent directly to b under some key k, and after a has received evidence of receipt from b the key k itself is sent via a trusted server. The server makes the key available via ftp, and both a and b have the responsibility to retrieve the key and the evidence that it was deposited by a.
Agent b should not be able to extract m until both of these messages have been received.
A cut-down version of the protocol, with the unsigned parts of the message omitted, is described as follows:
)
Zhou and Gollmann explain the elements of the protocol as follows:
-
a: originator of the non-repudiation exchange.
-
b: recipient of the non-repudiation exchange.
-
j: on-line trusted server providing network services accessible to the public.
-
m: message that is to be sent from a to b.
-
c: commitment (ciphertext) for message m, e.g. m encrypted under a key k. The point is that c in itself is not enough to identify the message m, but that c together with k is.
-
k: message key defined by a.
-
l is a label used to identify a particular protocol run. It should be unique to a single protocol run.
-
fNRO, fNRR, fSUB and fCON are flags used to identify the step of the protocol in which a particular message was generated.
-
SKi is a private signature key known only to its owner i; and SKj is the server’s private signature key.
The steps of the protocol are explained as follows:
-
1 With the first message, a sends a signed combination of c = k(m), a label l, and the recipient’s name b. b will use this as evidence that k(m) was sent in a run identified with l.
-
2 b responds with a signed record that c has been received in run l. This will provide evidence for a that k(m) was received.
-
3 a then sends the key k to the trusted server together with the label l.If a tries to cheat by sending the wrong key, then he will not obtain the evidence he requires, since k(m) and k′ will not provide evidence that m was sent.
-
4&5 Each of a and b can retrieve, by means of an ftp-get, a signed record from s that the key k associated with protocol run l has been deposited. Responsibility for retrieving this information rests with the agents themselves, to nullify a possible future claim that ‘the message was never received’. Thus both a and b can obtain evidence that the key k was made available to b.
The server only needs to handle relatively small messages, and make them available by ftp, so this protocol is appropriate even if the messages themselves are extremely large, since the server never has to handle them directly.
At the end of the protocol run, if a wishes to prove that the message
has been received, he presents )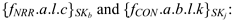
the first piece of evidence confirms that b received c, and the
second piece confirms that the key was deposited with the server, which means
that b has access to it, and hence to the message. The label l
in both pieces of evidence connects the two items k and c as being
associated with the same protocol run. This reasoning is really concerned with
two pieces of evidence, and is thus captured as two requirements on the system:
)
The non-repudiation of receipt property NRR(tr) is taken as the conjunction of these ] two implications. If the system provides both of these properties, then a has only to present his evidence to prove that b did indeed have access to the message m. The honest operation of the server means that a need only present evidence that the server received the correct message. The system then guarantees that this information is also available to b.
If b wishes to prove that the message was sent by a, he presents both pieces of evidence SKa(fNRO.b.l.c) and SKj(fCON.a.b.l.k): the first provides evidence that c was sent, and the second provides evidence that k was also sent, to the server. This treatment of evidence is again expressed as two trace requirements:
)
The non-repudiation of origin property NRO(tr) is defined as the conjunction of these two trace properties.
The CSP model of the system will have to include at least the two participants in the protocol and the server. It is also reasonable to allow the presence of other agents who are potential protocol participants, since the protocol is expected to be correct even in the presence of other users of the network. The ftp connection can be modelled as another channel ftp directly between the server and the participants. In fact this does not make any difference to correctness with respect to the properties above, but it justifies the informal argument that messages are available to the agents once they have arrived at the server, and underpins the claim that the properties above are appropriate.
The entire network is the parallel combination of these components:
)
This is illustrated in Figure 3.8.
)
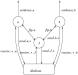Figure 3.8. Network for the Zhou-Gollmann non-repudiation protocol
The description of the participating agents is extended to permit receipt of facts along the ftp channel from Jeeves:
)
The server described by process Server accepts signed messages of the form of step 3 of the protocol, and makes them available via ftp. It is assumed that the server acts in accordance with its role in the protocol. It is therefore modelled as follows:
)
The server guarantees that any messages retrieved from it via ftp correspond to receipt of an appropriately signed fSUB message in accordance with the protocol.
The correctness requirements on the entire system are then
)
and
)
The protocol itself is not modelled explicitly within CSP. The descriptions of the agents allow correct execution of the protocol as possible behaviour. If the system meets these properties, then it proves that the evidence is sufficient to provide the guarantees we require, in the context of the server. The protocol can be seen as a pragmatic suggestion for how the participants might obtain the evidence they require, but the security property of the protocol rests more on the nature of the evidence than on the participants following the protocol itself.