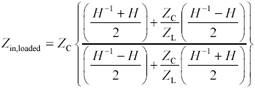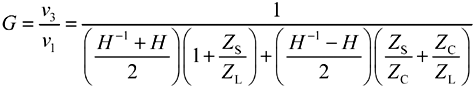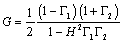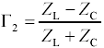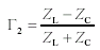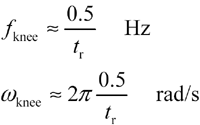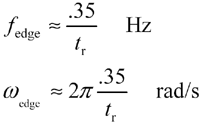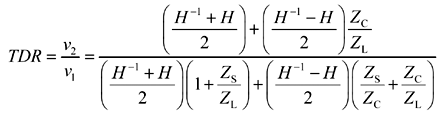- Signal Propagation Model
- Hierarchy of Regions
- Necessary Mathematics: Input Impedance and Transfer Function
- Lumped-Element Region
- RC Region
- LC Region (Constant-Loss Region)
- Skin-Effect Region
- Dielectric Loss Region
- Waveguide Dispersion Region
- Summary of Breakpoints Between Regions
- Equivalence Principle for Transmission Media
- Scaling Copper Transmission Media
- Scaling Multimode Fiber-Optic Cables
- Linear Equalization: Long Backplane Trace Example
- Adaptive Equalization: Accelerant Networks Transceiver
This chapter is from the book
This chapter is from the book
This chapter is from the book
3.3 Necessary Mathematics: Input Impedance and Transfer Function
The performance of the linear, time-invariant transmission circuit shown in Figure 3.3 depends on four crucial factors: the characteristic impedance of the line ZC [3.15], the raw one-way propagation function of the transmission line H [3.14], the source impedance ZS, and the load impedance ZL. All four of these complex phasor quantities vary with frequency. Although the figure is drawn representing a single-ended coaxial configuration the same considerations apply to any form of conductive transmission circuit.
)
Figure 3.3. A transmission line complete with source and load impedances may be modeled as a cascade of three two-port circuits.
The input impedance v2/i2 of a loaded transmission line is derived in Appendix C, “Two-Port Analysis.”
)
The gain G of the circuit of Figure 3.3, taking into account all the relevant loading effects and end-to-end reflections, is (see Appendix C)
)
|
where |
G is the overall system gain from the open-circuited output of the driver v1 to the load v3, |
|
ZS is the source impedance of the driver (Ω), |
|
|
ZL is the load impedance at the far end of the transmission structure (Ω), |
|
|
ZC is the characteristic impedance of the transmission structure (Ω), and |
|
|
H is the one-way propagation function of the raw, unloaded transmission structure [3.14]. |
Formulation [3.17] is most useful for analyzing the behavior of lumped-element and RC-mode transmission structures. An alternate form applies best for the analysis of the low-loss structures (LC, skin-effect, and dielectric-loss regions).
)
|
where |
G is the overall system gain from the open-circuited output of the driver v1 to the load v3, |
|
|
|
|
|
|
|
H is the one-way propagation function of the raw, unloaded transmission structure [3.14]. |
)
)
If your objective is the undistorted conveyance of a signal from source to load, then you must ensure that the propagation function [3.17 or 3.18] remains flat over the band of frequencies covering the bulk of the spectral content of your data signal. The requirement for “undistorted conveyance” is equivalent to asking that each transition arrive intact, at full size, without significant dispersion of the rising or falling edge, and without any lingering aftereffects, like reflections or ringing. Such a waveform is useful for first-incident-wave switching, meaning that the first edge arrives with sufficient fidelity to be immediately and reliably used.
On the other hand, if you are willing to wait a few round-trip times for your signal to settle, then you do not need your signals to arrive with first-incident-wave quality. You can in this case tolerate significant imperfections in the frequency response of your channel, all of which are cured by waiting for the steady-state condition to emerge, after which the signal may be reliably used. Waiting solves almost every signal integrity problem. If you can wait long enough, any transmission line will settle to a steady state. Of course, I assume the reason you are reading this book is that you cannot afford to wait! In that case, you have a direct interest in the gain flatness of the propagation function.
The bulk of the useful spectral content of a random data sequence spans a range from DC (zero frequency) up to a maximum upper bandwidth of
)
The knee frequency, fknee, is a crude estimate of the highest frequency content within a particular digital signal. Presuming the propagation function G [3.17] remains flat to within x percent over the range 0 < f < fknee, the expected distortion in the received waveform will be on the order of x percent.
The best assumption for the midpoint of the spectral content associated with the rising and falling edges of a digital signal is a little less than the maximum bandwidth:
)
A time-domain reflectometry (TDR) setup measures the gain from v1 to v2 (see Appendix C):
)
|
where |
TDR is the overall system gain from the open-circuited output of the driver v1 to the time-domain reflectometry observation point v2, |
|
ZS is the source impedance of the driver (Ω), |
|
|
ZL is the load impedance at the far end of the transmission structure (Ω), |
|
|
ZC is the characteristic impedance of the transmission structure (Ω), and |
|
|
H is the one-way propagation function of the raw, unloaded transmission structure [3.14]. |
The following sections detail the performance characteristics of each region and the means necessary to maintain acceptable flatness in [3.17] over the intended range of operation.
The step-response approximations for each region work best for transmission media with wide, well-defined regions. For example, the skin-effect approximation presented below represents the performance of Belden 8237 beautifully over a range of four orders of magnitude, from 105 to 109 Hz. As you approach the edge of each region, however, the step response begins to mutate into a new shape characteristic of the next region.
The modeling of complete systems, including arbitrary source and load impedances and combinations of operation in all regions, is considered at the end of this chapter.
-
The undistorted conveyance of a signal from source to load requires a propagation function that remains flat over a band of frequencies covering the bulk of the spectral content of the data signal.