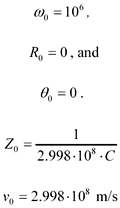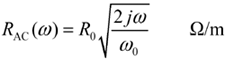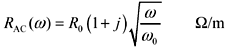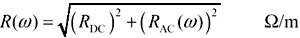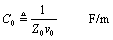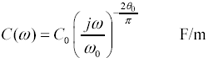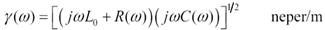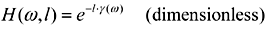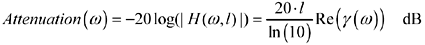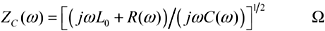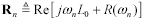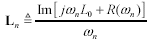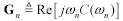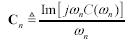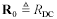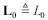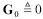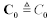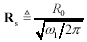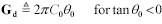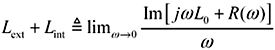Performance Regions
- Signal Propagation Model
- Hierarchy of Regions
- Necessary Mathematics: Input Impedance and Transfer Function
- Lumped-Element Region
- RC Region
- LC Region (Constant-Loss Region)
- Skin-Effect Region
- Dielectric Loss Region
- Waveguide Dispersion Region
- Summary of Breakpoints Between Regions
- Equivalence Principle for Transmission Media
- Scaling Copper Transmission Media
- Scaling Multimode Fiber-Optic Cables
- Linear Equalization: Long Backplane Trace Example
- Adaptive Equalization: Accelerant Networks Transceiver
This chapter is from the book
This chapter is from the book
This chapter is from the book
Figure 3.1 displays the propagation function of six distinct types of coaxial cabling, plus one typical pcb trace. The horizontal axis shows the operating frequency in units of Hz. The vertical axis shows cable attenuation in units of dB. Both axes use logarithmic scales.23
)
Figure 3.1. The attenuation curve for all copper transmission media is divided into distinct regions, with a characteristic relation in
each region between the attenuation a and frequency.
Each curve may be divided into distinct regions, with a characteristic shape to the loss function in each region. The hierarchy of regions, in order of increasing frequency, proceeds generally in the same order for all copper media:
-
RC region
-
LC region
-
Skin-effect region
-
Dielectric loss region
-
Waveguide dispersion region
Within each region the requirements for termination differ, as do the tradeoffs between length and speed. Remarkably, a common signal propagation model accurately describes almost any type of metallic transmission media across all four regions.
3.1 Signal Propagation Model
This model computes the transfer function and impedance of any forms of metallic cabling. It is appropriate for use with cables made in multiwire, ribbon, UTP, STP, or coaxial format. It also works for pcb traces, both striplines and microstrips, up to a frequency of approximately 10 GHz.
Table 3.1 describes the six parameters to the model, and further explanation is provided in the notes that follow.
Table 3.1. Parameters for Metallic Transmission Model
|
Name |
Meaning |
Units |
Ref |
|---|---|---|---|
|
RDC |
DC resistance of conductors |
Ω/m |
[2.37] |
|
ω0 |
Frequency at which AC line parameters are specified |
rad/s |
see notes |
|
R0 |
Real part of AC resistance at frequency ω0 (real part of zi) |
Ω/m |
[2.43] |
|
θ0 |
Angle formed by the real and imaginary parts of complex electric permittivity (arctg -ε′′/ε′) at frequency ω0, rad; for small angles, θ0 ≈ tan θ0 |
rad |
[2.73], [2.85] |
|
Z0 |
Characteristic impedance at frequency ω0 |
Ω |
[2.11] |
|
v0 |
Velocity of propagation (inverse of group delay) at frequency ω0 |
m/s |
[2.29] |
This model was developed over the course of many years, combining the best ideas from many versions of the international cabling standards with my own research.
This model is available in computer-executable form. It has been coded in MathCad 2000 syntax. A working version of the model along with a set of example spreadsheets and cable parameters is available through http://www.sigcon.com.
-
Frequency ω0 is assumed sufficiently high that the skin effect has substantially eliminated the internal inductance of the signal conductors, and the proximity effect has caused the distribution of current on the surface of the conductors to assume its high-frequency, magnetically dominated form, but not so high that you must concern yourself with non-TEM waveguide modes. In some geometrical arrangements such a setting is impossible. For example, a gigantic 3mm 50-ohm microstrip as typically used in microwave circuits might exhibit significant non-TEM behavior at frequencies as low as 10 GHz. Typical pcb geometries for digital circuits, being much smaller, enjoy the benefits of a much higher onset frequency for non-TEM behavior.
-
For simulations of data transmission systems operating above the onset of the skin effect, ω0 would ideally be located at or near one-half the transmission symbol frequency.
-
For simulations of data transmission systems operating entirely within the RC dispersion region a value for RDC and line capacitance C are required, but the other parameters may be ignored or set to default values:
These substitutions are equivalent to accepting C as a constant value independent of frequency and then setting the minimum possible value of L consistent with the speed of light.
-
If you have set ω0 commensurate with the rise/fall bandwidth of your digital signals, then parameter Z0 represents the average impedance over a section of transmission line with a delay comparable to the duration of one rising (or falling) edge. Parameter Z0 is assumed to be purely real—the model supplies the imaginary parts of the overall characteristic impedance ZC(ω).
-
Parameter RDC includes the total resistance of both outgoing and return conductors. For ribbon cables the total DC resistance sums the resistance of the outbound wire plus 1/N times the resistance of the N return wires. For twisted-pair cabling the total DC resistance is twice the resistance of either wire alone. For coaxial cables the total DC resistance is the sum of center conductor and shield resistances.
-
Parameter R0 similarly includes the total resistance of both outgoing and return conductors, with the path of current flow determined by the proximity effect.
-
Sometimes RDC is specified directly on the data sheet, in which case you should use that value instead of calculating it yourself from the wire sizes. Datasheet values take into account the resistivity of various alloys and coatings used in the construction of the conductors. Always use datasheet values when modeling copper-coated steel wire or tinned or silver-coated conductors.
-
Parameter θ0 models the effective dielectric loss for the mixture of insulating materials and air surrounding the conductors.
-
The model assumes uniform values for all parameters along the length of the transmission line.
-
The model does not take into account temperature variations. All parameters must be specified at their worst-case values.
-
The transmission line attenuation is maximized when you combine low Z0, low v0, large RDC, large R0, and large θ0.
)
Here are the model equations:
First use the specification of the real part of the skin-effect resistance, R0, which is specified only at a single frequency, to produce a resistance model covering a range of frequencies.
)
|
where |
R0 is the AC resistance of the wire at frequency ω0, in ohms, and |
|
RAC is the complex-valued impedance due to the combination of skin effect and proximity effect. |
The factor){kind=small}
indicates
that the skin-effect resistance grows proportional to the square root of frequency.
Another way to write the same equation is to substitute )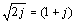
,
which leads to
)
The factor (1 + j) indicates that for all positive frequencies the real and imaginary parts of the complex skin-effect impedance are equal. You may also check that the real part of the complex skin-effect impedance equals R0 when ω = ω0.
Next we must model the crossover from DC resistance to AC resistance. I use a square-root-of-sum-of-squares type mixing function. This mixing function matches the measured skin-effect data presented in [28] and also produces the correct low-frequency value for the internal inductance of a round wire, 50 nH/m, given in [26] and [27].
)
The transmission line is characterized by a nominal external inductance L0 per meter, which I define as a constant, calculated from the characteristic impedance and velocity. This is the value of inductance measured at frequency ω0. Variations in inductance with frequency (which occur as part of the internal inductance) are incorporated into the imaginary part of R.
)
|
where |
Z0 is the nominal characteristic impedance at frequency ω0, and |
|
v0 is the velocity of propagation at frequency ω0. |
The transmission line is characterized by a nominal value of shunt capacitance C0 per meter, which is calculated from the characteristic impedance and velocity.
)
Formulas [3.5] and [3.6] are mathematical inverses of the telegrapher’s
relations )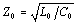
[2.30] and )
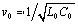[2.33].
Value [3.6] is next expanded into a frequency-varying model of the complex capacitance C(ω) of the transmission line. The imaginary part of jωC(ω) represents the capacitive reactance. The real part of jωC(ω) represents dielectric losses within the transmission line. The ratio of the real part of jωC(ω) to the imaginary part of jωC(ω) equals the dielectric loss tangent. A nonzero loss tangent induces a slow degradation in effective capacitance with increasing frequency.
)
The transmission-line propagation coefficient, per meter, is defined in numerous texts [29]:
)
The transfer function for a transmission line of length l meters is computed from the propagation coefficient,
)
The attenuation in dB is defined as the negative of the transfer gain in dB.
)
The characteristic impedance modeled as a function of frequency is
)
These equations correctly model the transfer function and impedance at low frequencies (in the dispersion-limited mode), mid-frequencies (in the skin-effect-limited mode), and at extremely high frequencies (in the dielectric-loss-limited mode).
In the mid-to-high frequency range the parameter RDC provides an amount of loss that is flat with frequency. The parameter R0 provides an amount of loss that grows (in dB) in proportion to the square root of frequency. The parameter θ0 provides an amount of loss that grows (in dB) in direct proportion to frequency. At all frequencies the magnitude and phase responses match to produce a causal, minimum-phase response.
-
The signal propagation model computes the transfer function and impedance of cables made in multiwire, ribbon, UTP, STP, or coaxial format. It also works for pcb traces, both striplines and microstrips, up to a frequency of approximately 10 GHz.
-
The parameter RDC provides an amount of loss that is flat with frequency.
-
The parameter R0 provides an amount of loss that grows (in dB) in proportion to the square root of frequency.
-
The parameter θ0 provides an amount of loss that grows (in dB) in direct proportion to frequency.
-
At all frequencies the magnitude and phase responses match to produce a causal, minimum-phase response.
3.1.1 Extracting Parameters for RLGC Simulators
Transmission-line parameters R, L, G, and C may be extracted from the expressions in the previous section.
Some simulators require a discrete table of parameters. Each row of the table represents the four values R, L, G, and C sampled at one particular frequency. The number of rows (frequency sample points) may be unlimited, with the frequencies spaced either linearly or exponentially on some kind of dense grid. The simulator interpolates between the listed points to do its work. Assuming you have the list of sample frequencies ωn in units of rad/s, Table 3.2 shows how to prepare the vectors R, L, G, and C from which you may prepare your table. The expressions properly account for the influence of the inductive component of skin effect (internal inductance) on the total inductance L and the influence of the imaginary part of C(ω) on G.
Other simulators expect you to provide values of only six parameters from which they extrapolate the full range of R, L, G, and C at all frequencies. I’m a little suspicious of these types of simulators because there is no consistent, standard way to perform the extrapolation. I have heard reports of some simulators generating noncausal waveforms. You should check carefully the step response of your simulator (especially under a condition with lots of dielectric loss but very little resistive loss) to make sure it gives you the correct causal dielectric response, as shown in Chapter 4, “Frequency-Domain Modeling.” Some don’t. One popular combination of parameters from which other values may be extrapolated appears in Table 3.3.
There is no consistent standard as to whether the value L0 includes the internal inductance or not. You’ll have to check the documentation of your simulator. The equations above assume it is not included in L0; therefore L0 in Table 3.3 just equals L0, which in my system of definitions is the external inductance. If you wish to include the internal inductance, then you should evaluate the total line inductance at a frequency well below the skin-effect onset (e.g., 1 rad/s) as shown in [3.12].
Table 3.2. R, L, G, and C Vectors Sampled at Frequencies ωn
|
Parameter |
Value |
Units |
|---|---|---|
|
Series resistance |
|
Ω/m |
|
Series inductance |
|
H/m |
|
Shunt conductance |
|
S/m |
|
Shunt capacitance |
|
F/m |
)
)
)
)
Table 3.3. Six R, L, G, and C Parameters from Which Other Values May Be Extrapolated
|
Parameter |
Value |
Units |
|---|---|---|
|
Series resistance |
|
Ω/m |
|
Series inductance |
|
H/m |
|
Shunt conductance |
|
S/m |
|
Shunt capacitance |
|
F/m |
|
Series skin-effect resistance |
|
Ω/(m-Hz1/2) |
|
Shunt conductance (dielectric loss) |
|
S/(m-Hz) |
)
)
)
)
)
)
)