1.3 Verification Methodology
A sound verification methodology starts with a test plan that details the specific functionality to verify so that the specifications are satisfied. A test plan consists of features, operations, corner cases, transactions, and so forth, such that the completion of verifying them constitutes verifying the specifications. To track progress against a test plan, a "scoreboarding" scheme is used. During scoreboarding, the items in the test plan are checked off when they are completely verified. In reality, it is infeasible to verify a set of specifications completely, in the sense that all bugs are uncovered. Thus, a measure of verification quality is desirable. Some commonly used coverage metrics are functional coverage and code coverage. Functional coverage approximates the percentage of functionality verified, whereas code coverage measures the percentage of code simulated. Neither functional coverage nor code coverage directly corresponds to how thoroughly bugs are eliminated. To compensate this shortcoming, bug rate and simulation cycles are widely used to gauge bug absence.
Besides a test plan, a verification methodology has to decide what language or languages should be used during verification. Verilog or VHDL are common design languages. Verification code often demands a language of its own, because the code is usually of a higher level and does not have to conform to strict coding style guidelines like design code. For example, arithmetic operators occur often in verification code but seldom in design code. On the contrary, design code usually has to be able to be synthesized, but verification code does not. Hence, an ideal verification language resembles a software language more than a hardware language. Popular verification languages include Vera, e, C/C++, and Java.
To study verification methodologies further, let's group verification methodologies into two categories: simulation-based and formal method-based verification. The distinguishing factor between the two categories is the existence or absence of vectors. Simulation-based verification methodologies rely on vectors, whereas formal method-based verification methodologies do not. Another way to distinguish simulation-based and formal method based verification is that simulation is input oriented (for example, the designer supplies input tests) and formal method verification is output oriented (for example, the designer supplies the output properties to be verified). There is a hybrid category called semiformal verification that takes in input vectors and verifies formally around the neighborhood of the vectors. Because the semiformal methodology is a combination of simulation-based and formal technology, it is not described separately here.
1.3.1 Simulation-Based Verification
The most commonly used verification approach is simulation-based verification. As mentioned earlier, simulation-based verification is a form of verification by redundancy. The variant or the alternative design manifests in the reference output. During simulation-based verification, the design is placed under a test bench, input stimuli are applied to the test bench, and output from the design is compared with reference output. A test bench consists of code that supports operations of the design, and sometimes generates input stimuli and compares the output with the reference output as well. The input stimuli can be generated prior to simulation and can be read into the design from a database during simulation, or it can be generated during a simulation run. Similarly, the reference output can be either generated in advance or on the fly. In the latter case, a reference model is simulated in lock step with the design, and results from both models are compared.
Before a design is simulated, it runs through a linter program that checks static errors or potential errors and coding style guideline violations. A linter takes the design as input and finds design errors and coding style violations. It is also used to glean easy-to-find bugs. A linter does not require input vectors; hence, it checks errors that can be found independent of input stimuli. Errors that require input vectors to be stimulated will escape linting. Errors are static if they can be uncovered without input stimuli. Examples of static errors include a bus without a driver, or when the width of a port in a module instantiation does not match the port in the module definition. Results from a linter can be just alerts to potential errors. A potential error, for example, is a dangling input of a gate, which may or may not be what the designer intended. A project has its own coding style guidelines enforced to minimize design errors, improve simulation performance, or for other purposes. A linter checks for violations of these guidelines.
Next, input vectors of the items in the test plan are generated. Input vectors targeting specific functionality and features are called directed tests. Because directed tests are biased toward the areas in the input space where the designers are aware, bugs often happen in areas where designers are unaware; therefore, to steer away from these biased regions and to explore other areas, pseudorandom tests are used in conjunction with directed tests. To produce pseudorandom tests, a software program takes in seeds, and creates tests and expected outputs. These pseudorandomly generated tests can be vectors in the neighborhood of the directed tests. So, if directed tests are points in input space, random tests expand around these points.
After the tests are created, simulators are chosen to carry out simulation. A simulator can be an event-driven or cycle-based software or hardware simulator. An event simulator evaluates a gate or a block of statements whenever an input of the gate or the variables to which the block is sensitive change values. A change in value is called an event. A cycle-based simulator partitions a circuit according to clock domains and evaluates the subcircuit in a clock domain once at each triggering edge of the clock. Therefore, event count affects the speed a simulator runs. A circuit with low event counts runs faster on event-driven simulators, whereas a circuit with high event counts runs faster on cycle-based simulators. In practice, most circuits have enough events that cycle-based simulators out-perform their event-driven counterparts. However, cycle-based simulators have their own shortcomings. For a circuit to be simulated in a cycle-based simulator, clock domains in the circuit must be well defined. For example, an asynchronous circuit does not have a clear clock domain definition because no clock is involved. Therefore, it cannot be simulated in a cycle-based simulator.
A hardware simulator or emulator models the circuit using hardware components such as processor arrays and field programmable gate arrays (FPGAs). First, the components in a hardware simulator are configured to model the design. In a processor array hardware simulator, the design is compiled into instructions of the processors so that executing the processors is tantamount to simulating the design. In an FPGA-based hardware acceleration, the FPGAs are programmed to mimic the gates in the design. In this way, the results from running the hardware are simulation results of the design. A hardware simulator can be either event driven or cycle based, just like a software simulator. Thus, each type of simulator has its own coding style guidelines, and these guidelines are more strict than those of software simulators. A design can be run on a simulator only if it meets all coding requirements of the simulator. For instance, statements with delays are not permitted on a hardware simulator. Again, checking coding style guidelines is done through a linter.
The quality of simulating a test on a design is measured by the coverage the test provides. The coverage measures how much the design is stimulated and verified. A coverage tool reports code or functional coverage. Code coverage is a percentage of code that has been exercised by the test. It can be the percentage of statements executed or the percentage of branches taken. Functional coverage is a percentage of the exercised functionality. Using a coverage metric, the designer can see the parts of a design that have not been exercised, and can create tests for those parts. On the other hand, the user could trim tests that duplicate covered parts of a circuit.
When an unexpected output is observed, the root cause has to be determined. To determine the root cause, waveforms of circuit nodes are dumped from a simulation and are viewed through a waveform viewer. The waveform viewer displays node and variable values over time, and allows the user to trace the driver or loads of a node to determine the root cause of the anomaly.
When a bug is found, it has to be communicated to the designer and fixed. This is usually done by logging the bug into a bug tracking system, which sends a notification to the owner of the design. When the bug is logged into the system, its progress can be tracked. In a bug tracking system, the bug goes through several stages: from opened to verified, fixed, and closed. It enters the opened stage when it is filed. When the designer confirms that it is a bug, he moves the bug to the verified stage. After the bug is eradicated, it goes to the fixed stage. Finally, if everything works with the fix, the bug is resolved during the closed stage. A bug tracking system allows the project manager to prioritize bugs and estimate project progress better.
Design codes with newly added features and bug fixes must be made available to the team. Furthermore, when multiple users are accessing the same data, data loss may result (for example, two users trying to write to the same file). Therefore, design codes are maintained using revision control software that arbitrates file access to multiple users and provides a mechanism for making visible the latest design code to all.
The typical flow of simulation-based verification is summarized in Figure 1.4. The components inside the dashed enclosure represent the components specific to the simulation-based methodology. With the formal verification method, these components are replaced by those found in the formal verification counterparts.
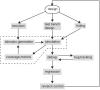
Figure 1.4 Flow of simulation-based verification
1.3.2 Formal Method-Based Verification
The formal method-based verification methodology differs from the simulation-based methodology in that it does not require the generation of test vectors; otherwise, it is similar. Formal verification can be classified further into two categories: equivalence checking and property verification.
Equivalence checking determines whether two implementations are functionally equivalent. Checking equivalence is infeasible using a simulation-based methodology because there are practically an infinite number of vectors in the input space. During formal verification, the decision from a equivalence checker is clear-cut. However, industrial equivalence checkers have not yet reached the stage of turnkey solution and often require the user to identify equivalent nodes in the two circuits to limit the input search space for the checkers. These user-identified equivalent nodes are called cut points. At times, a checker can infer equivalent nodes from the node names.
Two basic approaches are behind equivalence checking. The first approach searches the input space in a systematic way for an input vector or vectors that would distinguish the two circuits. This approach, called SAT (satisfiability), is akin to automatic test pattern generation algorithms. The other approach converts the two circuits into canonical representations, and compare them. A canonical representation has the characteristic property that two logical functions are equivalent if and only if their respective representations are isomorphic—in other words, the two representations are identical except for naming. A reduced ordered binary decision diagram is a canonical representation. Binary decision diagrams of two equivalent functions are graphically isomorphic.
Equivalence checking is most widely used in the following circumstances:
- Compare circuits before and after scan insertion to make sure that adding scan chains does not alter the core functionality of the circuit.
- Ensure the integrity of a layout versus its RTL version. This is accomplished by first extracting from the layout a transistor netlist and comparing the transistor netlist with the RTL version.
- Prove that changes in an engineering change order (ECO) check-in are restricted to the scope intended. This is done by identifying the changed regions in the circuits.
If an equivalence check fails, the checker generates an input sequence of vectors that, when simulated, demonstrates the differences between the two circuits. From the waveforms, the user debugs the differences. A failure can result from a true error or an unintended boundary condition. An unintended boundary condition arises when the scan circuitry is not disabled. Then a checker will generate a sequence of vectors that runs the postscan circuit in test mode while running the prescan circuit in normal operating mode. Surely these two circuits are not equivalent under this input sequence. Therefore, when comparing a prescan circuit and a postscan circuit, the postscan circuit must be configured in normal operating mode.
The other type of formal verification is property checking. Property checking takes in a design and a property which is a partial specification of the design, and proves or disproves that the design has the property. A property is essentially a duplicate description of the design, and it acts to confirm the design through redundancy. A program that checks a property is also called a model checker, referring the design as a computational model of a real circuit. Model checking cast in the light of the basic verification principle is visualized in Figure 1.3 (B).
The idea behind property checking is to search the entire state space for points that fail the property. If a such point is found, the property fails and the point is a counterexample. Next, a waveform derived from the counterexample is generated, and the user debugs the failure. Otherwise, the property is satisfied. What makes property checking a success in industry are symbolic traversal algorithms that enumerate the state space implicitly. That is, it visits not one, but a group of points at a time, and thus is highly efficient.
Even though symbolic computation has taken a major stride in conquering design complexity, at the time of this writing only the part of the design relevant to the property should be given to a property verifier, because almost all tools are incapable of automatically carving out the relevant part of the design and thus almost certainly will run into memory and runtime problems if the entire design is processed.
Furthermore, the power and efficiency of a property verifier is highly sensitive to the property being verified. Some properties can be decided readily whereas others will never finish or may not even be accepted by the tool. For example, some property verifiers will not accept properties that are unbound in time (for example, an acknowledgment signal will eventually be active). A bound property is specified within a fixed time interval (for example, an acknowledgment signal will be active within ten cycles).
A failure can result from a true design bug, a bug in the property or unintended input, or state configurations. Because a property is an alternative way of expressing the design, it is as equally prone to errors as the design. A failure can be caused by unintended input or state configurations. If the circuit under verification is carved out from the design, the input waveforms to the circuit must be configured to be identical to them when the circuit is embedded in the design. Failure to do so sends unexpected inputs (for example, inputs that would not occur when the circuit is a part of the design) to the circuit, and the circuit may fail over these unexpected inputs because the circuit has not been designed to handle them. To remove unintended configurations from interfering with property verification, the inputs or states are constrained to produce only the permissible input waveforms. Underconstraining means that input constraining has not eliminated all unexpected inputs, and this can trigger false failures. Overconstraining, which eliminates some legal inputs, is much more dangerous because it causes false successes and the verifier will not alert the user.
Some practical issues with property verifiers include long iteration times in determining the correct constraining parameters, and debugging failures in the properties and in the design. Because only a portion of the design is given to the property verifier, the environment surrounding that portion has to be modeled correctly. Practical experience shows that a large percentage of time (around 70 percent) in verification is spent getting the correct constraints. Second, debugging a property can be difficult when the property is written in a language other than that of the design (for instance, the properties are in SystemVerilog whereas the design is in Verilog). This is because many property verifiers internally translate the properties into finite-state machines in Verilog, and verify them against the design. Therefore, the properties are shown as the generated machine code, which is extremely hard to relate to signals in the design or is hard to interpret its meaning. Finally, debugging failures in a property has the same difficulty as any other debugging.
As an alternative to a state space search in verifying a property, the theorem-proving approach uses deductive methods. During theorem proving, a property is specified as a mathematical proposition and the design, also expressed as mathematical entities, is treated as a number of axioms. The objective is to determine whether the proposition can be deduced from the axioms. If it can, the property is proved; otherwise, the property fails. A theorem prover is less automatic than a model checker and is more of an assistance to the user. The user drives the tool to arrive at the proposition by assembling relevant information and by setting up intermediate goals (in other words, lemmas), whereas the tool attempts to achieve the intermediate goals based on the input data.
Effective use of a theorem prover requires a solid understanding of the internal operations of the tool and a familiarity with the mathematical proof process. Although less automatic, efficient usage of a theorem prover can handle much larger designs than model checkers and requires less memory. Furthermore, a theorem prover accepts more complex properties. For example, a theorem prover can allow the properties written in higher order logic (HOL) whereas almost all model checkers only accept first-order logic and computation tree logic or their variants. HOL is more expressive than first-order logic and enables a concise description of complex properties.
A typical flow of formal verification is shown in Figure 1.5. Remember that the components in this diagram replace the components inside the dashed box of Figure 1.4. Although formal verification does not require test vectors, it does require a test bench that configures the circuit in the correct operational mode, such as input constraining.
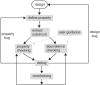
Figure 1.5 A typical flow of formal verification