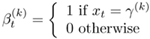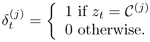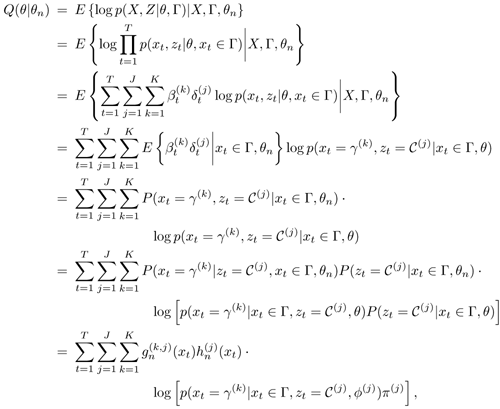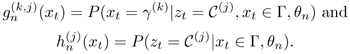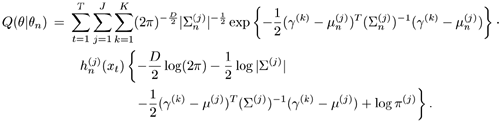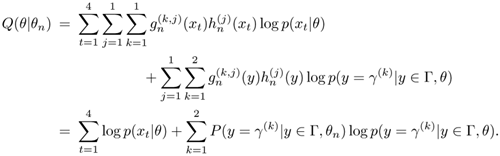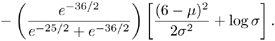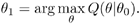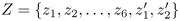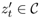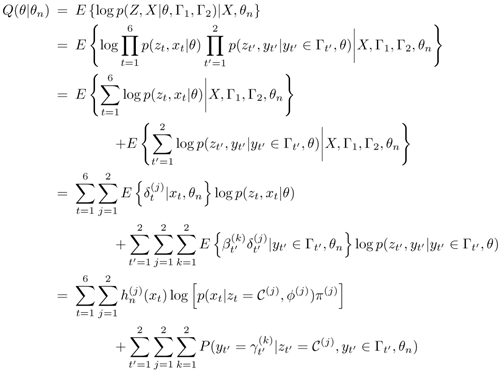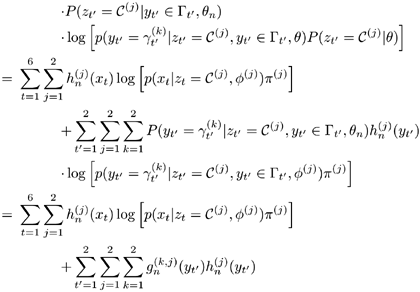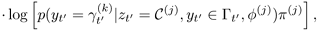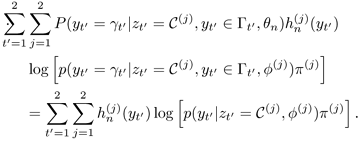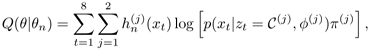- Introduction
- Traditional Derivation of EM
- An Entropy Interpretation
- Doubly-Stochastic EM
- Concluding Remarks
This chapter is from the book
This chapter is from the book
This chapter is from the book
3.4 Doubly-Stochastic EM
This section presents an EM-based algorithm for problems that possesses partial data with multiple clusters. The algorithm is referred to as as a doubly-stochastic EM. To facilitate the derivation, adopt the following notations:
-
X = {xt ∊ RD; t = 1,..., T } is a sequence of partial-data.
-
Z = {zt ∊ C; t = 1, . . . , T} is the set of hidden-states.
-
C = {C(1), . . . ,C(J)}, where J is the number of hidden-states.
-
Г = {γ(1)), . . . , γ(K)} is the set of values that xt can attain, where K is the number of possible values for xt.
Also define two sets of indicator variables as:
)
and
)
Using these notations and those defined in Section 3.2, Q(θ|θn) can be written as
where
)
If θ defines a GMM—that is, θ = {π(j), μ(j), )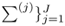
— then
)
3.4.1 Singly-Stochastic Single-Cluster with Partial Data
This section demonstrates how the general formulation in Eq. 3.4.1 can be applied to problems with a single cluster and partially observable data. Referring to Example 2 shown in Figure 3.3(b), let X = {x1, x2 x3, x4, y} = {1, 2, 3, 4, {5 or 6}} be the observed data, where y = {5 or 6} is the observation with missing information. The information is missing because the exact value of y is unknown. Also let z ∊ Г, where Г = {γ(1), γ(2)} = {5, 6}, be the missing information. Since there is one cluster only and x1 to x4 are certain, define θ ≡ {μ,σ2}, , set π(1) = 1.0 and write Eq. 3.4.1 as
Note that the discrete density p(y = γ((k)|y ∊ Г, θ) can be interpreted as the product of density p(y = γ(k)|y ∊ Г) and the functional value of p(y|θ) at y = γ(k) as shown in Figure 3.7.
)
Figure 3.7 The relationship between p(y|θ0), p(y|y ∊ Г), p(y|y ∊ Г, θ0), and P(y = γ(k) |y ∊ Г, θ0), where Г = {5, 6}.
Assume that at the start of the iterations, n = 0 and )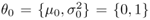
} = {0, 1}. Then, Eq. 3.4.2 becomes
)
In the M-step, compute θ1 according to
)
The next iteration replaces θ0 in Eq. 3.4.3 with θ1 to compute Q(θ|θ1). The procedure continues until convergence. Table 3.4 shows the value of μ and σ2 in the course of EM iterations when their initial values are μ0 = 0 and )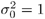
. Figure 3.8 depicts the movement of the Gaussian density function specified by μ and σ2 during the EM iterations.
Table 3.4. Values of μ and σ2 in the course of EM iterations. Data shown in Figure 3.3(b) were used for the EM iterations.
|
Iteration (n) |
Q(θ|θn) |
μ |
σ2 |
|---|---|---|---|
|
0 |
−∞ |
0.00 |
1.00 |
|
1 |
-29.12 |
3.00 |
7.02 |
|
2 |
-4.57 |
3.08 |
8.62 |
|
3 |
-4.64 |
3.09 |
8.69 |
|
4 |
-4.64 |
3.09 |
8.69 |
|
5 |
-4.64 |
3.09 |
8.69 |
)
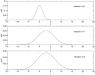Figure 3.8 Movement of a Gaussian density function during the EM iterations. The density function is to fit the data containing a single
cluster with partially observable data.
3.4.2 Doubly-Stochastic (Partial-Data and Hidden-State) Problem
Here, the single-dimension example shown in Figure 3.9 is used to illustrate the application of Eq. 3.4.1 to problems with partial-data and hidden-states. Review the following definitions:
-
X = {x1, x2,..., x6, y1, y2} is the available data with certain {x1,..., x6} and uncertain {y1, y2} observations.
-
where zt and 
is the set of hidden-states.
-
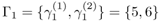and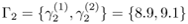 
such that y1 ∊ Г1 and y2 ∊ Г2 are the values attainable by y1 and y2, respectively.
-
J = 2 and K = 2.
)
)
)
)
){kind=link}
)
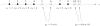Figure 3.9 Single-dimension example illustrating the idea of hidden-states and partial-data.
Using the preceding notations results in
)
)
where )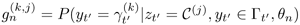
is the posterior probability that yt' is equal to )
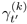given that yt' is generated by cluster C(j). Note that when the values of y1 and y2 are certain (e.g., it is known that y1 ═┴ 5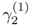, and )
and )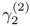
become so close that we can consider y2 = 9), then K = 1 and Г1 = {γ1} = {5} and Г2 = {γ2} = {9}. In such cases, the second term of Eq. 3.4.4 becomes
Replacing the second term of Eq. 3.4.4 by Eq. 3.4.5 and seting x7 = y1 and x8 = y2 results in
)
which is the Q-function of a GMM without partially unknown data with all observable data being certain.