Euclid in the Rainforest: Discovering Logic and Math
An Introduction to Logic and Proof
"Number theory effortlessly produces innumerable problems, which have a sweet, innocent air about them—like tempting flowers."
"Flowers?"
"Mm-hmm." He also says that, "it swarms with bugs waiting to bite the flower lovers who, once bitten, are inspired to excesses of effort."
—Daphne Clair quoting Barry Mazur, Summer Seduction
The mix of fragrances from blooming yucca, violets, red jasmine, and frangipani carried on the vapors of rising mists above the humid Orinoco River are intoxicating. It is the perfume of the Venezuelan rainforests, where tobacco, banana and coffee grow wild and barbets call so loudly you can hardly hear nearby rapids. I was there at a time when one could still get a doctorate in anthropology from stories of undiscovered indigenous tribes in one of the last unknown corners of the world, a time when roads connecting Venezuelan cities and towns were unpaved or didn't exist at all. Young with mettle in adventure and eager for cerebral exercise, it was there on the edges of the primal rainforest that I first stumbled over notions of logic and what it means to believe a proof.
Before I knew anything about what anthropologists were or what they did, I read Hamilton Rice's accounts of his encounters with the Yanomami Indians living along the Orinoco River in southern Venezuela and decided to travel to the remote Venezuelan village of La Esmeralda on my own. It was 1960, several years before Napoleon Chagnon's best-selling book Yanomamo: The Fierce People was published.1 I got the required inoculations, bought malaria pills, and went to the Venezuelan consulate in New York to apply for a visa.
I was disappointed to learn that it would take two months to process my visa. Thinking it would be faster to get a visa from a small consulate near Venezuela, I flew to Aruba, which is just sixteen miles north of the coast of Venezuela. I arrived there on a Sunday to find that the consulate was open only on Wednesdays. I waited three days at the edge of boredom. At 9:00 a.m. on Wednesday, I walked up the two flights of creaking stairs in a dark, alcohol-reeking, wooden office building. The sign outside the consul's office door clearly indicated that the office would be open from 9:00 to noon. I waited. At about 11:15, a Sydney Greenstreet look-alike in a white suit and Panama hat arrived smelling of rum. He was the Venezuelan consul.
"Can I help you?" he asked scornfully.
"I would like a visa for Venezuela," I said, wondering if he would ask me why.
"Yes, I can get you a visa, but it will take two months!" he said with a snickering smile.
Defeated by the thought that I had traveled a thousand miles to a barren island for the same deal that I could have had in New York, I thought of the crazy idea of getting a fisherman to bring me across the short stretch of water separating Aruba from the mainland. However, the consul's snicker gave me hope, so I asked if there was any other way to speed up the process.
"Certainly!" he said. "For five dollars, you could have it today!"
I placed a five-dollar bill on his desk. "Your passport please," he demanded. He pulled out a mechanical stamp machine from the center drawer of his desk, found an empty page in my passport, and stamped it with a visa to Venezuela. I took the next flight to Caracas.
An Englishman a bit older than me sat beside me on the plane. "Have you ever been to Caracash?" he asked with a proper English accent embroidered with an S-lisp while extending his greeting hand. "My name is Roger Hooper," he continued with a look suggesting that I should have heard the name before. Upon learning my plans to travel to the Orinoco River, he proceeded to tell me about his dream of doing the same. He proceeded to tell me about Joseph Conrad's Heart of Darkness, as if I had never heard of it. I was absorbed in his story almost as much as he was until a lightning storm struck without warning. Passengers around us anxiously clutched at armrests as we bounced from air pocket to air pocket. The plane pitched forward and backward, rocked from side to side, and shook with each threatening lightning bolt as it passed through torrential rain and foreboding darkness. Roger casually went on with his story, unaware that I was no longer listening. The plane came to an abrupt stop, listing to the left while torrential rain continued to pour over the windows; I could see nothing outside.
My neighbor continued talking as if nothing had happened. A minute passed before the pilot announced that, though the plane had come to a safe landing, it would not be easy to disembark. The plane was in water up to its belly. The pilot had chosen to emergency-land his plane in the safety of water rather than risk an airport landing close to rugged mountains in a severe storm. We disembarked on a makeshift ramp constructed by curious emergency personnel. As we were coming off the plane, Roger did not say a word about the event, nor a word about the inconvenience of our waterlogged luggage. He continued to lisp about the Congo, but I was processing almost nothing of what he was saying and was beginning to be annoyed. I was going to the Orinoco River, not the Congo. He said, in his first reference to our aircraft drama, that he, too, was headed for the Amazon on an adventure far more exciting than any emergency landing.
When I finally did get around to telling him my name, he blankly announced that he knew of a mathematician by that last name and asked if there was any relation. I had grown used to saying "he's my brother" whenever people asked the same question. At that, he said that he also majored in mathematics and unleashed the grand story of Fermat and his Last Theorem, the famous theorem that says that xn + yn = zn has no nonzero whole-number solutions for x, y, and z when n is greater than 2. He could make the Caracas airport flight schedule seem like a Noel Coward play. Roger explained the theorem with the math embroidered into a fabric of supporting characters. In fact, all we really know for sure is that when Fermat died, his son Samuel discovered a copy of a translation of Diophantus's Arithmetica in the library with a marginal note in his father's handwriting: "I have discovered a truly remarkable proof, which this margin is too small to contain."
Few of us are taught the rules of logic or principles of proof. Even mathematicians seem to innocently learn them indirectly through instinctive knowledge and experience of language, just as the toddler does in acquiring the elements of grammar. However, when we intellectually reflect on logic and proof, what they are and what they do, we tend to agree that, formally, a proof consists of a finite collection of well-formed statements linking back, by rules of inference, to elementary assumptions. For example, if we want to prove that the base angles of an isosceles triangle2 are equal, we must start somewhere. Proof means that belief is universal. If Euclid's proofs are to be accepted, all parties must agree that "there is a unique line passing through any two points," which is exactly Euclid's first elementary assumption. This assumption, together with four others, forms a footing to support a superstructure of Euclid's geometry.
Margin notes were typical for Pierre Fermat. He was a lawyer and judge in Toulouse, and, though considered the greatest mathematician of his day, he did mathematics only in his spare time. He didn't publish his works, but he preferred to write them as gifted letters to friends and professional mathematicians. Pierre frequently wrote his thoughts in the margins of his books, often while listening to briefs at court. But Roger painted a fanciful picture of Samuel, his appearance as a young man with bulging eyes, an unusually long but handsome nose, a sullen face, and a tragic mouth that always seemed to be lamenting something lost. According to Roger, Samuel was asleep in his library when a howling wind blew a window open. The window frame knocked Diophantus's Arithmetica off a sill, face down, and opened to a page biased by a pressed dry rose. And there it rested until Samuel lit a candle to see the short comment responsible for a great deal of modern number theory.
When Roger finished his story, he suggested that we should head for La Esmeralda together. I was only eighteen and Roger was ten years older. He already had a receding hairline at the sides of his head and the beginnings of a double chin that he was trying to hide behind a newly cultured beard. And, though he was definitely peculiar, insensitive, and possibly even crazy, I wanted someone to accompany me on a journey that was beginning to frighten me. Roger had the annoying habit of cracking his knuckles at odd times when he was silent. He would dovetail fingers from both hands, turn his palms outward, and push both hands forward to the sound of multiple cracks. However, he was fluent in Spanish, and I needed a translator. I had no idea what trouble I was about to get into and naively thought I could make my way into the jungle on a few provisions, a tent, and malaria pills.
At his suggestion, we hitchhiked a ride with a Venezuelan army convoy traveling five hundred miles into the jungle along dirt roads to Cabruta on the Orinoco River. It was an innocent time, when two foreign civilians could unofficially still do such things. The convoy would go no further than Cabruta, for there was no bridge to cross the river, but we accepted the ride, thinking that at least we would get to the Orinoco, even if it were a thousand miles downstream from La Esmeralda. After about two hundred and fifty miles, we came to a washed-out mountain switchback. A canvas-covered army vehicle was tottering over a precipice and about to fall into a ravine several hundred feet below. It was nighttime and lightly raining; the bugs were out to devour anyone stupid enough to stand on the road unprotected. More than twenty soldiers took positions to push the vehicle onto a more solid road surface, and my position was at the right taillight, the main attraction for mosquitoes and diving beetles in the area. My clothes were covered with tightly gripping diving beetles. Roger was thrilled. This was the adventure he had come for.
We gave up for the night when the rain started to come down heavily. The road was impassible, so we slept huddled under the canvases of the trucks. I can't recall why the tottering vehicle was not tethered or winched to one of the other trucks, but it wasn't. In the morning, the sun rose above several isolated mists that passed with gentle breezes. A choir of birds awakened us with what seemed to be a thousand different simultaneous songs. Several of us with stiff bodies from sleeping in awkward positions rose with the sun to hear and feel the road give way, sending the tottering vehicle to its grave at the bottom of the ravine. I looked out in time to see Roger standing on the road, peering down at the fallen truck, laughing.
A cook prepared breakfast of potatoes and eggs on a propane stove, while a small group of three young, tough soldiers and a platoon sergeant argued about how to salvage the fallen vehicle. Miguel Ramos, the sergeant, was more concerned with the contents of the truck. Eating peaches from a can, he gave a stout order to salvage the contents. So several fifty-five gallon oil drums and dozens of sealed wooden crates marked in alphanumeric code were hoisted to the road, while Jesus and two other soldiers whose names I no longer recall continued to argue about how to salvage the truck itself.
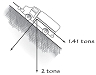
The truck weighed two tons, and the winch cable capacity was only one ton. I volunteered to say that if the truck could be straightened out, it would take only about 1.4 tons of cable tension to winch the truck back to the road.3 At the time, I thought it to simply be an academic point, since the cable's capacity was still smaller than what was needed to hoist the entire truck. But I had to convince the group that they needed a winch with only a 1.4-ton capacity.
I used a stick to draw a diagram in the dirt, trying to explain the trigonometry of forces involved while a conspicuously colorful object, far off in the distance over the steep hillside of wildflowers, distracted my audience. I stopped my explanation to join the diversion.
It was a wild apricot tree two hundred feet away in the middle of the field, surrounded by tall, particularly beautiful flowers with very tall pistils and alternating red and black petals. In this wonderful field of yellow and blue flowers, that unusual red-and-black one was the only one swarmed with bees. No one had ever seen such a flower. For several minutes, we were captivated.
We approached the tree to find that what we thought was one apricot tree was actually two intertwined trees. As we stuffed our pockets with wild apricots, an idea leaped in front of me: If we could get the winch on the fallen truck to work, we could intertwine two winches to work together with a capacity of two tons—more force than necessary! The answer depended on whether the fallen truck would start. Luckily, a tree had broken the fall as the truck rolled backward, so the only damage was to the rear end. Jesus started the truck and got the winch working. The rest was easy. Entwined cables connected the fallen truck to a tethered truck on the road. The two winches synchronically rewound, slowly pulling the fallen truck up the dirt incline. A small piece of entirely theoretical trigonometry solved a thoroughly physical problem, a testament to the power of mathematics. The operation worked so smoothly that Jesus asked me to explain how I made my calculations. He was hooked.
And so was I. For the remainder of our trip, Roger enthusiastically taught us applications of trigonometry and beguiling mathematics.
Mathematics was not always what it is today. Its formal rigor and structure did not always rely on finite collections of well-formed statements linking back, by rules of inference, to elementary assumptions. No, in Thales's time (around 600 b.c., a half-century before Pythagoras), when Western mathematics inherited a fortune in concrete applications from a thousand years of Babylonian and Egyptian calculations, when abstract so-called theorems in need of proof were beginning to surface on the mathematical horizons, mathematical proof was far more relaxed and casual. Arguments were persuasive but not as rigorous as those that would come in the next three hundred years, before Euclid, when the ideas for structured proof based on elementary assumptions emerged.
One of the earliest existing histories of geometry is one that comes to us from Proclus, a philosopher and historian who summarized an earlier history by Eudemus of Rhodes. According to several historians, from Proclus to Plutarch, Thales of Miletus introduced abstract geometry, a new phenomenon that was to excite further Greek creations.4 The Rhind papyrus, now in the British Museum, is a handbook of practical problems dating from about 1550 b.c. The papyrus calls itself "a guide to accurate reckoning of entering into things, knowledge of existing things all." Everything in the papyrus is stated in terms of specific numbers and nothing is generalized. Rectangles are measured, but only when their sizes are specified; right-angled triangles5 mark out areas only when the sides are specified. During Thales's lifetime, Egyptian mathematics was still relying on tables to solve problems from surveying to banking, just as modern bankers rely on tables or computer programs to compute mortgage payments. Thales's revelation was that there are precise relationships between parts of figures and that such relationships enable one to find one part by knowing others.
It may seem obvious to us that the height of a right triangle, whose hypotenuse is, say, five units long, absolutely depends on the length of the base. Equally obvious is the thought that one can know what that dependency is. We know that the height is the square root of five minus the square of the length of the base. But this was not something in the Egyptian schoolboy's textbook.
Modern Western mathematics began with Thales. We are told that he is the first to "demonstrate" the following:
The circle is bisected by its diameter.
The base angles of an isosceles triangle are equal.
The vertical angles of two straight lines are equal.
The right-angled triangle can be inscribed in a circle in such a way that its hypotenuse coincides with the diameter and its right angle sits on the circle.
These are extraordinary statements about every circle and every isosceles triangle.
He must have known that the sum of the angles of a triangle is 180°, or the sum of two right angles. The persuasive argument of his time must have been something like this: Any triangle can be split into two right angles simply by dropping a perpendicular from the largest angle to the side opposite that largest angle.
Take any one of these two right triangles, inscribe it in a circle, and connect the right angle to the center of the circle.
You now have two isosceles triangles. But Thales knew that the base angles of an isosceles triangle are equal. Since angle ADB is a right angle, we see that the sum of all three angles must be two right angles because angle ADC + angle CDB equals one right angle, and angle DAC + angle DBC = angle ADC + angle CDB.
This could be one of the earliest examples of mathematical persuasion, but not a proof in the modern sense of the word because it simply follows a picture without inferences from axioms or established statements. To make the argument into a proof, we must infer the argument from some collection of established statements that can never be disputed. What are those established statements? We used the fact that the points of the circle are equidistant from the center to know that the triangles are isosceles. We used the fact that the base angles of an isosceles triangle are equal. And we used the fact that a right-angled triangle could be completely inscribed in a circle whose diameter is equal to the hypotenuse of the triangle. These were all facts known to Thales.
We might accept the statement that points of the circle are equidistant from its center as part of the definition of a circle. However, the statement that base angles of an isosceles triangle are equal is much harder to accept. It's not obvious. It relies on an argument composed of several more elementary statements, one of which is that two points determine a unique line, and another that a circle of given center and radius can always be constructed.
These last two statements seem very strongly acceptable—so acceptable that we might accept them without argument. We could simply establish these as true and "prove" the statement that the sum of the angles of any triangle is two right angles by inferring it from the established statements. However, we must be careful. Suppose that the two established statements have hidden conflicts. What if, after one thousand years of building arguments on arguments that use these statements as foundations, a contradiction is implied? We must be sure that such a thing can never happen. In other words, we must be sure that the statements are independent of each other.
This means that the negation of one cannot be logically derived from the other. Discovering this was the great achievement of early Greek mathematicians in the three hundred year span between Thales and Euclid. When Thales generalized the practical mathematics of the Egyptians, other mathematicians made other general discoveries. The Pythagorean School discovered relationships between the sizes of the sides of right triangles. Eventually, the work turned to organizing general statements, systematizing and ordering statements in a network of inferential statements, one following from another.
Although mathematics appears to be built from a collection of self-evident assumptions, it does not develop directly from them. Thales had no established postulates, yet his arguments are as persuasive as any that could be drawn from a rigorous logical sequence of inferences. Indeed, his arguments are simply convincing and persuasive, with little room for doubt. Ideas for theorems seem to come from intuition that follows experience. Experience enough drawings of right triangles inscribed in a circle, and you will discover that the sum of the angles of a triangle is 180°. Experience drawing enough triangles, and you will discover that you can split any triangle into two right triangles. That's the way you would demonstrate a theorem: persuasion by experience. Later, when you are sure that your intuition is right because you have persuasive arguments to show that it is right, you might want to find your theorem's position in the web of others that are ultimately built on self-evident assumptions.
Jesus and I developed an insatiable appetite for mathematics. At the time, I was studying architecture and had no real training in mathematics. The solution to the truck winching problem came to me by accident, without thought. It not only impressed Jesus, but it inspired both of us to consider studying more mathematics. Jesus decided that he would go to university to study engineering.
I started thinking about proof. Pushing the limits of my knowledge at the time, I explained a simple proof of a proposition found in Book I of Euclid's Elements. It says that an isosceles triangle has its base angles equal. Thales proved this proposition sometime back in the fifth century b.c. Later, Pappus, a Greek mathematician who lived around 300 b.c., gave a different proof—a curious proof: Flip the given isosceles triangle around its vertical axis. The triangle is unchanged. Since the angle on the left of the base coincides with the angle on the right, the two base angles must be equal.
If the sides of such an isosceles triangle are extended equal distances beyond the base, the angles under the base will also be equal. This was proven by the same "flip" argument.
In medieval times, this theorem was the end of the road for courses in mathematics. It was known as "the bridge of fools" because the figure looks like the truss of a bridge and also because only a fool couldn't make it across.
This kind of heuristic proof was acceptable in Thales's time, but not in Euclid's. The same proposition appears as Proposition 5 in Book I of Euclid's Elements, with a proof based on far stricter standards. Although heuristics might have played a central role in guiding discovery and acceptance of the theorem, rigor would inevitably challenge any argument not based on strict rules of proof.
I confess that at the time of meeting Jesus, my knowledge of mathematics did not extend beyond this bridge. But later that bridge was moved closer to that wonderful theorem in mathematics called the Pythagorean theorem, which states that the sum of the squares of the lengths of the sides of a right triangle equals the square of the length of the hypotenuse.6 According to the Guinness Book of World Records, the Pythagorean theorem has the most known proofs: 520 different proofs.7
When Jesus heard about Pythagoras's theorem, he tested it on all the triangles he knew, making light sketches of right triangles and measuring sides and hypotenuses. If it looked like it was true for a few triangles, he would not be satisfied until he sketched others and tested the statement again and again on squat, fat, and tall triangles.
How could he have convinced himself of the truth? He would have had to draw some fairly precise right triangles and take reasonably precise measurements of the sides and hypotenuses. Although this method might persuade some people, it wouldn't be enough to convince Jesus, and it certainly wouldn't be enough to convince mathematicians.
However, it doesn't take much evidence to form opinions about mathematical statements. There was good evidence to suggest that the theorem is true. So Roger gave Jesus one of the standard arguments in favor of the truth.
"Draw any right triangle and three squares, one on each side and the third on the hypotenuse," he said.
"You can place the contents of the lower square into the tilted square on the hypotenuse with room to spare. Next, you see that the remaining square on the left will fit into the remaining space of the square on the hypotenuse without room to spare. This should convince you that the sum of the areas of the squares on the sides is equal to the area of the square on the hypotenuse."
"It doesn't convince me," Jesus said.
"Repeat the testing by redrawing right triangles," continued Roger. "You will see that every time you draw a right triangle, no matter how squat or tall, the theorem holds. You should become more accepting, but not entirely persuaded. What you need is some more 'evidence,' not a formal proof in the mathematical sense, but a 'somewhat credible' argument." He sketched several triangles and said, "Examine these triangles and you will become persuaded that the theorem is true."
"I'm not persuaded," I said. "Suppose the triangle has two equal sides. Does it work for such a triangle?" I drew a picture.
Form two squares on the sides of the isosceles right triangle and one square on its hypotenuse.
Divide the smaller squares in half to make four isosceles right triangles.
Fit the triangles into the larger square to fill it exactly.
"Okay, I'm persuaded that it works for the isosceles right triangle," I said. "Now, what others can we be sure of?" I drew a triangle and played with it, but I could not get anywhere.
Frustrated, I began to doodle.
Jesus took one look at my doodling and shouted, "You proved it! All you have to do is rearrange the four triangles in the big square to make the two smaller squares!" And he made the following sketch.
The four shaded triangles can be repositioned from one figure to the other to show that the two squares in the figure on the right must equal the square C in the figure on the left.
It was brilliant. My sketch was nothing more than doodling, yet Jesus saw something I did not. This was by no means a formal proof through a string of logical arguments starting from axioms; nevertheless, it seemed to me to be an airtight argument.
The next day, Jesus told us that he had had a dream that the theorem was not specifically about squares. And when he awoke, he realized that his dream was right.
"It seems that the Pythagorean theorem is about numbers—that is, the squares of the lengths of the sides," Jesus said. "But the square of a length is also the area of a square whose side is that length. So, is the theorem about numbers or geometry?"
"Perhaps it's about both," I said, amazed by the thought and innocent of the remarkable possibility that geometry and arithmetic could reflect each other.
A few days into our trip, we came to the little town of San Mauricio. What a great surprise. The sidewalks on both sides of its short main street were paved in the same mosaic tesseral pattern as those of Caracas. In the center was a bronze statue of Simón Bolivar. The mayor was Jesus's uncle, who spoke English well enough for me to understand him without Roger's help. He was a short man with a bushy moustache, a round face, and curly black hair who constantly chewed tobacco and never removed his sunglasses, even as the evening turned dark. He arranged a feast in our honor. Most of the town was visible from our outdoor feast on a little hill under the shade of tall mahogany trees, with nearby monkeys playfully jumping in all directions. In the distance, I could see long, low buildings that might have been army barracks; three gray water towers; and two rows of thatched roofed mud houses, churuatas. I could see the town communal vegetable garden sprawling down to a wide section of the Manapire River that zigzagged through lush, receding valleys with birds of all colors tunefully sharing fruit and berries of their heavenly habitat.
A magnificently embroidered tablecloth of geometric design was laid out on three long boards supported by tree stumps. Exotic fruits of every kind were placed around the ends to keep the cloth from the welcome evening breezes. Apricots, mangos, and guava were piled high in the center, along with several cooked chickens bathing in thick coconut milk. Two large goldfish bowls of lemonade and cut lemons balanced the boards. My thirst was perpetual, and although I recall the lemonade more vividly than anything else on the table, I still remember the flowers and rainbow-colored berries strategically placed to make an impressive presentation. It was quite a surprise that such a remote village would salute unimportant, uninvited, undeserving strangers with such generous display.
Our host was very interested in America, especially President Kennedy. Conversation was a battle. Although he seemed to be an educated man, he had the charmingly innocent background of someone with only Caracas newspaper and radio versions of the bigger world outside of his remote village.
Jesus, meanwhile, couldn't get enough mathematics. He returned to his thoughts about the Pythagorean theorem and felt that somehow he had to be more convinced. I had no real idea how to prove the theorem in any conventional sense and could only try to persuade him by virtue of experience, intuition, and compelling forces suggesting that it couldn't not be true. Parmenides was referring to this kind of persuasion in his poem The Way of Truth: "The only ways of enquiry that can be thought of: the one way, that it is and cannot not-be, is the path of Persuasion, for it attends upon Truth."
I was amazed to find that even small schoolboys in San Mauricio knew the Pythagorean theorem and could give reasonably persuasive arguments in favor of belief. The mayor called for a boy, no older than ten, to give credible evidence that the theorem is true and to show how well his town's school prepared schoolchildren. The mayor pretended to be choosing a boy at random from a small group of curious children standing at a comfortable distance behind an imaginary dividing line. The boy was dark-skinned, shirtless, and smiling, and had hair combed in an attempt to cover a recent wound to the left side of his head. With a great deal of help from the mayor, the boy allegedly proved the theorem while drawing a picture on the back of an old movie poster of Clark Gable hovering over the exposed cleavage of Janet Leigh.
The schoolboy had given a well-known Hindu "proof" of the Pythagorean theorem. The Hindu version simply gives a picture like the one the boy drew, except that it includes the word BEHOLD! It is a very persuasive picture. From it, you can deduce the Pythagorean theorem by comparing the areas of the triangles, rectangles, and squares in the figure.
The problem with this "Hindu proof" is that it is not really a proof, but merely a picture. The proof is in the ability to rearrange the triangles, rectangles, and squares in such a way that the two small (shaded) squares fit inside the tilted square.
This is essentially what the boy said: "Draw a right triangle. (I). Then draw a square on the hypotenuse (II). You can fit both your triangle and the square on the hypotenuse into a larger square (III). From two corners of the original triangle, draw two lines parallel to the sides (IV), and color or shade the four rectangles defined by the large square and the two lines that you just drew. Your picture should look something like V."
In Figure V, there are four triangles that have the same area as the original triangle. There is a tilted square, which is really the square on the hypotenuse of the original triangle. And there is a big square that borders the entire figure. Next, notice that there are two small squares that are the squares on each of the sides of the original triangle. Let A represent the area of the original triangle. Let B represent the area of the big square.
Check that B – 4A equals the area of the tilted square. Then check that B – 4A also equals the sum of the areas of the squares on the sides of the original triangle. Now use the fact that two things that are equal to a third must be equal to each other to convince yourself that the theorem is true for your original triangle.
The next morning, the mayor, encouraged by the schoolboy's performance, took us to the village school that was established in 1902 and appropriately named, in translation, The Search for Knowledge School. It was impressively active; students were seated at desks working on what appeared to be math projects. The teacher seemed to know the history of mathematics better than mathematics itself, but he was clearly attached to his students. He was a tall man, whiter than his fellow villagers, with a small black beard and a nervous habit of using one hand to pick at the fingernails of the other. He claimed to have spent some time in Texas doing migrant farm work. His English was clear. When I asked about textbooks, he exchanged glances with the mayor and said, "I am the only one with a textbook. We don't have enough textbooks; so I give the lessons from my copy." But the mayor interrupted.
"We have a fine library," he said and immediately led us out of the schoolhouse to proudly lead us to one more place.
 Figure
1.1
Figure
1.1 Figure
1.2
Figure
1.2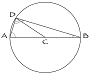 Figure
1.3
Figure
1.3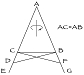 Figure
1.4
Figure
1.4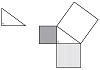 Figure
1.5
Figure
1.5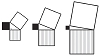 Figure
1.6
Figure
1.6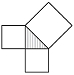 Figure
1.7
Figure
1.7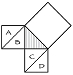 Figure
1.8
Figure
1.8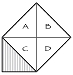 Figure
1.9
Figure
1.9 Figure
1.10
Figure
1.10 Figure
1.11
Figure
1.11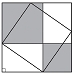 Figure
1.12
Figure
1.12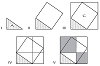 Figure
1.13
Figure
1.13