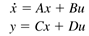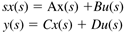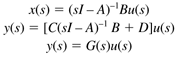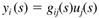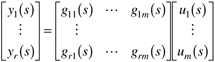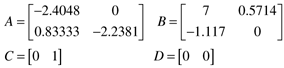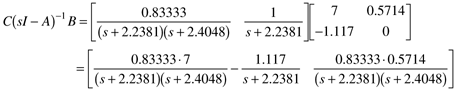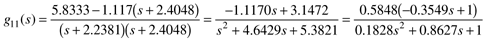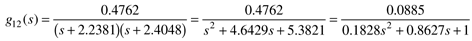- Background
- Linear State Space Models
- Introduction to Laplace Transforms
- Transfer Functions
- First-Order Behavior
- Integrating System
- Second-Order Behavior
- Lead-Lag Behavior
- Poles and Zeros
- Processes with Dead Time
- Padé Approximation for Dead Time
- Converting State Space Models to Transfer Functions
- Matlab and Simulink
- Summary
- References
- Student Exercises
This chapter is from the book
This chapter is from the book
This chapter is from the book
3.12 Converting State Space Models to Transfer Functions
A general state space model can be converted to transfer function form, using the following steps. Starting with the state space model
)
Take the Laplace transform of each term, assuming zero initial conditions
)
Solving for x(s), then y(s) (it should be noted that often D = 0)
)
where G(s) is a transfer function matrix. For example, the transfer function relating input j and output i is
)
or in matrix form (with m inputs and r outputs)
)
Example 3.9: Isothermal CSTR
Consider the isothermal CSTR shown in Example 3.3 and Module 5. The state space model is
)
The first input (u1, manipulated) is the dilution rate (F/V), the second input (u2, disturbance) is the feed concentration (CAf), and the output is the concentration of the intermediate component, B. The eigenvalues of A (obtained by solving det(lI – A) = 0) are –2.4048 and –2.2381 min-1.
The sequence of steps used to find the transfer function matrix is
)
and multiplying,
)
Also,
)
The manipulated input-output process transfer function for the reactor is
)
and the disturbance input-output transfer function is
)
The transfer function poles (–2.2381 and –2.4048) are equal to the eigenvalues of the A matrix. Also, the positive zero (1/0.3549) in g11(s) yields the inverse response shown in Figure 3-5.
){kind=link}
We see that it is straightforward to convert state space models to transfer function models. An n-state system results in transfer functions that have a denominator polynomial that is nth order in s, that is, with n poles. Sometimes the resulting transfer functions can be factored into lower order transfer functions because of pole-zero cancellation (a value of a pole is equal to a value of a zero). An example of pole-zero cancellation is shown in Exercise 13.