- 13.1 Introduction
- 13.2 Experiments
- 13.3 Observation: An Example
- 13.4 Controlling to Block Non-causal Paths
- 13.5 Machine-Learning Estimators
- 13.6 Conclusion
13.3 Observation: An Example
Let’s look at an example of what happens when you don’t make your cause independent of everything else. We’ll use it to show how to build some intuition for how observation is different from intervention. Let’s look at a simple model for the correlation between race, poverty, and crime in a neighborhood. Poverty reduces people’s options in life and makes crime more likely. That makes poverty a cause of crime. Next, neighborhoods have a racial composition that can persist over time, so the neighborhood is a cause of racial composition. The neighborhood also determines some social factors, like culture and education, and so can be a cause of poverty. This gives us the causal diagram in Figure 13.3.
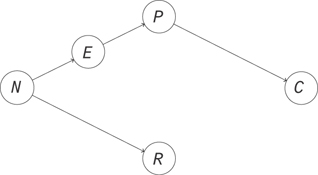
Figure 13.3 The neighborhood is a cause of its racial composition and poverty levels. The poverty level is a cause of crime.
Here, there is no causal relationship between race and crime, but you would find them to be correlated in observational data. Let’s simulate some data to examine this.
1 N = 10000
2
3 neighborhood = np.array(range(N))
4
5 industry = neighborhood % 3
6
7 race = ((neighborhood % 3
8
9 + np.random.binomial(3, p=0.2, size=N))) % 4
10
11 income = np.random.gamma(25, 1000*(industry + 1))
12
13 crime = np.random.gamma(100000. / income, 100, size=N)
14
15 X = pd.DataFrame({'$R$': race, '$I$': income, '$C$': crime,
16
17 '$E$': industry, '$N$': neighborhood})
Here, each data point will be a neighborhood. There are common historic reasons for the racial composition and the dominant industry in each neighborhood. The industry determines the income levels in the neighborhood, and the income level is inversely related with crime rates.
If you plot the correlation matrix for this data (Figure 13.4), you can see that race and crime are correlated, even though there is no causal relationship between them!
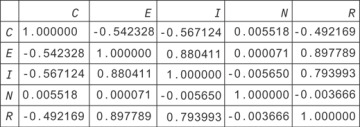
Figure 13.4 Raw data showing correlations between crime (C), industry (E), income (I), neighborhood (N), and race (R)
You can take a regression approach and see how you can interpret the regression coefficients. Since we know the right model to use, we can just do the right regression, which gives the results in Figure 13.5.
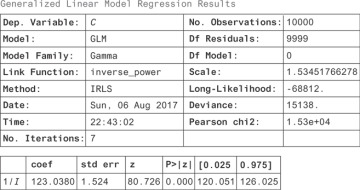
Figure 13.5 Regression for crime against the inverse of income
1 from statsmodels.api import GLM 2 import statsmodels.api as sm 3 4 X['$1/I$'] = 1. / X['$I$'] 5 model = GLM(X['$C$'], X[['$1/I$']], family=sm.families.Gamma()) 6 result = model.fit() 7 result.summary()
From this you can see that when 1/I increases by a unit, the number of crimes increases by 123 units. If the crime units are in crimes per 10,000 people, this means 123 more crimes per 10,000 people.
This is a nice result, but you’d really like to know whether the result is causal. If it is causal, that means you can design a policy intervention to exploit the relationship. That is, you’d like to know if people earned more income, everything else held fixed, would there be less crime? If this were a causal result, you could say that if you make incomes higher (independent of everything else), then you can expect that for each unit decrease in 1/I, you’ll see 123 fewer crimes. What is keeping us from making those claims now?
You’ll see that regression results aren’t necessarily causal; let’s look at the relationship between race and crime. We’ll do another regression as shown here:
1 from statsmodels.api import GLM
2 import statsmodels.api as sm
3
4 races = {0: 'african-american', 1: 'hispanic',
5 2: 'asian', 3: 'white'}
6 X['race'] = X['$R$'] .apply(lambda x: races[x])
7 race_dummies = pd.get_dummies(X['race'])
8 X[race_dummies.columns] = race_dummies
9 model = OLS(X['$C$'], race_dummies)
10 result = model.fit()
11 result.summary()
Figure 13.6 show the result.
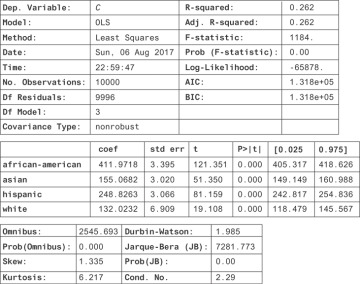
Figure 13.6 Statistics highlighting relationships between race and crime
Here, you find a strong correlative relationship between race and crime, even though there’s no causal relationship. You know that if we moved a lot of white people into a black neighborhood (holding income level constant), you should have no effect on crime. If this regression were causal, then you would. Why do you find a significant regression coefficient even when there’s no causal relationship?
In this example, you went wrong because racial composition and income level were both caused by the history of each neighborhood. This is a case where two variables share a common cause. If you don’t control for that history, then you’ll find a spurious association between the two variables. What you’re seeing is a general rule: when two variables share a common cause, they will be correlated (or, more generally, statistically dependent) even when there’s no causal relationship between them.
Another nice example of this common cause problem is that when lemonade sales are high, crime rates are also high. If you regress crime on lemonade sales, you’d find a significant increase in crimes per unit increase in lemonade sales! Clearly the solution isn’t to crack down on lemonade stands. As it happens, more lemonade is sold on hot days. Crime is also higher on hot days. The weather is a common cause of crime and lemonade sales. We find that the two are correlated even though there is no causal relationship between them.
The solution in the lemonade example is to control for the weather. If you look at all days where it is sunny and 95 degrees Fahrenheit, the effect of the weather on lemonade sales is constant. The effect of weather and crime is also constant in the restricted data set. Any variance in the two must be because of other factors. You’ll find that lemonade sales and crime no longer have a significant correlation in this restricted data set. This problem is usually called confounding, and the way to break confounding is to control for the confounder.
Similarly, if you look only at neighborhoods with a specific history (in this case the relevant variable is the dominant industry), then you’ll break the relationship between race and income and so also the relationship between race and crime.
To reason about this more rigorously, let’s look at Figure 13.3. We can see the source of dependence, where there’s a path from N to R and a path from N through E and P to C. If you were able to break this path by holding a variable fixed, you could disrupt the dependence that flows along it. The result will be different from the usual observational result. You will have changed the dependencies in the graph, so you will have changed the joint distribution of all these variables.
If you intervene to set the income level in an area in a way that is independent of the dominant industry, you’ll break the causal link between the industry and the income, resulting in the graph in Figure 13.7. In this system, you should find that the path that produces dependence between race and crime is broken. The two should be independent.
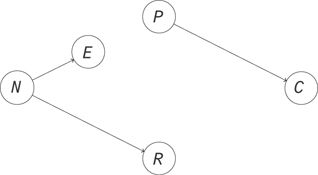
Figure 13.7 The result of an intervention, where you set the income level by direct intervention in a way that is independent of the dominant industry in the neighborhood
How can you do this controlling using only observational data? One way is just to restrict to subsets of the data. You can, for example, look only at industry 0 and see how this last regression looks.
1 X_restricted = X[X['$E$'] == 0]
2
3 races = {0: 'african-american', 1: 'hispanic',
4 2: 'asian', 3: 'white'}
5 X_restricted['race'] = X_restricted['$R$'] .apply(lambda x: races[x])
6 race_dummies = pd.get_dummies(X_restricted['race'])
7 X_restricted[race_dummies.columns] = race_dummies
8 model = OLS(X_restricted['$C$'], race_dummies)
9 result = model.fit()
10 result.summary()
This produces the result in Figure 13.8.
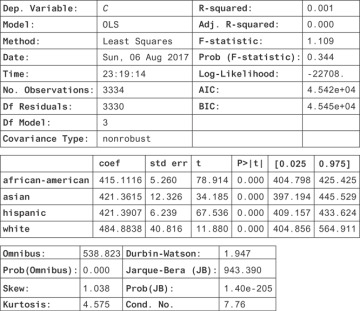
Figure 13.8 A hypothetical regression on race indicator variables predicting crime rates, but controlling for local industry using stratification of the data. There are no differences in expected crimes, controlling for industry.
Now you can see that all of the results are within confidence of each other! The dependence between race and crime is fully explained by the industry in the area. In other words, in this hypothetical data set, crime is independent of race when you know what the dominant industry is in the area. What you have done is the same as the conditioning you did before.
Notice that the confidence intervals on the new coefficients are fairly wide compared to what they were before. This is because you’ve restricted to a small subset of your data. Can you do better, maybe by using more of the data? It turns out there’s a better way to control for something than restricting the data set. You can just regress on the variables you’d like to control for!
1 from statsmodels.api import GLM
2 import statsmodels.api as sm
3
4 races = {0: 'african-american', 1: 'hispanic',
5 2: 'asian', 3: 'white'}
6 X['race'] = X['$R$'] .apply(lambda x: races[x])
7 race_dummies = pd.get_dummies(X['race'])
8 X[race_dummies.columns] = race_dummies
9
10 industries = {i: 'industry_{}' .format(i) for i in range(3)}
11 X['industry'] = X['$E$'] .apply(lambda x: industries[x])
12 industry_dummies = pd.get_dummies(X['industry'])
13 X[industry_dummies.columns] = industry_dummies
14
15 x = list(industry_dummies.columns)[1:] + list(race_dummies.columns)
16
17 model = OLS(X['$C$'], X[x])
18 result = model.fit()
19 result.summary()
Then, you get Figure 13.9 shows the result.
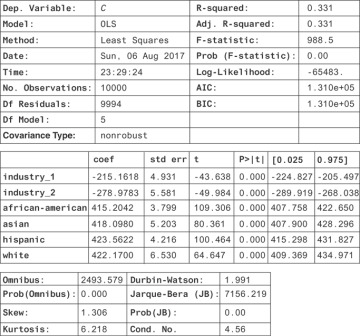
Figure 13.9 Statistics highlighting the relationship between race and industry from an OLS fit
Here, the confidence intervals are much narrower, and you see there’s still no significant association between race and income level: the coeficients are roughly equal. This is a causal regression result: you can now see that there would be no effect of an intervention to change the racial composition of neighborhoods. This simple example is nice because you can see what to control for, and you’ve measured the things you need to control for. How do you know what to control for in general? Will you always be able to do it successfully? It turns out it’s very hard in practice, but sometimes it’s the best you can do.
