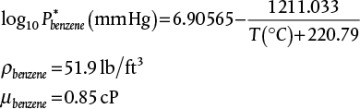Problems
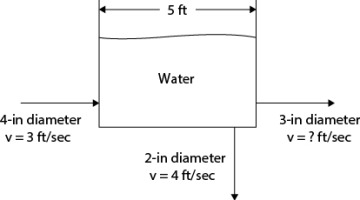
23. Consider the situation depicted in Figure 19.23. The fluid is an oil with a specific gravity of 0.85. Fill in the missing data in Table P19.23.
Figure P19.23
Table P19.23
| Stream | Pipe | 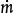 (kg/s) (kg/s) |
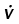 (m3/s) (m3/s) |
u (m/s) |
1 |
2-in, schedule 40 |
6 |
||
2 |
3.5-in, schedule 40 |
0.0106 |
||
3 |
1.5-in, schedule 40 |
4.032 |
||
4 |
3-in, schedule 40 |
24. For water flowing in the situation shown in Figure 19.24 and the data in Table P19.24, do the following:
Calculate the mass flowrate of Stream 3.
Calculate the velocity of Stream 4.
What schedule-40 pipe size must be used in Stream 3?
Figure P19.24
Table P19.24
| Stream | Pipe | u (m/s) |
1 |
1-in, schedule 40 |
5 |
2 |
1.5-in, schedule 40 |
3 |
3 |
?-in, schedule 40 |
2.18 |
4 |
4-in, schedule 40 |
? |
25. Consider the situation depicted in Figure 19.25. The liquid level in the cylindrical tank is increasing at 0.02 ft/sec.
What is the net rate of flow into the tank?
What is the velocity in the 3-in pipe?
26. Water is pumped through a 750-ft length of 6-in, schedule-40 pipe. The discharge at the end of the pipe is 50 ft above the suction end. The pump is 80% efficient and is driven by a 20 hp motor. If the friction loss in the pipe is 50 ft lbf/lb, what is the flowrate through the pipe?
27. A hydroelectric power plant takes 25 m3/s of water from a large reservoir through its turbine and discharges it to the atmosphere at 1 m/s. The turbine is 50 m below the reservoir surface. The frictional head loss in the system is 10 m. The turbine and electric generator as a whole are 80% efficient. Assuming turbulent flow, calculate the power extracted by the turbine.
28. Water is pumped at a constant rate of 10 m3/h from an open tank on the floor to an open tank with a level 10 m above the floor. Frictional losses in the 50-mm-diameter pipe between the tanks are 3.5 J/kg. At what height above the floor must the water level be kept if the pump can develop only 0.1 kW? The pump is 75% efficient.
29. Water in a dam on a 75-ft-deep river is passed through a turbine to produce energy. The outlet of the turbine is 15 ft above the river bed. The mass flowrate of water is 65,000 lb/s, and the inside diameter of the discharge pipe is 10 ft. Discharge is to the atmosphere, and frictional losses may be neglected. For a 55% efficient turbine, calculate the power produced.
30. Many potential drugs have low water solubility, hindering their transport in the body’s aqueous material distribution medium (blood). One way to improve solubility is to decrease particle size below 1 μm diameter. One method to do this is by high-pressure homogenization, using a homogenizer, which is basically a nozzle. In this process, the drug is dispersed in a solvent and forced through a narrow orifice (nozzle) at high pressure. As the liquid enters the orifice, it experiences a pressure drop so great it partially vaporizes. As it exits the constriction, the vapor bubbles collapse violently and produce local disturbances, breaking up the surrounding solid particles.
A high-pressure homogenizer is being used to decrease the size of some drug particles. The particles are suspended in water at 25°C and sent through the homogenizer at 250 mL/min. The pressure before the orifice is 34.5 MPa, and the diameter of the pipe is 0.1 m. Determine the diameter orifice (nozzle) that results in an exit pressure at the vapor pressure of water. Neglect friction.
31. A pump operating at 80% efficiency delivers 30 gal/min of water from a reservoir to an open-air storage tank at a chemical plant 1 mi away. A 3-in, schedule-40 pipe is used, and the frictional losses are 200 ft lbf/lb. The elevation of the liquid level in the tank is 873 ft above sea level, and the elevation of the liquid level in the reservoir is 928 ft above sea level.
What is the minimum horsepower required for the pump?
The elevation of the reservoir is fixed. What elevation of the liquid level of the tank would make the pump unnecessary?
32. A pressurized tank situated above ground level contains a liquid with specific gravity of 0.9. The liquid flows down to ground level through 4-in, schedule-40 pipe through a pump (75% efficiency) and into a tank at a level 25 m above the level of the source tank at a pressure of 550 kPa through 2-in, schedule-40 pipe. The pump power is 6.71 kW. A pressure gauge at the pump entrance reads 115.6 kPa, and a pressure gauge at the pump discharge reads 762.6 kPa. The frictional losses in the piping on the suction side of the pump and on the discharge side of the pump are 30 J/kg and 50 J/kg, respectively.
What is the mass flowrate of liquid through the system?
What is the velocity in the 2-in, schedule-40 pipe?
What is the pressure of the liquid in the source tank?
Determine whether the kinetic energy contribution to the mechanical energy balance is small.
33. Water is pumped from one storage tank to a higher tank at a steady rate of 10-3m3/s. The difference in the elevations of the two water tanks is 50 m. The storage tank, which serves a source, is open to the atmosphere, while the tank receiving the water has a pressure of 170.3 kPa. Pressure gauges in the pipeline at the inlet and outlet of the pump read 34.5 kPa and 551.6 kPa, respectively. The power supplied by an electric motor to the pump shaft is 1000 W. All piping is 1-in, schedule-40 steel pipe. Find the pump efficiency and friction loss in the pipe per kg of water.
34. Oil (SG = 0.88) flows at 5 ft3/s from one tank, through a pump, to another tank. The pipe diameter between the source tank and the pump is 12 in, and the pipe diameter between the pump and the destination tank is 6 in. The liquid level in the source tank is 10 ft above the pump, which is at ground level. The liquid level in the destination tank is 12 ft. The source tank is at 25 psia, and the destination tank is open to the atmosphere. A manometer is connected to the upstream and downstream pipes, immediately adjacent to the pump, with a differential height of 36 in of mercury. The pump is 75% efficient. Frictional losses may be neglected.
What is the power rating of the pump?
What is the maximum possible height of the bottom of the destination tank?
35. A fluid with specific gravity of 0.8 is in a tank, at a pressure of 150 kPa, with a level maintained at 5 m above ground level. The fluid leaves the tank through 4-in, schedule-40 pipe (frictional loss of 30 J/kg) at a mass flowrate of 6.5 kg/s and enters a pump at ground level. The pump power is 1.5 kW and is 70% efficient. The fluid leaving the pump flows through 3.5-in, schedule-40 pipe (frictional loss of 50 J/kg) to a “final” point in the pipe above the original tank level, where the pressure is 200 kPa.
Find the velocity at the final point in the pipe.
Determine the pressure at the pump inlet.
Determine the height above the ground of the final point in the pipe.
36. Consider the problem of how long it takes for a tank to drain. Consider an open-top cylindrical tank with one horizontal exit pipe at the bottom of the tank that discharges to the atmosphere. The tank has a diameter, d, and the height of liquid in the tank at any time is h.
The mass balance is unsteady state. Explain why the mass balance is
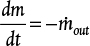
where m is the mass of liquid in the tank and
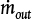 is the mass flowrate out of the tank.
is the mass flowrate out of the tank.The mass in the tank is the fluid density times the volume of liquid in the tank. The flowrate,
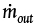 , can be related to the velocity and the cross-sectional area of the exit pipe based on what we have already learned. The volume of liquid in the tank can be related to the height of liquid in the tank. Simplify the differential mass balance to obtain an expression for the height of liquid in the tank as a function of the velocity of the liquid through the exit pipe.
, can be related to the velocity and the cross-sectional area of the exit pipe based on what we have already learned. The volume of liquid in the tank can be related to the height of liquid in the tank. Simplify the differential mass balance to obtain an expression for the height of liquid in the tank as a function of the velocity of the liquid through the exit pipe.Now, write a mechanical energy balance on the fluid in the tank and pipe from the top level in the tank to the pipe outlet, neglecting friction. It is generally assumed the velocity of the tank level (i.e., the fluid level in the tank) is small because of the large diameter. Solve for the velocity, and rearrange the differential equation to look like
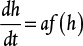
where a is a group of constants and f(h) is a function of the height that you have derived.
Solve this differential equation for height as a function of time with the initial condition of a height of ho at time zero.
Rearrange the answer to Part (d) to get an expression for the time for complete drainage.
37. The following equations describe a fluid-flow system. Draw and label the system.
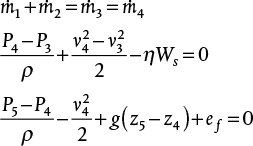
38. The following equations describe a fluid flow system, with friction neglected. Draw and label the system, making sure that your diagram is visually accurate.
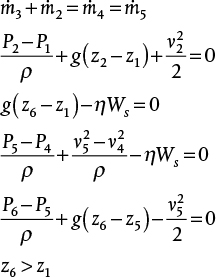
39. An aneurysm is a weakening of the walls of an artery causing a ballooning of the arterial wall. The result is a region of larger diameter than a normal artery. If the “balloon” ruptures in a high-blood-flow area, such as the aorta, death is almost instantaneous. Fortunately, there are often symptoms due to slow leakage that can precede rupture. What happens to the blood velocity as it passes through the aneurysm? Justify your answer using equations. In the human body, very small changes in pressure can be significant. Using the mechanical energy balance, neglecting only friction and potential energy effects, analyze the pressure change as blood enters the aneurysm a large distance from the heart, so that the pulse flow is not an issue. The blood is flowing in a region not in the vicinity of the heart. What is the effect of the observed pressure change?
40. A pipeline is replaced by new 2-in, schedule-40, commercial-steel pipe. What power would be required to pump water at a rate of 100 gpm through 6000 ft of this pipe?
41. Hot water at 43°C flows from a constant-level tank through 2-in, schedule-40, commercial-steel pipe, from which it emerges 12.2 m below the level in the tank. The equivalent length of the piping system is 45.1 m. Calculate the rate of flow in m3/s.
42. Crude oil (μ = 40 cP, SG = 0.87) is to be pumped from a storage tank to a refinery through a series of pump stations via 10-in, schedule-20, commercial-steel pipeline at a flowrate of 2000 gpm. The pipeline is 50 mi long and contains 35 90° elbows and 10 open gate valves. The pipeline exit is 150 ft higher than the entrance, and the exit pressure is 25 psig. What horsepower is required to drive the pumps if they are 70% efficient?
43. A pipeline to carry 1 million bbl/day of crude oil (1 bbl = 42 gal, SG = 0.9, μ = 25 cP) is constructed with 50-in-inside-diameter, commercial-steel pipe and is 700 mi long. The source and destination are at atmospheric pressure and the same elevation. There are 50 wide-open gate valves, 25 half-open globe valves, and 50 45° elbows. There will be 25 identical pumps along this pipeline, each with an efficiency of 70%. What is the power required for each pump?
44. A pump draws a solution of specific gravity 1.2 with the viscosity of water from a ground-level storage tank at 50 psia through 3.5-in, schedule-40, commercial-steel pipe at a rate of 12 lb/s. The pump produces 4.5 hp with an efficiency of 75%. The pump discharges through a 2.5-in, schedule-40 commercial steel pipe to an overhead tank at 100 psia, which is 50 ft above the level of solution in the feed tank. The suction line has an equivalent length of 20 ft, including the tank exit. The discharge line contains a half-open globe valve, two wide-open gate valves, and two 90° elbows. What is the maximum total length of discharge piping allowed for this pump to work?
45. Many chemical plants store fuel oil in a “tank farm” on the outskirts of the plant. To prevent an environmental disaster, there are specific rules regarding the design of such facilities. One such rule is that there be an emergency dump tank with the capacity of the largest storage tank. Should a leak or structural problem occur with a tank, the fuel oil can be pumped into the emergency dump tank.
Consider the design of the pumping system from a 250 m3 tank storing #6 fuel oil into a 250 m3 dump tank. The viscosity of #6 fuel oil is 0.8 kg/m s, and its density is 999.5 kg/m3. The piping system consists of 43 m of commercial-steel pipe, four 90° flanged regular elbows, a sharp entrance, an exit, and a pump. The oil must be pumped to an elevation 3.35 m above the exit point from the source tank.
If 20-in, schedule-40, commercial-steel pipe is used, and if it is necessary to accomplish the transfer within 45 min, determine the power rating required of the pump. Assume the pump is 80% efficient.
If the pump to be used has 10 kW at 80% efficiency, and the pipe is 20-in, schedule-40, commercial-steel pipe, determine how long the transfer will take.
If the pump to be used has 20 kW at 80% efficiency, and the transfer is to be accomplished in 45 min, determine the required schedule-40 pipe size.
46. Two parallel sections of pipe branch from the same split point. Both branches end at the same pressure and the same elevation. Branch 1 is 3-in, schedule-40, commercial-steel pipe and has an equivalent length of 12 m. Branch 2 is 2-in, schedule-80, commercial-steel pipe and has an equivalent length of 9 m.
Assuming fully turbulent flow, what is the split ratio between the two branches?
Suppose that Branch 2 ends 5 m higher than Branch 1. What is the split ratio between the branches in this case?
47. Consider a two-pipes-in-series system: that is, Pipe 1 is followed by Pipe 2. The liquid is water at room temperature with a mass flowrate of 2 kg/s. The pipes are horizontal. Calculate the pressure drop across these two pipes and the power necessary to overcome the frictional loss. Ignore the minor losses due to the pipe fitting. The pipe data are
Pipe |
L (m) |
Pipe Size |
Material |
1 |
10 |
1-in, schedule-40 |
Commercial steel |
2 |
15 |
2-in, schedule-40 |
Cast iron |
48. Assume that the same two pipes in Problem 19.47 are now in parallel with the same total pressure drop. Compute the mass flowrate in each section of pipe. Neglect additional frictional losses due to the parallel piping. Explain the reason for the observed split between the parallel pipes.
49. A pipe system to pump #6 fuel oil (μ = 0.8 kg/m s, ρ = 999.5 kg/m3) consists of 50 m of 8-in, schedule-40, commercial-steel pipe. It has been observed that the pressure drop is 8.79 × 104 Pa.
Determine the volumetric flowrate of the fuel oil.
Extra capacity is needed. Therefore, it has been decided to add a parallel line of the same length (neglect minor losses) using 5-in, schedule-40, commercial-steel pipe. By what factor will the fuel oil volumetric flowrate increase?
50. There are three equal-length sections of identical 3-in, schedule-40, commercial-steel pipe in series. An increased flowrate of 20% is needed. How is the pressure drop affected? It is decided to replace the second section with two equal-length, identical sections of the original pipe in parallel. How is the pressure drop in this system affected relative to the original case? Neglect minor losses due to elbows and fittings and assume fully developed turbulent flow.
51. Consider two parallel arteries of the same length, both fed by a main artery. The flowrate in the main artery is 10-6 m3/s. One branch is stenotic (has plaque build-up due to too many Big Macs, Double Whoppers, etc.). The stenotic artery will be modeled as a rigid pipe with 60% the diameter of the healthy artery (diameter of 0.1 cm). For this problem, blood may be considered to be a Newtonian fluid with the properties of water. What fraction of the blood flows in each arterial branch? Be sure to validate any assumptions made.
52. One of the potential benefits of the production of shale gas is that certain seams of the gas contain significant amounts of ethane, which can be cracked into ethylene, a building block for many other common chemicals (polyethylene, ethylene oxide, which is made into ethylene glycol among many others, and tetrafluoroethylene, the monomer for Teflon). Assume that a cracker plant produces ethylene (C2H4) at 5 atm and 70°F. It is to be delivered by pipeline to a neighboring plant, which was built near the ethylene cracker facility, which is 10 miles away. The pressure at the neighboring plant entrance must be 2.5 atm. It has been suggested that 6-in, schedule-40, commercial-steel pipe be used. What delivery mass flowrate is possible with this pipe size? If you need to make an assumption, do so and prove its validity.
53. Natural gas (methane, μ = 10-5 kg/m s) must flow in a pipeline between compression stations. The compressor inlet pressure is 250 kPa, and its outlet pressure is 1000 kPa. Assume isothermal flow at 25°C. The pipe is 6-in, schedule-40, commercial steel. The mass flowrate is 2 kg/s. What is the required distance between pumping stations?
54. Your plant produces ethylene at 6 atm and 60°F. It is to be delivered to a neighboring plant 5 miles away via pipeline, and the pressure at the neighboring plant entrance must be 2 atm. The contracted delivery flowrate is 2 lb/sec. It has been suggested that 4-in, schedule-40, commercial-steel pipe be used. Evaluate this suggestion. Be sure to validate any assumptions made.
55. Calculate the terminal velocity of a 2 mm diameter lead sphere (SG = 11.3) dropped in air. The properties of air are ρ = 1.22 kg/m3 and μ = 1.81 × 10-5 kg/m s.
56. A packed bed is composed of crushed rock with a density of 200 lb/ft3 with an assumed particle diameter of 0.15 in. The bed is 8 ft deep, has a porosity of 0.3, and is covered by a 3 ft layer of water that drains by gravity through the bed. Calculate the velocity of water through the bed, assuming the water enters and exits at 1 atm pressure.
57. A hollow steel sphere, 5 mm in diameter with a mass of 0.05 g, is released in a column of liquid and attains an upward terminal velocity of 0.005 m/s. The liquid density is 900 kg/m3, and the sphere is far enough from the container walls so that their effect may be neglected. Determine the viscosity of the liquid in kg/m s. Hint: Assume Stokes flow and confirm the assumption with your answer.
58. In a particular sedimentation vessel, small particles (SG = 1.1) are settling in water at 25°C. The particles have a diameter of 0.1 mm. What is the terminal velocity of the particles? Validate any assumptions made.
59. At West Virginia University, each Halloween, there is a pumpkin-drop contest. College, high-school, and middle-school students participate. The goal is to drop a pumpkin off the top of the main engineering building (assume about 100 ft) and have it land close to a target without being damaged. Packing and parachutes are commonly used. You have a theory that the terminal velocity at which a pumpkin packed in your newly invented, proprietary bubble wrap can hit the ground and remain intact is 50 m/s. You will use no parachute, and the shape will be approximately spherical. The pumpkin plus wrapping has a diameter of 40 cm. By calculating the actual terminal velocity, determine whether the pumpkin will exceed the desired terminal velocity. Assume that the wrapped pumpkin has the specific gravity of water, and assume the air is at 25°C and 1 atm.
60. Air enters and passes up through a packed bed of solids 1 m in height. Using the data provided, what are the pressure drop and the outlet pressure?
Data:
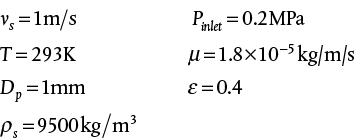
61. In the regeneration of a packed bed of ion-exchange resin, hydrochloric acid (SG = 1.2, μ = 0.002 kg/m s) flows upward through a bed of resin particles (particle density of 2500 kg/m3). The bed is 40 cm in diameter, and the particles are spherical with a diameter of 2 mm and a bed void fraction of 0.4. The bed is 2 m deep, and the bottom of the bed is 2 m off the ground. The acid is pumped at a rate of 2 ×10-5 m3/s from an atmospheric pressure, ground-level storage tank through the packed bed and into another atmospheric pressure, ground-level storage tank, in which the filled height is 2 m. The complete piping system consists of 75 equivalent meters of 4-in, schedule-40, commercial-steel pipe.
Determine the required power of a 75% efficient pump for this duty. Remember that a pump must be sized for the maximum duty needed.
What do you learn from the numbers in Part (a) regarding the relative magnitudes of the maximum duty and the steady-state duty?
What is the pressure rise needed for the pump?
62. A gravity filter is made from a bed of granular particles assumed to be spherical. The bed porosity is 0.40. The bed has a diameter of 0.3 m and is 1.75 m deep. The volumetric flowrate of water at 25°C through the bed is 0.006 m3/s. What particle diameter is required to obtain this flowrate?
63. Calculate the flowrate of air at standard conditions required to fluidize a bed of sand (SG = 2.4) if the air exits the bed at 1 atm and 70°F. The sand grains have an equivalent diameter of 300 μm, and the bed is 3 ft in diameter and 1.5 ft deep, with a porosity of 0.33.
64. Consider a catalyst, specific gravity 1.75, in a bed with air flowing upward through it at 650 K and an average pressure of 1.8 atm (μair = 3 × 10-5 kg/m s). The catalyst is spherical with a diameter of 0.175 mm. The static void fraction is 0.55, and the void fraction at minimum fluidization is 0.56. The slumped bed height is 3.0 m, and the fluidized bed height is 3.1 m.
Calculate the minimum fluidization velocity.
Calculate the pressure drop at minimum fluidization.
Estimate the pressure drop at one-half of the minimum fluidization velocity assuming incompressible flow.
65. A manometer containing oil with a specific gravity (SG) of 1.28 is connected across an orifice plate in a horizontal pipeline carrying seawater (SG = 1.1). If the manometer reading is 16.8 cm, what is the pressure drop across the orifice? What is it in inches of water?
66. Water is flowing downhill in a pipe that is inclined 35° to the horizontal. A mercury manometer is attached to pressure taps 3 in apart. The interface in the downstream manometer leg is 1.25 in higher than the interface in the upstream leg. What is the pressure drop between the two pressure taps?
67. An orifice having a diameter of 1 in is used to measure the flowrate of SAE 10 lube oil (SG = 0.928, μ = 60 cP) in a 2.5-in, schedule-40, commercial-steel pipe at 70°F. The pressure drop across the orifice is measured by a mercury (SG = 13.6) manometer, which reads 3 cm.
Calculate the volumetric flowrate of the oil.
How much power is required to pump the oil through the orifice (not the pipe, just the orifice)?
68. You must install a centrifugal pump to transfer a volatile liquid from a remote tank to a point in the plant 1000 ft from the tank. To minimize the distance that the power line to the pump must be strung, it is desirable to locate the pump as close as possible to the plant. If the liquid has a vapor pressure of 30 psia, the pressure in the tank is 30 psia, the level in the tank is 40 ft above the pump inlet, and the required pump NPSH is 20 ft, what is the closest that the pump can be located to the plant without the possibility of cavitation? The line is 2-in, schedule-40, commercial steel, the flowrate is 75 gpm, and the fluid properties are ρ = 45 lb/ft3 and μ = 5 cP.
69. Refer to Figure 19.69. Answer the following questions. Explain each answer.
At what flowrate is NPSHA = 3.2 m? Comment on the feasibility of operating at this flowrate.
At what flowrate does the pump produce 33.5 m of head? What is the system frictional loss at this flowrate? What is the pressure drop across the control valve at this flowrate?
At what flowrate does cavitation become a problem?
What is the maximum possible flowrate?
If the source and destination pressures are identical, what is the elevation difference between source and destination?
At a flowrate of 1 L/s, what is the system frictional head loss?
At a flowrate of 1 L/s, what head is developed by the pump?
At a flowrate of 1 L/s, what is the head loss across the control valve?
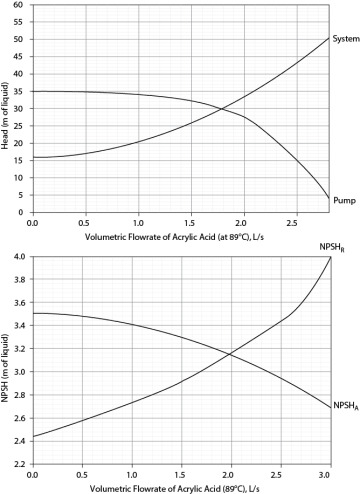
Figure P19.69 Volumetric Flowrate of Acrylic Acid (at 89°C), L/s
70. Benzene at atmospheric pressure and 41°C is in a tank with a fluid level of 15 ft above a pump. The pump provides a pressure increase of 50 psi to a destination 25 ft above the tank fluid level. The suction line to the pump has a length of 20 ft and is 2-in, schedule-40. The discharge line has a length of 40 ft to the destination and is 1.5-in, schedule-40. The flowrate of benzene is 9.9 lb/sec.
Derive an expression for the NPSH in head units (ft of liquid) vs. flowrate in ft3/s.
Derive an expression for the system curve in head units (ft of liquid) vs. flowrate in ft3/s.
Locate the operating point on both plots on Figure 19.70.
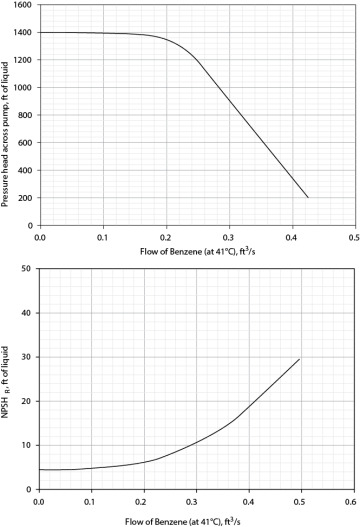
Figure P19.70 Flow of Benzene (at 41°C), ft3/s
What is the maximum flowrate before cavitation becomes a problem?
What is the pressure drop across the valve at the operating point?
What is the maximum flowrate possible with one pump, two pumps in series, and two pumps in parallel?
Data:
71. Acrylic acid at 89°C and 0.16 kPa (ρ = 970 kg/m3, μ = 0.46 cP) leaves the bottom of a distillation column at a rate of 1.5 L/s. The bottom of a distillation column may be assumed to behave like a tank containing vapor and liquid in equilibrium at the temperature and pressure of the exit stream. The liquid must be pumped to a railroad heading supply tank 4.0 m above the liquid level in the distillation column, where the pressure must be 116 kPa. The liquid level at the bottom of the distillation column is 3.5 m above the pump suction line, and the frictional head loss for the suction line including the tank exit is 0.2 m of acrylic acid. There is a cooler after the pump with a pressure drop of 3.5 m of acrylic acid. The discharge line is 1.5-in, schedule-40, commercial-steel pipe, with an equivalent length of 200 m. The entire process may be assumed to be isothermal at 89°C. The problem at hand is whether this system can be scaled up by 20%. The plots required for this analysis are in Figure 19.71.
Based on a pump/system curve analysis, can this portion of the process be scaled up by 20%? If not, what is the maximum scale-up percentage?
Based on an NPSH analysis, is it good operating policy for this portion of the process to be scaled up by 20%? If not, what is the maximum recommended scale-up percentage?
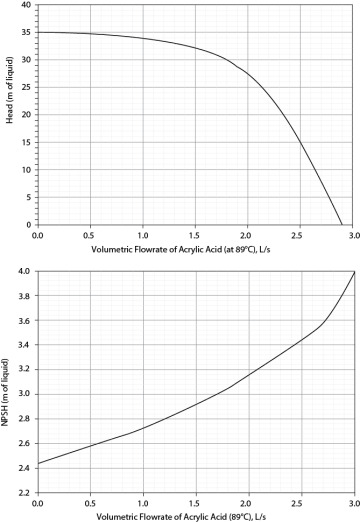
Figure P19.71 Volumetric Flowrate of Acrylic Acid (89°C), L/s
72. Consider the pump and system curves indicated by the data in Table P19.72. Answer the following questions.
If the source and destination are at the same height, what is the pressure change from source to destination?
The operating condition is 1.2 L/s. What is ΔPfriction at this point?
At 1.2 L/s, what pressure change does the pump provide?
At 1.2 L/s, what is the pressure drop across the control valve following the pump?
What is the maximum flowrate possible with this (assumed single) pump?
What is the maximum flowrate possible with two identical pumps in series?
What is the maximum flowrate possible with two identical pumps in parallel?
Table P19.72
| Pump Curve | System Curve | ||
| Pressure Developed (kPa) | Flowrate (L/s) | Pressure Change (kPa) | Flowrate (L/s) |
225.0 |
0.00 |
54.0 |
0.00 |
225.0 |
0.40 |
59.0 |
0.50 |
225.0 |
0.80 |
80.0 |
1.00 |
224.0 |
1.20 |
115.0 |
1.50 |
220.0 |
1.50 |
200.0 |
2.00 |
185.0 |
1.86 |
559.0 |
2.50 |
0.0 |
2.60 |
||