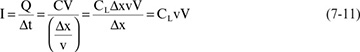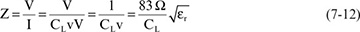- 7.1 Forget the Word Ground
- 7.2 The Signal
- 7.3 Uniform Transmission Lines
- 7.4 The Speed of Electrons in Copper
- 7.5 The Speed of a Signal in a Transmission Line
- 7.6 Spatial Extent of the Leading Edge
- 7.7 “Be the Signal”
- 7.8 The Instantaneous Impedance of a Transmission Line
- 7.9 Characteristic Impedance and Controlled Impedance
- 7.10 Famous Characteristic Impedances
- 7.11 The Impedance of a Transmission Line
- 7.12 Driving a Transmission Line
- 7.13 Return Paths
- 7.14 When Return Paths Switch Reference Planes
- 7.15 A First-Order Model of a Transmission Line
- 7.16 Calculating Characteristic Impedance with Approximations
- 7.17 Calculating the Characteristic Impedance with a 2D Field Solver
- 7.18 An n-Section Lumped-Circuit Model
- 7.19 Frequency Variation of the Characteristic Impedance
- 7.20 The Bottom Line
- End-of-Chapter Review Questions
7.8 The Instantaneous Impedance of a Transmission Line
We can quantify our analysis so far in this chapter by building a simple physical model of the transmission line. We can model the line as an array of little capacitor buckets, each one equal to the capacitance in the transmission line that spans a footstep and separated by the distance we, the signal, move in each footstep. We call this model (the simplest model we can come up with that provides engineering insight) the zeroth-order model of a transmission line (see Figure 7-9). It is a physics model and not an equivalent circuit model. Circuit models do not have lengths in them.
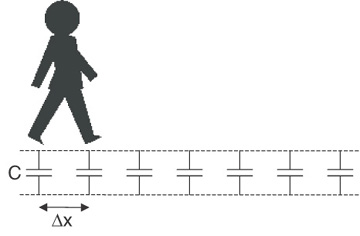
Figure 7-9 Zeroth-order model of a transmission line composed of an array of capacitors. With each footstep, another capacitor is charged up. The spacing is the size of our footstep.
In this model, the size of each footstep is Δx. The magnitude of each little capacitor bucket is the capacitance per length, CL, of the line times the length of each footstep:
We can calculate the current out of our foot, I, using this model. The current is the charge that flows out of our foot to charge up each bucket in the time interval between each step. The charge we dump in each capacitor bucket, Q, is the capacitance of the bucket times the voltage applied, V. For each step we take, we are dumping the charge Q into the line, in a time interval of a step.
The time between steps, Δt, is the length of our step, Δx, divided by our speed down the line, v. Of course, as the real signal propagates, each footstep is really small, but the time interval between steps gets really small as well. The ratio of the charge that flows to each time interval is a constant value, which is the current that flows into the line as the signal propagates:
where:
I = current from the signal
Q = charge in each footstep
C = capacitance of each footstep
Δt = time to step from capacitor to capacitor
CL = capacitance per length of the transmission line
Δx = distance between the capacitors or each footstep
v = speed of walking down the line
V = voltage of the signal
This says the current coming out of our foot and going into the line is simply related to the capacitance per length, the speed of propagation, and the voltage of the signal—exactly as we reasoned earlier.
This is the defining relationship for the current-voltage (I-V) behavior of a transmission line. It says the instantaneous current of a signal anywhere on a transmission line is directly proportional to the voltage. Double the voltage applied, and the current into the transmission line will double. This is exactly how a resistor behaves. With each step down the transmission line, the signal sees an instantaneous impedance that behaves like a resistive load.
From this relationship, we can calculate the instantaneous impedance a signal would see at each step as it propagates down a transmission line. The instantaneous impedance is the ratio of the voltage applied to the current through the device:
where:
Z = instantaneous impedance of the transmission line, in Ohms
CL = capacitance per length of the line, in pF/inch
v = speed of light in the material
εr = dielectric constant of the material
The instantaneous impedance a signal sees depends on only two terms, both of which are intrinsic to the line. It doesn’t depend on the length of the line. The instantaneous impedance of the line depends on the cross section of the line and the material properties. As long as these two terms are constant as we move down the line, a signal would see the same constant, instantaneous impedance. And, of course, the units we use to measure the instantaneous impedance of the line are Ohms, as with any impedance.
Since the speed of the signal depends on a material property, we can relate the capacitance per length of the transmission line to the instantaneous impedance. For example, if the dielectric constant is 4 and the capacitance per length of the line is 3.3 pF/inch, the instantaneous impedance of the transmission line is:
What about the inductance of the line? Where does that come into play in this model? The answer is that this zeroth-order model is not an electrical model; it is a physical model. Rather than approximating the transmission line with Ls and Cs, we added the observation that the speed of the signal is the speed of light in the material.
In reality, the finite speed of the signal arises partly because of the series loop inductance per length of the signal and return paths. If we used a first-order, equivalent circuit model, including the inductance per length, it would derive for us the current into the transmission line and the finite propagation speed, but the model would be more complicated mathematically.
These two models are really equivalent, considering the connection between the propagation speed and the inductance per length. As we shall see, the propagation delay is directly related to the capacitance per length combined with the inductance per length. The speed of the signal has in it some assumptions about the inductance of the conductors.