- 7.1 Forget the Word Ground
- 7.2 The Signal
- 7.3 Uniform Transmission Lines
- 7.4 The Speed of Electrons in Copper
- 7.5 The Speed of a Signal in a Transmission Line
- 7.6 Spatial Extent of the Leading Edge
- 7.7 “Be the Signal”
- 7.8 The Instantaneous Impedance of a Transmission Line
- 7.9 Characteristic Impedance and Controlled Impedance
- 7.10 Famous Characteristic Impedances
- 7.11 The Impedance of a Transmission Line
- 7.12 Driving a Transmission Line
- 7.13 Return Paths
- 7.14 When Return Paths Switch Reference Planes
- 7.15 A First-Order Model of a Transmission Line
- 7.16 Calculating Characteristic Impedance with Approximations
- 7.17 Calculating the Characteristic Impedance with a 2D Field Solver
- 7.18 An n-Section Lumped-Circuit Model
- 7.19 Frequency Variation of the Characteristic Impedance
- 7.20 The Bottom Line
- End-of-Chapter Review Questions
7.7 “Be the Signal”
All a signal cares about is how fast it moves down the line and what impedance it sees. As we saw previously, speed is based on the material properties of the dielectric and their distribution. To evaluate the impedance a signal sees in propagating down the line, we will take a microstrip transmission line and launch a signal into one end. A microstrip is a uniform but unbalanced transmission line. It has a narrow-width signal line and a wide return path.
The analysis we will do of this line is identical to that for any transmission line. We’ll make it 10 feet long, so that we can actually walk down it and, in a Zen way, “be the signal” to observe what the signal would see. With each step along the way, we will ask What impedance do we see? We will answer this question by determining the ratio of the voltage applied, 1 v, and the current coming out of our foot to drive the signal down the transmission line.
In this case, we launch a signal into one end by connecting a 1-v battery between the two conductors at the front end. At the initial instant that we have launched the signal into the line, there has not been enough time for the signal to travel very far down the line.
Just to make it easier, let’s assume that we have air between the signal and return paths, so the speed of propagation is 1 foot per nsec. After the first nsec, the voltage on the far end of the line is still zero, as the signal hasn’t had enough time to get very far. The signal along the line would be about 1 volt for the first foot and zero for the remaining length of the line.
Let’s freeze time after the first nsec and look at the charges on the line. What we see is illustrated in Figure 7-8. Between the signal- and return-path conductors in the first 12 inches, there will be a 1-volt difference. This is, after all, the signal. We know that because the signal and return paths are two separated conductors, there will be some capacitance between the conductors in this region. If there is a 1-v difference between them, there must also be some charge on the signal conductor and an equal and opposite amount on the return-path conductor.
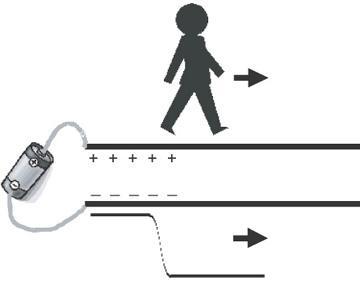
Figure 7-8 Charge distribution on the transmission line after a 1-v signal has propagated for 1 nsec. There is no charge ahead of us (the signal) at this instant in time.
In the next 1 nsec, we, being the signal, will move ahead another 12 inches. Let’s stop time again. We now have the first 2 feet of line charged up. We see that having made this last step, we have brought the signal to the second foot-long section and created a voltage difference between the signal and return conductors. There is now a charge difference between the two conductors, at the point of each footstep, where there was none a nsec ago.
As we walk down the line, we are bringing a voltage difference to the two conductors and charging them up. In each nsec, we take another 1-foot step and charge up this new section of the line. Each step of the signal will leave another foot of charged transmission line in our wake.
The charge that flowed to charge up each footstep came from the signal, as each foot came down, and ultimately from the battery. The fact that the signal is propagating down the line means that the capacitance between the signal and return paths is getting charged up. How much charge has to flow from our foot into the line in each footstep? In other words, what is the current that must flow to charge up successive regions of the transmission line as the signal propagates?
If the signal is moving down the line at a steady speed and the line is uniform—that is, it has the same capacitance per length—then we are injecting the same amount of charge into the line with each footstep. Each step charges up the same amount of capacitance to the same voltage. If we are always taking the same time per step, then we are injecting the same charge per unit of time for the signal to charge up the line. The same amount of charge per nsec flowing into the line means that there is a constant current flowing into the line from our foot.
What affects the current coming out of our foot to charge up the line? If we are moving down the line at a constant speed, and if we increase the width of the signal path, the capacitance we need to charge up will increase, and the charge that must come out of our foot in the time we have till the next step will increase. Likewise, if anything is done to decrease the capacitance per length of the interconnect, the current coming out of our foot to charge up the reduced capacitance will decrease. For the same reason, if the capacitance per length stays the same, but our speed increases, we will be charging up more length per nsec, and the current needed will increase.
In this way, we can deduce that the current coming out of our foot will scale directly with both the capacitance per length and the speed of the signal. If either increases, the current out of our foot with each step will increase. If either decreases, the current from the signal to charge up the line will decrease. We have deduced a simple relationship between the current coming out of our foot and the properties of the line:
where:
I = current out of our foot
v = speed with which we move down the line, charging up regions
CL = capacitance per length of the line
As we, the signal, move down the transmission line, we will constantly be asking What is the impedance of the line? The basic definition of impedance of any element is the ratio of voltage applied to current through it. So, as we move down the line, we will constantly be asking with each footstep What is the ratio of the voltage applied to the current being injected into the line?
The voltage of the signal is fixed at the signal voltage. The current into the line depends on the capacitance of each footstep and how long it takes to charge up each footstep. As long as the speed of the signal is constant and the capacitance of each footstep is constant, the current injected into the line by our foot will be constant, and the impedance of the line the signal sees will be constant.
We call the impedance the signal sees with each step the instantaneous impedance. If the interconnect features are uniform, the instantaneous impedance will be the same for each footstep. A uniform transmission line is called a controlled impedance transmission line because the instantaneous impedance is controlled to be the same everywhere on the line.
Suppose the line width were to suddenly widen. The capacitance of each footstep would be larger, and the current coming out of each footstep to charge up this capacitance would be larger. A higher current for the same voltage means we see the transmission line having a lower impedance in this region. The instantaneous impedance is lower in this part of the transmission line.
Likewise, if the line were to suddenly narrow, the capacitance of each footstep would be less, the current required to charge it up would be less, and the instantaneous impedance the signal would see for the line would be higher.
The instantaneous impedance depends on the speed of the signal, which is a material property, and the capacitance per length. For a uniform transmission line, the cross-sectional geometry is constant down the line, and the instantaneous impedance the signal sees will be constant down the line. As we will see, an important behavior of a signal interacting with a transmission line is that whenever the signal sees a change in the instantaneous impedance, some of the signal will reflect and some will continue distorted. In addition, signal integrity may be affected. This is the primary reason controlling the instantaneous impedance the signal sees is so important.


