- 7.1 Forget the Word Ground
- 7.2 The Signal
- 7.3 Uniform Transmission Lines
- 7.4 The Speed of Electrons in Copper
- 7.5 The Speed of a Signal in a Transmission Line
- 7.6 Spatial Extent of the Leading Edge
- 7.7 “Be the Signal”
- 7.8 The Instantaneous Impedance of a Transmission Line
- 7.9 Characteristic Impedance and Controlled Impedance
- 7.10 Famous Characteristic Impedances
- 7.11 The Impedance of a Transmission Line
- 7.12 Driving a Transmission Line
- 7.13 Return Paths
- 7.14 When Return Paths Switch Reference Planes
- 7.15 A First-Order Model of a Transmission Line
- 7.16 Calculating Characteristic Impedance with Approximations
- 7.17 Calculating the Characteristic Impedance with a 2D Field Solver
- 7.18 An n-Section Lumped-Circuit Model
- 7.19 Frequency Variation of the Characteristic Impedance
- 7.20 The Bottom Line
- End-of-Chapter Review Questions
7.5 The Speed of a Signal in a Transmission Line
If the speed of the electrons isn’t what determines the speed of the signal, what does?
Figure 7-6 illustrates the simplest way to think of a signal propagating down a transmission line. The signal, after all, is a propagating voltage difference between the signal path and the return path. As the signal propagates, a voltage difference must be created between the two conductors. Accompanying the voltage difference is an electric field between the conductors.
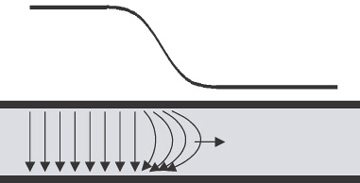
Figure 7-6 The electric field building up in a transmission line as the signal propagates down the line. The speed of the signal depends on how fast the changing electric and magnetic fields can build up and propagate in the materials surrounding the signal- and return-path conductors.
In addition to the voltage, a current must be flowing in the signal conductor and in the return conductor to provide the charge that charges up the conductors that generates the voltage difference that creates the electric field. This current loop moving through the conductors will produce a magnetic field.
A signal can be launched into a transmission line simply by touching the leads of a battery to the signal and return paths. The sudden voltage change creates a sudden electric and magnetic-field change. This kink of field will propagate through the dielectric material surrounding the transmission line at the speed of a changing electric and magnetic field, which is the speed of light in the material.
We usually think of light as the electromagnetic radiation we can see. However, all changing electromagnetic fields are exactly the same and are described by exactly the same set of equations, Maxwell’s Equations. The only difference is the frequency of the waves. For visible light, the frequency is about 1,000,000 GHz. For the signals typically found in high-speed digital products, the frequency is about 1–10 GHz.
How quickly the electric and magnetic fields can build up is what really determines the speed of the signal. The propagation and interaction of these fields is described by Maxwell’s Equations, which say that if the electric and magnetic fields ever change, the kink they make will propagate outward at a speed that depends on some constants and material properties.
The speed of the change, or the kink, v, is given by:
where:
ε0 = permittivity of free space = 8.89 × 10−12 F/m
εr = relative dielectric constant of the material
μ0 = permeability of free space = 4π × 10–7 H/m
μr = relative permeability of the material
Putting in the numbers, we find:
For virtually all interconnect materials, the magnetic permeability of the dielectrics, μr, is 1. All polymers that do not contain a ferromagnetic material have a magnetic permeability of 1. Therefore, this term can be ignored.
In comparison, the relative dielectric constant of materials, εr, is never less than or equal to 1, except in the case of air. In all real interconnect materials, the dielectric constant is greater than 1. This means the speed of light in interconnects will always be less than 12 inches/nsec. The speed is:
For brevity, we usually refer to the relative dielectric constant as just the “dielectric constant.” This number characterizes some of the electrical properties of an insulator. It is an important electrical property. For most polymers, it is roughly 4. For glass, it is about 6, and for ceramics, it is about 10.
It is possible in some materials for the dielectric constant to vary with frequency. In other words, the speed of light in a material may be frequency dependent. We call this property dispersion, a frequency dependence to the speed of light in the material. In general, dielectric constant decreases with higher frequency. This makes the speed of light in the material increase as we go toward higher frequency. In most applications, dispersion is very small and can be ignored.
In most common materials, such as FR4, the dielectric constant varies very little from 500 MHz to 10 GHz. Depending on the ratio of epoxy resin to fiberglass, the dielectric constant of FR4 can be from 3.5 to 4.5. Most interconnect laminate materials have a dielectric constant of about 4. This suggests a simple, easy-to-remember generalization.
As pointed out in Chapter 5, “The Physical Basis of Capacitance,” when the field lines see a combination of dielectric materials, as in a microstrip where there are some field lines in the bulk material and some in the air above, the effective dielectric constant that affects the signal speed is a combination of the different materials. The only way to predict the effective dielectric constant when the materials are inhomogeneous throughout the cross section is with a 2D field solver. In the case of stripline, for example, all the fields see the same material, and the effective dielectric constant is the bulk dielectric constant.
The time delay, TD, and length of an interconnect are related by:
where:
TD = time delay, in nsec
Len = interconnect length, in inches
v = speed of the signal, in inches/nsec
This means that to travel down a 6-inch length of interconnect in FR4, for example, the time delay is about 6 inches/6 inches/nsec, or about 1 nsec. To travel 12 inches takes about 2 nsec.
The wiring delay, the number of psec of delay per inch of interconnect, is also a useful metric. It is just the inverse of the velocity: 1/v. For FR4, the wiring delay is about 1/6 inches/nsec = 0.166 nsec/inch, or 170 psec/inch. This is the delay per inch of a signal propagating down a transmission line in FR4. Every inch of interconnect has a propagation delay of 170 psec. The total delay through the 0.5 inch of a BGA lead is 170 psec/inch × 0.5 inches = 85 psec.




