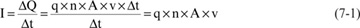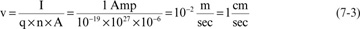- 7.1 Forget the Word Ground
- 7.2 The Signal
- 7.3 Uniform Transmission Lines
- 7.4 The Speed of Electrons in Copper
- 7.5 The Speed of a Signal in a Transmission Line
- 7.6 Spatial Extent of the Leading Edge
- 7.7 “Be the Signal”
- 7.8 The Instantaneous Impedance of a Transmission Line
- 7.9 Characteristic Impedance and Controlled Impedance
- 7.10 Famous Characteristic Impedances
- 7.11 The Impedance of a Transmission Line
- 7.12 Driving a Transmission Line
- 7.13 Return Paths
- 7.14 When Return Paths Switch Reference Planes
- 7.15 A First-Order Model of a Transmission Line
- 7.16 Calculating Characteristic Impedance with Approximations
- 7.17 Calculating the Characteristic Impedance with a 2D Field Solver
- 7.18 An n-Section Lumped-Circuit Model
- 7.19 Frequency Variation of the Characteristic Impedance
- 7.20 The Bottom Line
- End-of-Chapter Review Questions
7.4 The Speed of Electrons in Copper
How fast do signals travel down a transmission line? If it is often erroneously believed that the speed of a signal down a transmission line depends on the speed of the electrons in the wire. With this false intuition, we might imagine that reducing the resistance of the interconnect will increase the speed of a signal. In fact, the speed of the electrons in a typical copper wire is actually about 10 billion times slower than the speed of the signal.
It is easy to estimate the speed of an electron in a copper wire. Suppose we have a roughly 18-gauge round wire, 1 mm in diameter, with 1 Amp of current. We can calculate the speed of the electrons in the wire based on how many electrons pass by one section of the wire per second, the density of the electrons in the wire, and the cross-sectional area of the wire. This is illustrated in Figure 7-5. The current in the wire is related to:
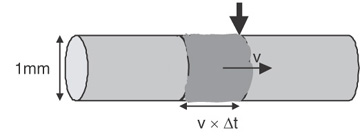
Figure 7-5 The electrons moving down a wire. The number passing the arrow per second is the current and is related to the velocity and number density of the electrons.
from which we can calculate the velocity of the electrons as:
where:
I = current passing one point, in Amps
ΔQ = charge flowing in a time interval, in Coulombs
Δt = time interval
q = charge of one electron = 1.6 × 10−19 Coulombs
n = density of free electrons, in #/m3
A = cross-sectional area of the wire, in m2
v = speed of the electrons in the wire, in m/sec
Each copper atom contributes roughly two free electrons that can move through the wire. Atoms of copper are about 1 nm apart. This makes the density of free electrons, n, about n ∼ 1027/m3.
For a wire that is 1 mm in diameter, the cross-sectional area is about A ∼ 10–6 m2. Combining these terms and using a 1-Amp current in the wire, the speed of an electron in the wire can be estimated to be roughly:
With this simple analysis, we see that the speed of an electron in a wire is incredibly slow compared to the speed of light in air. The speed of an electron in a wire really has virtually nothing to do with the speed of a signal. Likewise, as we will see, the resistance of the wire has only a very small, almost irrelevant effect on the speed of a signal in a transmission line. It is only in extreme cases that the resistance of an interconnect affects the signal speed—and even then the effect is only very slight. We must recalibrate our intuition from the erroneous notion that lower resistance will mean faster signals.
But how do we reconcile the speed of a signal with the incredibly slow speed of the electrons in a wire? How does the signal get from one end of the wire to the other in a much shorter amount of time than it takes an electron to get from one end to the other? The answer lies in the interactions between the electrons.
If we have a pipe filled with marbles and push one marble in on one end, another marble comes out the other end almost instantaneously. The interaction between marbles—the force of one marble on the next one—is transmitted from marble to marble much faster than the actual speed of the marbles.
When a train is stopped at a crossing and starts up again, the couplings between the cars engage down the train much faster than the locomotive inches forward. In the same way, when one electron in a wire is jiggled by the source, its interaction with the adjacent electron through the electric field between them jiggles. This kink in the electric field propagates to the next electron at the speed of light allowed by the changing field.
When an electron on one end of the wire moves, the kink in the electric field propagates to the next electron, and that electron moves, creating a kink in its electric field to the next electron, and all the way down the chain until the last electron moves out the wire at the other end. It’s the speed of the interactions—the kinks in the electric field between the electrons—that determines how fast this signal propagates, not the speed of the electrons themselves.