- 7.1 Forget the Word Ground
- 7.2 The Signal
- 7.3 Uniform Transmission Lines
- 7.4 The Speed of Electrons in Copper
- 7.5 The Speed of a Signal in a Transmission Line
- 7.6 Spatial Extent of the Leading Edge
- 7.7 “Be the Signal”
- 7.8 The Instantaneous Impedance of a Transmission Line
- 7.9 Characteristic Impedance and Controlled Impedance
- 7.10 Famous Characteristic Impedances
- 7.11 The Impedance of a Transmission Line
- 7.12 Driving a Transmission Line
- 7.13 Return Paths
- 7.14 When Return Paths Switch Reference Planes
- 7.15 A First-Order Model of a Transmission Line
- 7.16 Calculating Characteristic Impedance with Approximations
- 7.17 Calculating the Characteristic Impedance with a 2D Field Solver
- 7.18 An n-Section Lumped-Circuit Model
- 7.19 Frequency Variation of the Characteristic Impedance
- 7.20 The Bottom Line
- End-of-Chapter Review Questions
This chapter is from the book
This chapter is from the book
This chapter is from the book
7.19 Frequency Variation of the Characteristic Impedance
So far, we have been assuming that the characteristic impedance of a transmission line is constant with frequency. As we have seen, the input impedance, looking into the front of a transmission line, is strongly frequency dependent. After all, at low frequency, the input impedance of a transmission line open at the far end looks like a capacitor, and the impedance starts high and drops very low.
Does the characteristic impedance vary with frequency? In this section, we are assuming that the transmission line is lossless. In Chapter 9, we will look at the case where the transmission line has loss. We will see that the characteristic impedance does vary slightly due to the losses.
As we have seen, the characteristic impedance of an ideal lossless transmission line is related to the capacitance and inductance per length as:
)
Provided that the dielectric constant of the interconnect is constant with frequency, the capacitance per length will be constant. This is a reasonable assumption for most materials, though in some cases, the dielectric constant will vary slightly.
As we saw in Chapter 6, “The Physical Basis of Inductance,” the loop inductance per length of a line will vary with frequency due to skin-depth effects. In fact, the loop inductance will start out higher at low frequency and decrease as all the currents distribute to the outer surface. This would suggest that characteristic impedance will start out higher at low frequency and decrease to a constant value at higher frequency.
At frequencies well above the skin depth, we would expect all the currents to be on the outer surface of all the conductors and not to vary with frequency beyond this point. The loop inductance should be constant, and the characteristic impedance should be constant. We can estimate this frequency for a 1-ounce copper conductor. The skin depth for copper is about 20 microns at 10 MHz. The thickness of 1-ounce copper is about 34 microns. We would expect to see the characteristic impedance start to decrease around 1 MHz to 10 MHz and stop decreasing at about 100 MHz, where the skin depth is only 6 microns.
We can calculate the frequency dependence of the characteristic impedance for a 50-Ohm microstrip with 1-ounce copper traces by using a 2D field solver. The result is shown in Figure 7-43. At low frequency, the characteristic impedance is high, it starts dropping at about 1 MHz, and it continues to drop until about 50 MHz. The total drop from DC to high frequency is about 7 Ohms, or less than 15%.
)
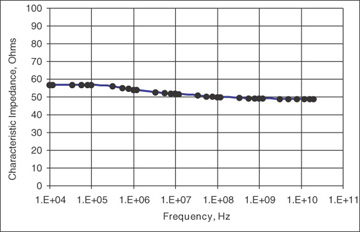
Figure 7-43 Calculated frequency variation of the characteristic impedance due to skin-depth effects, for a 50-Ohm line in FR4 with 1-ounce copper traces. Calculated with Ansoft’s 2D Extractor.