- 7.1 Forget the Word Ground
- 7.2 The Signal
- 7.3 Uniform Transmission Lines
- 7.4 The Speed of Electrons in Copper
- 7.5 The Speed of a Signal in a Transmission Line
- 7.6 Spatial Extent of the Leading Edge
- 7.7 “Be the Signal”
- 7.8 The Instantaneous Impedance of a Transmission Line
- 7.9 Characteristic Impedance and Controlled Impedance
- 7.10 Famous Characteristic Impedances
- 7.11 The Impedance of a Transmission Line
- 7.12 Driving a Transmission Line
- 7.13 Return Paths
- 7.14 When Return Paths Switch Reference Planes
- 7.15 A First-Order Model of a Transmission Line
- 7.16 Calculating Characteristic Impedance with Approximations
- 7.17 Calculating the Characteristic Impedance with a 2D Field Solver
- 7.18 An n-Section Lumped-Circuit Model
- 7.19 Frequency Variation of the Characteristic Impedance
- 7.20 The Bottom Line
- End-of-Chapter Review Questions
7.13 Return Paths
In the beginning of this chapter, we emphasized that the second trace is not the ground but the return path. We should always remember that all current, without exception, travels in loops.
Where is the current loop in a signal propagating on a transmission line? Suppose we have a microstrip that is very long. In this first case, we’ll make it so long that the one-way time delay, TD, is 1 second. This is about the distance from the earth to the moon. To make it easier to think about for now, we will short the far end. We launch a signal into the line. This is shown in Figure 7-18. We have said in this chapter that this means we have a constant current going into the signal path, related to the voltage applied and the characteristic impedance of the line.
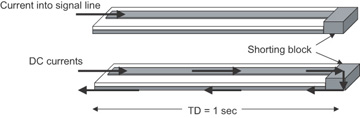
Figure 7-18 Current injected into the signal path of a transmission line and the current distribution after a long time. When does the current actually exit the return path?
If current travels in loops and must return to the source, eventually we’d expect to see the current travel to the end of the line and flow back down the return path. But how long does this take? The current flow in a transmission line is very subtle. When do we see the current come out the return path? Does it take 2 seconds—1 second to go down and 1 second to come back? What would happen then if the far end were really open? If there is insulating dielectric material between the signal and return conductors, how could the current possibly get from the signal to the return conductor, except at the far end?
The best way of thinking about it is by going back to the zeroth-order model, which describes the line as a bunch of tiny capacitors. This is shown in Figure 7-19. Consider the current flow initially. As the signal launches into the line, it sees the first capacitor. As we described in Chapter 5, “The Physical Basis of Capacitance,” if the voltage across the initial capacitor is constant, there will be no current flow through this capacitor. The only way current flows through a capacitor is if the voltage across it changes. As the signal is launched into the transmission line, the voltage across the signal- and return-path conductors ramps up. It is during this transition time, as the edge passes by, that the voltage is changing and current flows through the initial capacitor. As current flows into the signal path to charge up the capacitor, exactly the same amount of current flows out of the return path, having gone through the capacitor.
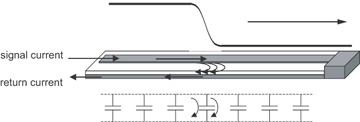
Figure 7-19 Signal current gets to the return path through the distributed capacitance of the transmission line. Current is flowing only from the signal conductor to the return conductor where the signal voltage is changing—where there is a dV/dt.
In the first picosecond, the signal has not gotten very far down the line, and it has no idea how the rest of the line is configured, whether it is open, shorted, or whether it has some radically different impedance. The current flow back to the source, through the return path, depends only on the immediate environment and the region of the line where the voltage is changing—that is, where the signal edge is.
The current from the source flows into the signal conductor and, through displacement current, passes through the capacitance between the signal and return path, and back out the return path. This is the current loop. As the voltage transition edge propagates down the line, this current loop wavefront propagates down the transmission line, flowing between the signal and return path by displacement current.
We can extend the transmission line model to include the rest of the signal and return paths with all the various distributed capacitors between them. As the signal propagates down the line, there is current—the return current—flowing through the capacitance to the return-path conductor and looping back to the source. However, this displacement current loop from the signal path to the return path, flows between them only where the signal voltage is changing.
A few nsec after the signal launch, near the front end, the signal edge has passed by and the voltage is constant, and there is no current flow between the signal to the return path. There is just constant current flowing into the signal conductor and back out the return conductor. Likewise, in front of the signal edge, before the edge has gotten to that region of the line, the voltage is constant, and there is no current flow between the signal and return paths. It is only at the signal edge that current flows through the distributed capacitance.
Once the signal is launched into the line, it will propagate down the line as a wavefront, at the speed of light. Current will flow down the signal line, pass through the capacitance of the line, and travel back through the return path as a loop. The front of this current loop propagates outward coincident with the voltage edge. We see that the signal is not only the voltage wave front, but it is also the current loop wavefront, which is propagating down the line. The instantaneous impedance the signal sees is the ratio of the signal voltage to the signal current.
Anything that disturbs the current loop will disturb the signal and cause a distortion in the impedance, compromising signal integrity. To maintain good signal integrity, it is important to control both the current wave front and the voltage wave front. The most important way of doing this is to keep the impedance the signal sees constant.
When the return path is a plane, it is appropriate to ask where the return current flows? What is its distribution in the plane? The precise distribution is slightly frequency dependent and is not easy to calculate with pencil and paper. This is where a good 2D field solver comes in handy.
An example of the current distribution in a microstrip and a stripline for 10-MHz and 100-MHz sine waves of current is shown in Figure 7-20. We can see two important features. First, the signal current is only along the outer edge of the signal trace. This is due to skin depth. Second, the current distribution in the return path is concentrated in the vicinity of the signal line. The higher the sine-wave frequency, the closer to the surface this current distribution will be.
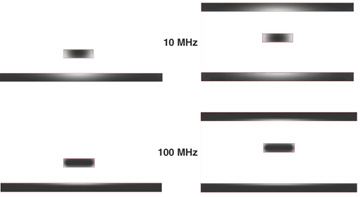
Figure 7-20 Current distribution in the signal and return paths for a microstrip and a stripline at 10 MHz and 100 MHz. In both cases, the line width is 5 mils, and it is 1-ounce copper. Lighter color indicates higher current density. Results calculated with Ansoft’s 2D Extractor.
As the frequency increases, the current in the signal and return path will take the path of lowest impedance. This translates into the path of lowest loop inductance, which means the return current will move as close to the signal current as possible. The higher the frequency, the greater the tendency for the return current to flow directly under the signal current. Even at 10 MHz, the return current is highly localized.
In general, for frequencies above about 100 kHz, most of the return current flows directly under the signal trace. Even if the trace snakes around a curvy path or makes a right-angle bend, the return current in the plane follows it. By taking this path, the loop inductance of the signal and return will be kept to a minimum.
We see that the way to engineer the return path is to control the signal path. Routing the signal path around the board will also route the return current path around the board. This is a very important principle of circuit board routing.

