- 1.1 What Is Mass Transfer?
- 1.2 Preliminaries: Continuum and Concentration
- 1.3 Flux Vector
- 1.4 Concentration Jump at Interface
- 1.5 Application Examples
- 1.6 Basic Methodology of Model Development
- 1.7 Conservation Principle
- 1.8 Differential Models
- 1.9 Macroscopic Scale
- 1.10 Mesoscopic or Cross-Section Averaged Models
- 1.11 Compartmental Models
- Summary
- Review Questions
- Problems
1.9 Macroscopic Scale
At the macro-level of modeling, a large-size control volume or the whole equipment is used. The conservation laws are, in turn, applied to this region. The volume element is not taken to tend toward zero, and the balances based on the selected larger volume are used directly. Such models are useful to obtain the relation between engineering quantities in an approximate way. Point-to-point information (details) is lost at this level, however, and the effects of these variations have to be incorporated through some sort of calculation (model averaging followed by some approximations) or by other means (e.g., empirical fitting of experimental data). This leads to the information loss principle:
Information, on length (or time) scales lower than that at which analysis is done, is lost and has to be supplemented in some suitable manner.
Appreciation and awareness of this principle are important in modeling. In particular, for the macroscale analysis discussed in this section, we lose information on the point-to-point concentration values and the point-wise variation of the flux over a given control surface. This loss must be countered by making some assumptions and using some closure models. In the following sections we discuss qualitatively the closures commonly used by examining some specific examples. More fully worked-out examples of macroscopic balances are provided in Chapter 3 and continued in Chapter 13.
1.9.1 Stirred Tank Reactor: Mixing Model
Consider a reactor that is stirred and operated continuously with in and out flows of a liquid. The control volume is the whole reactor shown in Figure 1.10; the various contributions to the mass conservation are also shown in a general manner in this figure. Now assume the reactor consists of a single phase and is operating at steady state. The accumulation term is zero. The loss term for the second phase shown in the figure can also be neglected here if we have only one phase. The conservation law simplifies to
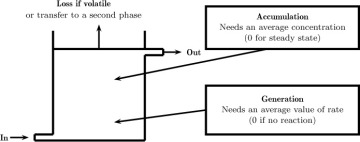
Figure 1.10 Illustration of a macroscopic control volume showing the various components that go into the species balance. The average values are the integrals of the (unresolved) pointwise values. The information on the pointwise values is lost at the macro-scale modeling level. Hence model assumptions or closures are needed.
in – out + generation = 0
where all the terms are in moles A per unit time.
Now let’s use mathematical terms to describe this system. In and out can be formulated in terms of the volumetric flow rate times the corresponding concentration. The main assumption needed is for the generation term. This term is the total generation over the entire control volume and is the volume integral of the local rate of reaction (mole/m3 local volume sec) RA. The local rate, in turn, is a function of the local concentration. We assume that the required relation is known from a kinetic model. Now the generation over the entire volume is the volume integral of the local rate:
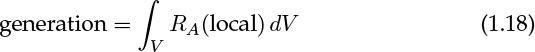
Here RA (local) is some specified function of the local or pointwise concentration.
This local concentration is not known (not being modeled) in the macroscopic model, so it is not possible to evaluate precisely the generation term. Hence some assumption about the mixing level in the reactor (the concentration variation in the reactor) must be made. These details are studied in Chapters 3 and 13.
A common simplifying assumption is that the reactor is well mixed and the reactants present at a uniform concentration. This permits us to close the model, which is then referred to as a completely backmixed model. Many other models for closure may be used depending on the anticipated mixing level in the system (e.g., dividing the tank into a mixed zone and a dead zone or dividing the tank into two well-mixed subcompartments), and some of these models are explained in more detail in Chapter 13. The main point to note here is that some assumption about the mixing pattern must be made and the level of mixing needs to be tested and quantified by suitable experiments (e.g., by tracer methods).
1.9.2 Sublimation of a Solid Sphere: Mass Transfer Coefficient
Consider a solid that exerts sufficient vapor pressure and is subliming into a gas phase. The change in the radius of the solid is to be computed. A macroscopic balance for the solid is in order. In is zero and out is the mass transferred from solid to gas. In this scenario, the conservation law for the solid simplifies to
in (zero) – out (transferred from solid to gas) = accumulation
The rate of transfer from solid to gas is precisely the surface integral of the radially directed outward flux at the surface of the solid:
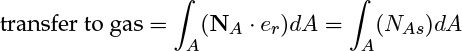
where NAs is the radial component of the flux vector at the surface.
This flux vector can be computed only if a differential model for the gas phase is solved, including the convection and diffusion of the solute in the gas phase. It is not always possible to do this (or such details may not be important) since this endeavor is computationally intensive and the velocity profile in the gas phase may not be precisely known for complex geometries and for turbulent flow. Obviously, we need a closure for the unknown term, which done by introducing the mass transfer coefficient, km. Using this parameter, we model the transfer rate as a product of the mass transfer coefficient times a concentration difference:

CAs – CAb is taken as a driving force for mass transfer from the solid to the bulk gas. Note that CAs is the concentration of A in the gas phase at the gas side of the solid–gas interface, just near the solid. CAb is the concentration in the gas phase at a point far away from the solid, known as the bulk gas. This concentration is usually taken as zero.
Equation 1.19 is actually a definition, rather than a fundamental law. The mass transfer rate is given per unit area of transfer. Balancing the unit, we find that the mass transfer coefficient has the units of m/s. Values of the mass transfer coefficient are provided by numerous sources. For example, they may be empirically fit to experimental data or fit to detailed computational models. For many practical cases the values of the coefficient have previously been published; as a consequence, the concept of the mass transfer coefficient is widely used in practical design calculations. The main point here is that the use of the mass transfer coefficient completes the missing flux information in the context of macro-level (as well as meso-level) models.
1.9.3 Model for Mixer-Settler
Consider the mixer-settler shown in Figure 1.5. There are two phases present in this system: the dispersed phase (drops) and the continuous phase. Obviously, the differential model for both the dispersed and continuous phases is needed for a detailed analysis and can be quite challenging to construct. Here a two-phase flow model together with a local model for interfacial flux needs to be developed. In industrial design, however, macroscopic models are usually the models of choice. Here we assume that there are two control volumes: one for the solvent phase and one for the aqueous phase. These two control volumes have a common interface across which the solute is transferred. In other words, the system is modeled as two interconncected control volumes, one for the aqueous phase and one for the solvent phase. A schematic of such control volumes used in macroscopic analysis of two-phase systems is shown in Figure 1.11. The transfer rate is modeled by using a suitably defined mass transfer coefficient. In addition, we must make an assumption about the mixing pattern in both phases as well as the value for the mass transfer coefficient. For example, are these phases completely mixed? In that case the backmixed assumption is sufficient. Also, how does the mass transfer coefficient change if some design parameter (e.g., agitation speed) is changed? These details needed to design the equipment are explored in more depth in Chapters 3 and 13. At this stage, the various components needed for a macroscale analysis and design of separation equipment simply need to be appreciated.
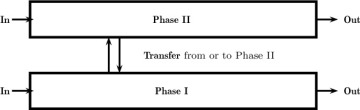
Figure 1.11 Schematic of a mixer-settler for liquid–liquid extraction modeled as two separate but interconnected control volumes.
1.9.4 Equilibrium Stage Model
A simplifying assumption in the mixer-settler model is that the outlet streams are at equilibrium. This will be the case for an ideal contactor in which the mass transfer is complete. Such a simplified model, which is called equilibrium stage model, provides a benchmark for quick design calculations. The actual contactor may not have achieved equilibrium, so the results are often simply corrected by introducing a stage efficiency parameter. This can be an empirically fitted parameter, or it can be computed by including mass transfer effects into the model. Thus we note that a hierarchy of models with increasing levels of complexity can be built for this process—a practice that is common when modeling other separation processes as well. For example, a distillation column can be modeled using (1) a number of ideal or theoretical stages, (2) a number of stages with correction for stage efficiency, or (3) a model based on detailed mass transfer rates.
We now look at mesoscopic models.
