- 1.1 What Is Mass Transfer?
- 1.2 Preliminaries: Continuum and Concentration
- 1.3 Flux Vector
- 1.4 Concentration Jump at Interface
- 1.5 Application Examples
- 1.6 Basic Methodology of Model Development
- 1.7 Conservation Principle
- 1.8 Differential Models
- 1.9 Macroscopic Scale
- 1.10 Mesoscopic or Cross-Section Averaged Models
- 1.11 Compartmental Models
- Summary
- Review Questions
- Problems
This chapter is from the book
This chapter is from the book
This chapter is from the book
1.4 Concentration Jump at Interface
Another important point to understand is that the concentration is not continuous at a phase boundary (e.g., gas–liquid interface), unlike temperature. Consider air–water system as an example. Is the oxygen concentration on the air side of the interface the same as the oxygen concentration on the water side of the gas–liquid interface? The answer is no. Because oxygen has a poor solubility in water, the oxygen concentration in the water phase in much lower than that in the air phase. This difference in concentration is called the concentration jump at the interface. The thermodynamic relations needed to calculate the jump are for various cases are discussed next.
1.4.1 Gas–Liquid Interface: Henry’s Law
The concentrations on the gas side and on the liquid side of the interface are often assumed to be linearly proportional—a concept summarized by Henry’s law. The constant of proportionality is known as the Henry’s law constant. Various definitions are used for this constant, depending on the units used to measure the concentrations. The common form is as follows:
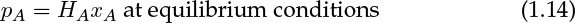
where pA is the partial pressure of the species in the gas phase and xA is the mole fraction in the liquid. The constant HA has the units of atm or Pa or bars here. The values of the Henry’s law constant for some common gases are shown in Table 1.2.
Table 1.2 Henry’s Law Constant for Some Common Gaseous Species in Water at 298.15 K
Gas |
H, atm |
Hydrogen |
7.099 × 104 |
Oxygen |
4.259 × 104 |
Nitrogen |
8.65 × 104 |
Ozone |
4570 |
Carbon dioxide |
1630 |
Sulfur dioxide |
440 |
Ammonia |
30 |
The larger the value of the Henry’s law constant, HA, the less soluble the gas is in the liquid phase. The effect of total pressure in the system is to increase the solubility in accordance with Henry’s law. In general, increasing the temperature decreases the solubility. Hence the Henry’s law constant is usually an increasing function of temperature. An exception occurs with hydrogen, which shows a retrograde behavior. Here the solubility increases at first with an increase in temperature, reaches a maximum, and then decreases thereafter.
Other Definitions of Henry’s Law Constant
Other definitions of the Henry’s law constant are also used, depending on which unit is used for the concentrations in the two phases. Two common definitions are as follows:
where HA,pc is the Henry’s law constant (unit of Pa m3/mol) with partial pressure, Pa, as the unit for the gas phase and mol/m3 as the concentration unit for the liquid phase, respectively. Another form is
where HA,cp is the Henry’s law constant (unit of mol/Pa m3) and is the reciprocal of HA,pc.
Since the concentration in the gas phase can also be used instead of the partial pressure unit, we have yet more ways of writing the Henry’s law relationship! Example 1.1 shows the application of the Henry’s law and the concentration jump at a gas–liquid interface.
Note: Mass transport is usually performed under non-equilibrium conditions. Hence Henry’s law should be applied only at the interface, which is assumed to still be at equilibrium. Concentrations in phase 1 and phase 2, away from the interface, will not be the equilbrium values. Otherwise, no mass transfer will occur.
The schematic of the concentration variation for interfacial mass transfer is shown in Figure 1.3. Although the concentration varies in both phases, the interfacial concentration values are related by thermodynamic considerations. The subscript i in Figure 1.3 refers to the interface and yAi and xAi are related by Henry’s law.
)
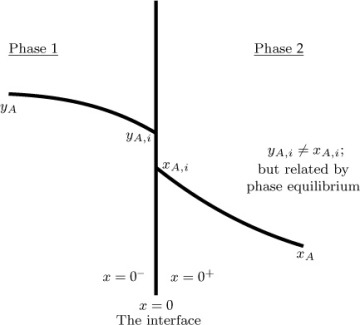
Figure 1.3 Schematic of the concentration jump at an interface.
1.4.2 Vapor–Liquid Interface: Raoult’s Law
For volatile liquid-phase species, Raoult’s law is often used to relate the interfacial concentrations. It states that at the vapor–liquid interface, a pure liquid exerts a partial pressure equal to the vapor pressure of the liquid at that temperature. For an ideal liquid mixture, the partial pressure at the interface is equal to the vapor pressure multiplied by the mole fraction in the liquid. Hence the interfacial relation is
pA,i = xA,i pvap,A
The vapor pressure pvap varies as a function of temperature and is often correlated by the Antoine equation:
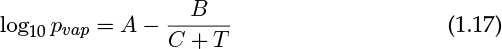
Values of the constants A, B, and C are tabulated in many books (for example, Reid et al., 1987) and websites. The units are often in mm Hg for vapor pressure and temperature (T) is in degrees Celsius rather than in standard S.I. units. Hence caution must be exercised when extracting these values from the literature.
1.4.3 Liquid–Liquid Interface: Partition Constant
A simple partition constant (denoted as mA for species A) is often used to describe the interfacial equilibrium between two liquids:
yA,i = mAxA,i
where yA,i is the interfacial mole fraction in one of the liquid phases and xA,i is the interfacial mole fraction at the interface of the second liquid. The partition coefficient, in turn, is related to ratio of activity coefficients of A in the two phases:
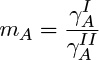
The value of this coefficient is often predicted using thermodynamic models for activity coefficients.
1.4.4 Fluid–Solid Interface: Adsorption Isotherm
Thermodynamic jump at gas–solid or liquid–solid interfaces is defined in a similar manner, using an adsorption equilibrium constant that has a same status as the solubility or partition coefficient. Often a linear relation is used: qA = KACA where qA is the equilibrium concentration of A in the solid phase and CA is its concentration in the gas phase. KA is referred to as the (linear) adsorption equilibrium constant.
1.4.5 Nonlinear Equilibrium Models
A note is in order regarding the linear models described in the previous sections. These models are widely used, even when they do not hold exactly for simplification of the models. However, more complex models are needed to describe equilibrium in non-ideal liquid mixtures—and in systems where there is a strong adsorbed layer due to differences between the interfacial tensions of various species dissolved in the liquids. This layer often has completely different property from the two liquids in contact and is sometimes referred to as a microphase.
On a similar note for fluid–solid systems, linear adsorption equilibria are often used, although these are actually the limiting case of nonlinear relations (the classical Langmuir equation and other isotherms are described in Section 29.3). The linear relation is a good approximation for dilute systems. More generally, the Langmuir isotherm is used to represent equilibrium for gas–solid and liquid–solid systems for concentrated solutions. For gases that undergo a reaction in the liquid, the solubility has to be viewed as the first step for the dissolution equilibrium constant—for example, A(gas) to A(aq) equilibrium. Dissolved gas may further react; hence the quantity of gas absorbed will also depend on the equilibrium constant for these reactions, which are accounted for separately. This value can exceed that calculated using the solubility parameter alone. An example of such system is SO2 in water, where the dissolved SO2 undergoes reaction to form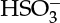 
or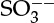 
ions depending on the pH of the solution.