- 1.1 What Is Mass Transfer?
- 1.2 Preliminaries: Continuum and Concentration
- 1.3 Flux Vector
- 1.4 Concentration Jump at Interface
- 1.5 Application Examples
- 1.6 Basic Methodology of Model Development
- 1.7 Conservation Principle
- 1.8 Differential Models
- 1.9 Macroscopic Scale
- 1.10 Mesoscopic or Cross-Section Averaged Models
- 1.11 Compartmental Models
- Summary
- Review Questions
- Problems
This chapter is from the book
This chapter is from the book
This chapter is from the book
1.3 Flux Vector
Mass transfer can be caused by diffusion and bulk motion of the system as a whole. To describe the rate of mass transfer, we need the definition of flux.
1.3.1 Molar and Mass Flux: Definition
Consider a plane of a differential area ΔA with its normal pointing in the x-direction. The quantity (in moles or mass) of a species A crossing this plane per unit area per unit time is defined as the flux component in this direction. This is commonly denoted as NAx with units of moles A per unit area per unit time (see Figure 1.1). The first subscript indicates the species being transported, while the second subscript indicates the orientation of the plane or the surface under consideration. Similar definitions apply for the flux component in the y- and z-directions. Thus NAy represents the moles crossing a plane oriented in the +y direction per unit time per unit area, and NAz is defined in a similar manner. The three components together constitute a vector, with the molar flux vector usually denoted as NA, and the units being mol of A/m2 s.
)
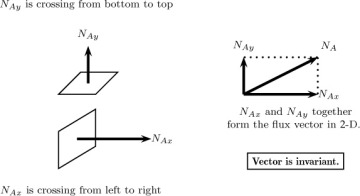
Figure 1.1 Notion of flux vector and representation of its components. The flux vector is uniquely defined as any given point, while the components depend on the constructed coordinate system. Thus, if the coordinates are rotated, the components will be different but the flux vector will be the same.
If we use the mass units, we can define a mass flux vector, which is usually denoted as nA, with the units being kg A/m2 s.
The flux vector is unique at a given point, whereas the components NAx and so forth depend on the orientation of the x-axis and other dimensions. Thus the components can change in magnitude if, for example, the coordinates are rotated. This will not alter the results in any way since the flux vector is frame indifferent. Similarly, the flux components can be defined in cylindrical, spherical, or other body-fitted coordinate systems and used for the specified geometry. The flux results both from diffusion and due to the flow rate across the control surface and hence the flux are referred to as combined flux. For modeling purposes, it is necessary to split this entity into diffusion flux and convection flux. Thus
Combined flux = convection flux + diffusion flux
This partitioning, which is illustrated in Figure 1.2, is not unique. Rather, it will depend on which value is assigned to the convection flux, as will be shown in the next section.
)
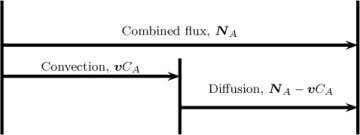
Figure 1.2 Partitioning of the combined flux into diffusion and convection flux. The total flux is fixed from the conditions prevailing at that point. In contrast, the partitioning is not unique and depends on the definition of the mixture velocity, v.
1.3.2 Convection Flux
Convection is transport due to flow, and convection flux can be easily calculated if the velocity of flow is known. Thus, if there is a velocity vx in the x-direction, then a flux of vxCA results from this velocity in the x-direction and is referred to as a convection flux. In general, for the 3-D case the convection flux depends on (a suitably defined) mixture velocity v and is defined as
Convection flux vector = vCA
Note that the mixture velocity in a multicomponent system is not uniquely defined, unlike in a single-component system. This topic is discussed further in Chapter 5. The point to note here is that the convection flux depends on which definition of the mixture velocity is used. The diffusion flux is correspondingly adjusted since the total flux at any point is fixed.
1.3.3 Diffusion Flux
Diffusion is a tendency for a system to approach equilibrium conditions. This can be considered as a result of molecular-level motion when looked from a continuum point of view. Diffusion is therefore also referred to as molecular transport. It must be modeled based on empirical observation, with the resulting model being called a constitutive model. This result is system specific, as there is no universal law to describe the process of diffusive mass transfer. However, it is common to model diffusion by Fick’s law, which states that the (molar diffusive) flux of A is proportional to the concentration gradient of A, dCA/dx:
Here JAx is the diffusion flux of A in the x-direction. Note that the law implies that the diffusion occurs in the direction of negative concentration gradient— that is, from a region of higher concentration to a region of lower concentration. This is similar to heat flowing from a hot body to a cold body. The constant of proportionality DA is called the diffusion coefficient of A. It has the units of m2/s.
More generally speaking, the gradients in the chemical potential can be viewed as causing mass transfer, such that use of these concepts leads to more complex expressions for the diffusive flux. These complexities are addressed in Chapter 7. One consequence of such models is that DA may not have a constant value over the entire concentration range, but rather may be a function of concentration, especially for a non-ideal liquid mixture. Another consequence is that in some cases, the diffusion can occur counter to the direction of negative concentration gradient. These complex effects and models of them will be deferred to Chapter 7.
Note: A more precise definition of diffusion flux is provided in Chapter 5 and requires a more precise definition of the velocity of a multicomponent mixture. The point to note at this stage is that in a multicomponent system, the mixture velocity is not uniquely defined, unlike in a single-component system. The diffusion flux is defined correspondingly, with the mixture velocity as the frame of reference. Also, Fick’s law (shown by Equation 1.12) applies to a system in which the total concentration C remains constant at various points in the system. A more general representation and the topic of diffusion in systems with total constant density are deferred to Chapter 5. Nevertheless, for many applications the simple Fick’s model for diffusion shown here is widely used.
Generalization of Fick’s law to the 3-D case is accomplished by using the notion of the gradient of a scalar:
where ∇CA is the concentration gradient vector.
Typical Values of Diffusivity
The range of values of the diffusion coefficient depends on the phase in which transport is taking place. The range of values are shown in Table 1.1.
Table 1.1 Order of Magnitude Values of the Diffusion Coefficient
System |
DA Values in m2/s |
Gas in gas |
10–5 to 10–4 |
Gas in porous solid |
10–6 to 10–5 |
Gas in narrow pores |
10–8 to 10–6 |
Liquid in liquid |
10–10 to 10–9 |
Liquid in porous solid |
10–11 to 10–10 |
Solid in solid |
10–12 to 10–17 |
Note that the convection flux is proportional to the concentration, while the diffusion flux is proportional to the concentration gradient.
Although convection and diffusion are the two fundamental modes of mass transport, additional phenomena such as turbulent diffusion and dispersion are also used. These are not independent mechanisms, but rather reflect the combined effects of diffusion and convection. A brief description is provided here, but detailed discussion of these topics is deferred to later chapters (4 and 12).
Turbulent Diffusion
Convective transport is due to fluid motion. Fluid flow can be either laminar, turbulent, or transitional, depending on the flow rate, viscosity, and other parameters. For steady-state laminar flow, the velocity is time independent and the convection flux based on the time-independent velocity applies. However, in turbulent flow, random fluctuating components of velocity are superimposed on the main flow. The convective mass transport due to the fluctuating part of velocity, when averaged over time, is usually modeled as an additional mode of transport, referred to as eddy diffusion or turbulent diffusion. Thus the turbulent diffusion is a consequence of the concept of time averaging widely used in study of turbulent transport and is not an independent mass transport mechanism.
Diffusion can be viewed as manifestation of random molecular motion, while turbulent diffusion can be viewed as the result of random bulk motion of the eddies. Diffusion brings in species from a region of higher concentration to a region of lower concentration. Similarly, turbulent eddies bring in species from a region of higher concentration to a region of lower concentration and the process can be modeled by an equation similar to Fick’s law:
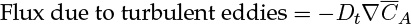
where Dt is the turbulent diffusivity, also known as eddy diffusivity. Turbulent diffusivity is a flow-dependent property rather than a molecular property. The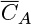 
is a time-averaged value of the fluctuating concentration, which is a characteristic of turbulent transport. Models to calculate Dt are provided in Chapter 12. (This quantity is commonly defined as the time average of the product of velocity fluctuation and the concentration fluctuation.)
Dispersion
Consider the flow of a fluid in a pipe. There is a velocity profile across the tube radius. The velocity at the wall is zero, while that at the center is at its maximum. The contribution of the convection resulting from this velocity profile and the associated diffusion, when averaged across the pipe cross-section, can be modeled as another mode of mass transfer, referred to as dispersion. Thus the dispersion is a consequence of the concept of cross-sectional averaging, which is widely used in mesoscopic model analysis (described in more detail in Chapters 4 and 14) of mass transport, rather than an independent mass transport mechanism.