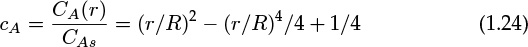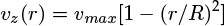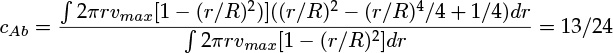- 1.1 What Is Mass Transfer?
- 1.2 Preliminaries: Continuum and Concentration
- 1.3 Flux Vector
- 1.4 Concentration Jump at Interface
- 1.5 Application Examples
- 1.6 Basic Methodology of Model Development
- 1.7 Conservation Principle
- 1.8 Differential Models
- 1.9 Macroscopic Scale
- 1.10 Mesoscopic or Cross-Section Averaged Models
- 1.11 Compartmental Models
- Summary
- Review Questions
- Problems
This chapter is from the book
This chapter is from the book
This chapter is from the book
1.10 Mesoscopic or Cross-Section Averaged Models
Mesoscopic models are useful when there is a principal direction over which the flow takes place, as in pipe flow, for instance. Control volume is taken as differential in this direction but assumed to span the entire cross-section in the cross-flow directions (Figure 1.12). The rationale for this assumption is as follows: The concentration variation in the flow direction is more significant, meaning it changes significantly from inlet to outlet, rather than in the radial direction. Changes in the radial direction at any fixed axial position may not be very large. Hence the mesoscopic control volume shown in Figure 1.12 is adequate in lieu of a complete differential model. The key point to note is that the information on the radial variation of concentration and its effect of the various terms in the conservation model is lost with this kind of model. Hence an appropriate closure model is needed the supplement the information lost due to area or radial averaging. More details on this approach are provided in Chapter 4. Here, we provide some simple examples of closure models used for this level of modeling.
)
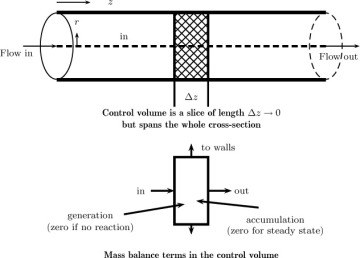
Figure 1.12 Illustration of the mesoscopic control volume for analysis of mass transfer processes in pipe flow. All of the terms in the mass balance are integrals of (unresolved) pointwise values. Hence model or closure for these terms is needed.
1.10.1 Solid Dissolution from a Wall
Consider the mesocopic model applied to a simple system of solid dissolution from a wall in a tube shown in Figure 1.12. Here we have a pipe coated with a dissolving or subliming solute material; a fluid is flowing in the pipe. The concentration of the solute is to be calculated as a function of the length. Two specific examples are a naphthalene-coated pipe with air flow; a pipe coated with benzoic acid (which is a solid at room temperature) with water flow. We assume steady state so that the accumulation is zero.
The conservation law (in – out = 0) is now represented as
in from flow at z + in by transported from the walls –out from flow at z + Δz = 0
To calculate the in and out terms due to flow, we must recognize that the velocity can vary across the cross-section. Concentration also varies along the pipe, with the maximum concentration found at the dissolving pipe wall. The flow can be laminar or turbulent. Laminar flow of a Newtonian fluid has a parabolic profile, whereas the profile is very steep in turbulent flow as shown in Figure 1.13. The velocity for the turbulent flow is the time-averaged value, a concept that is discussed more fully in Chapter 12.
)
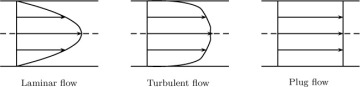
Figure 1.13 Schematic of axial velocity profiles for laminar, turbulent, and plug flow in a pipe as a function of radial position.
A cross-sectionally averaged velocity is an useful quantity and is defined as
which is the integral average of the local velocity. The volumetric flow rate is then equal to 〈v〉 A; v is the axial velocity.
The plug flow shown in the Figure 1.13 is an idealization that is often used to simplify the models. Here the velocity is assumed to be the same at each local radial position. Consequently, the cross-sectional average velocity is also equal to the local velocity.
The in and out terms are the integral average of the axial flux values. The flux component in the axial direction is primarily due to convection and is locally equal to vCA. For a small differential area, ΔA, the moles of A crossing is therefore equal to vCA ΔA. Hence the moles crossing over the entire tube area is the integral of the product of local velocity and the local concentration:
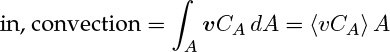
where the notation 〈...〉 is used as shorthand to indicate the averaged value of any quantity within the brackets. Thus we define
We need 〈vCA〉 to evaluate the in and out terms, which cannot be calculated because local concentration values are not available at the meso-level. Hence we define and use an average concentration. This average concentration is called the cup mixing average concentration, of the flow weighted average. It is denoted as CAb and defined as follows:
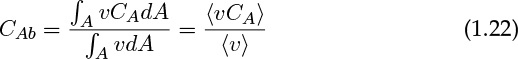
Hence
The in and out terms are then represented simply as A 〈v〉 CAb. Thus the cup mixing concentration is used as the representative concentration variable in the context of our mesoscopic model. The local concentration has no relevance because the local information is not available. Note: In the context of the meso-level model, the notation CA is used in many books as a simpler notation; by implication, this is the cup mixed average value and should be interpreted accordingly. The results in such models are the variation of the cup mixing concentration with the axial distance.
Example 1.2 shows a calculation of the cup mixing concentration to clarify the definition. Here we assume that the radial variation is known from other methods, such as from a differential model or by experimental measurements.
Example 1.2 Cup Mixing Concentration
A pipe wall is coated with a solute that dissolves into the flowing liquid. The radial variation of the concentration of the dissolved solute in the liquid at a particular axial position was found to be
where CA is the local concentration at radial position r, CAs is the saturation solubility of the solid, and R is the pipe radius. The term cA is the scaled or dimensionless concentration.
Find the center concentration, the concentration near the pipe wall, and the cup mixing concentration. Flow is laminar and the liquid is Newtonian.
Solution
The (dimensionless) center concentration is 1/4 by substitution of r = 0.
The concentration near the wall is equal to 1 by substitution of r = R. Liquid near the wall is saturated, so the dimensionless concentration is one as expected.
The cup mixing is done by using Equation 1.22. The weighting factor of 2πrvz Δr is used in the integral because ΔA = 2πr Δr for a differential annular cross-section. Here vz is the local axial velocity—that is, the velocity at location r. For laminar flow of a Newtonian fluid, this is a parabolic function of r. From fluid dynamics, the following relation is obtained:
Using this information in Equation 1.22, the scaled cup mixing concentration is the ratio of the following integrals:
Having defined the in and out terms using the cup mixing concentration, we need an expression for the transport rate to the walls so as to close the model. This is done by defining and using a mass transfer coefficient. It is common practice to use the cup mixing concentration as the representative concentration away from the solid; the driving force for mass transfer is then defined using (CAb – CAw) as the driving force. Hence the mass transfer rate is defined as
NAw = km(CAb – CAw)
The mass transfer coefficients are available for a large number of flows (such as pipe flows) and, in turn, this approach to modeling is widely used in practice. The mesoscopic formulation can be cast into mathematical framework to account for variation of the concentration (cup mixing) as a function of axial position. Further details and the mathematical details follow in Chapter 4. At this stage, however, you should be able to appreciate the essential concepts that go into the construction of mesoscopic models.
1.10.2 Tubular Flow Reactor
Another common application of the meso-modeling concept is the tubular flow reactor. This is a pipe or channel in which a homogeneous chemical reaction is taking place. We will show that not only the cup mixing concentration is needed, but also another average, the cross-sectional average.
Let us start with the conservation principle in words:
in – out + generation = 0
The generation is the average of the local rate:
generation = (A Δx) 〈RA〉
where
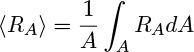
For a first-order reaction, for example, RA = –k1CA, where CA is the local concentration. Hence
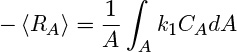
To incorporate this into the conservation law, it is customary to define and use the the cross-sectional average concentration:
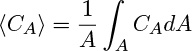
Hence the generation term (first order) to be used in the reactor model is –(AΔx)k1 〈CA〉.
In and out terms are A 〈v〉 CAb as for the solid dissolution. Thus the conservation law in mathematical terms is
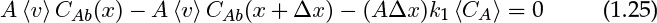
In the limit Δx → 0, this produces the following differential equation:
We find that both the cup mixing and the cross-sectional average appear in the reactor model. Some closure relationship is needed, however, and the commonly used closure models are the plug flow model and the axial dispersion model.
Plug Flow Model
The plug flow model is an idealized reactor model in which the velocity is assumed to be constant, as shown in the Figure 1.13. The cup mixing and the cross-sectional averages are the same since the velocity profile is uniform and, therefore, CAb = 〈CA〉. Only the cross-sectional concentration is needed; that is, no additional closure is needed. Equation 1.26 reduces to
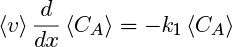
Axial Dispersion Model
The actual reactor may not be a plug flow model, in which case the deviation from plug flow can be modeled by including an additional correction term. The resulting model is known as the axial dispersion model. The representation for the in or out term is
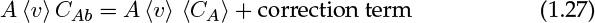
The first term on the right side is the mole flow crossing a cross-section if the plug flow prevails. The second term is a correction term. This system is modeled as though some diffusion type of mechanism is superimposed on the plug flow value. Hence
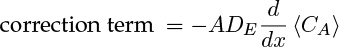
where DE is called the axial dispersion coefficient. This is only a model, and not a fundamental principle, but nevertheless it provides an important crutch to proceed further in modeling these systems. The axial dispersion coefficient is a commonly used parameter when modeling both reactors and separation processes. Details of the origin of this term and the calculation and application of this concept are discussed in Section 14.2. For now, recognize that the dispersion model closure is
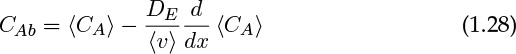
The key points to appreciate from this section are the various definitions and closures that are needed in the context of meso-scale models.
Now we discuss models at an even higher level of simplicity—namely, the compartmental models.