- Language of Mathematics
- Coordinate Spaces and Moving among Them
- Points, Vectors, and Vector Operations
- Normalization and Unit Vectors
- Pythagorean Theorem
- Sine, Cosine, and Tangent
- Matrices and Matrix Operations
- Transformations: Scale, Translation, Rotation, Projection
- Summary
Transformations: Scale, Translation, Rotation, Projection
Now that you have a basic feel for how matrix operations work, it’s time to explain how you use them in the context of graphics programming. One large part of graphics programming—and one of the reasons it’s so fascinating and powerful—is its ability to implement change. You can change the size, location, spin, and so on, of objects in a scene. This is how you get interactive computer graphics and not just a pretty picture to put on your wall. All of these operations are known as transformations, and all of them can be expressed as matrices.
Scale Matrix
Now that you have a grasp on how to set up your matrices, let’s move on to actually changing some of the values and see a change to your matrix. The first matrix we talk about is the scale matrix. The scale matrix isn’t much different from the identity matrix.
The scale matrix has all the same zeros as the identity matrix, but it doesn’t necessarily keep using the ones across the diagonal. You are trying to decide how to scale your coordinate, and you don’t want the default scale value to be 1. Here is the scale matrix:
[ Sx 0 0 0 0 Sy 0 0 0 0 Sz 0 0 0 0 1 ]
For Sx, Sy, and Sz, you determine how much you want to scale that coordinate by and you enter that value into the matrix. Nothing else changes or is affected. This is the easiest matrix to deal with besides the identity matrix because, in a sense, the identity matrix can be a scale matrix. It just has a scale of 1.
Translation Matrix
The next matrix we talk about is the translation matrix. The translation matrix tweaks the identity matrix somewhat. We already established that the identity matrix returns the same coordinate that you started with. The translation matrix goes a little further and applies a translation value to the coordinate.
The translation matrix looks the same as the identity matrix, but the last column is a little different. The last column applies an amount of change for the x, y, and z coordinates:
[ 1 0 0 Tx 0 1 0 Ty 0 0 1 Tz 0 0 0 1 ]
Let’s look back at our (3, 4, 0) coordinate. This coordinate would be written out as:
[ 3 4 0 1 ]
Let’s say you want to adjust the x value by 3. You don’t want anything else in the coordinate to change; you just want the x value to increase by 3. The translation matrix would look like this:
[ 1 0 0 3 0 1 0 0 0 0 1 0 0 0 0 1 ]
The bottom three rows of the matrix are the same as the identity matrix, so don’t worry about them for now. Just look at how this translation affects the first coordinate:
(3 * 1) + (4 * 0) + (0 * 0) + (1 * 3) = 6
What happens if you try to apply a translation to a vector? Nothing. Vectors don’t represent a specific point in space and consequently cannot be affected. Let’s make our test coordinate a vector:
[ 3 4 0 0 ]
Now let’s apply a crazy translation to it:
[ 1 0 0 42 0 1 0 108 0 0 1 23 0 0 0 1 ] C1 = (3 * 1) + (4 * 0) + (0 * 0) + (42 * 0) = 3 C2 = (3 * 0) + (4 * 1) + (0 * 0) + (108 * 0) = 4 C3 = (3 * 0) + (4 * 0) + (0 * 0) + (23 * 0) = 0 C4 = (3 * 0) + (4 * 0) + (0 * 0) + (0 * 0) = 0
Because that last value in the vector is 0, it doesn’t matter how radically you try to translate a vector—it’s not going to change. This is all well and good, but why would we want to do it? What does understanding the translation matrix allow us to do?
Rotation Matrix
Movement is an important part of interactive 3D graphics. Sometimes, movement is unfettered, like a ball, and moves in all directions, but there are many subsets of movement that revolve around rotation. If you are animating a door swinging open, there is a limited range of motion available for that action as the door rotates around the edge where the hinges are. This movement can be calculated in a matrix operation.
If you read the section “Sine, Cosine, and Tangent,” you learned that you use sine and cosine to determine angles of a triangle. If you think of the initial position of the vector as one side of a triangle and the desired final position as another, you can take advantage of the triangle operations to figure out how to describe the rotation of the vector in your matrix.
An example of a rotation matrix would look something like this:
[ 1 0 0 0 0 cosθ -sinθ 0 0 sinθ cosθ 0 0 0 0 1 ]
This matrix describes an angle of rotation around the x-axis. Because the x-axis is acting as the hinge on the door, it does not change. You choose the angle you want to rotate the vector by, and the new y and z coordinates are calculated by applying the sine or cosine of the angle of rotation.
Projection Matrix
The last matrix we discuss is an important one that you need to understand, and that is the projection matrix. In graphics programming, there are two spaces that you use: camera space and world space. World space encompasses every object in a scene. Camera space determines how many of these objects are within the field of view. It’s possible and common for there to be areas of a scene that are not always visible at any given moment. Think about any first-person shooter game. If your character is moving down a hallway, the areas your character passed are no longer in your field of view and should no longer be rendered.
The projection matrix determines the camera space, which is the visible area in a scene, so that the renderer knows to check for objects only in places that will be seen. It also helps determine the clipping area by figuring out if objects are partially off screen and need to be retriangulated. You are making the transition away from thinking about everything in relation to the origin of the model to thinking about the model in relation to the origin of the world space.
Concatenation
So far, we’ve been talking about applying a matrix to a coordinate. But, is it possible to apply one matrix to another matrix? Absolutely. The process of multiplying two matrices together is known as concatenation. Concatenation isn’t limited to just two matrices. In fact, in graphics programming, you will chain many matrix operations, and these can be concatenated into a single matrix.
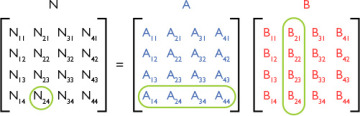
Figure 4.7 How matrix concatenation is calculated
To apply one matrix to another, you take the dot product of the corresponding rows and columns from the two matrices you are multiplying together, as shown in Figure 4.7. For example, if you wanted to find the second value in the fourth row of the new matrix, you would take the dot product of the fourth row of the first matrix and the second column of the second matrix.
If you have more than two matrices, you can still perform this operation. The dot product of the first two matrices creates a temporary matrix that can be applied to the next matrix, and so on. These matrices can then be applied to transform a coordinate. It’s important to note that matrix multiplication usually proceeds from right to left, rather than from left to right, which is what happens when treating vectors as column matrices.