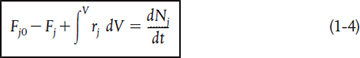- 1.1 The Rate of Reaction, -rA
- 1.2 The General Mole Balance Equation
- 1.3 Batch Reactors (BRs)
- 1.4 Continuous-Flow Reactors
- 1.5 Industrial Reactors
- Summary
- CRE Web Site Materials
- Questions and Problems
This chapter is from the book
This chapter is from the book
This chapter is from the book
1.2 The General Mole Balance Equation
To perform a mole balance on any system, the system boundaries must first be specified. The volume enclosed by these boundaries is referred to as the system volume. We shall perform a mole balance on species j in a system volume, where species j represents the particular chemical species of interest, such as water or NaOH (Figure 1-3).
)
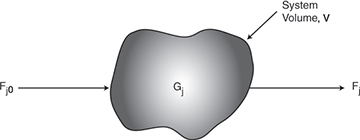
Figure 1-3 Mole balance on species j in a system volume, V.
A mole balance on species j at any instant in time, t, yields the following equation:
)
In this equation, Nj represents the number of moles of species j in the system at time t. If all the system variables (e.g., temperature, catalytic activity, and concentration of the chemical species) are spatially uniform throughout the system volume, the rate of generation of species j, Gj, is just the product of the reaction volume, V, and the rate of formation of species j, rj.
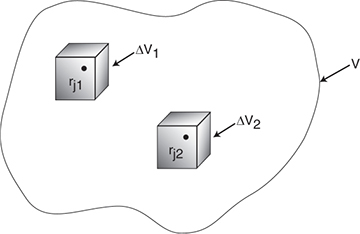
Now suppose that the rate of formation of species j for the reaction varies with position in the system volume. That is, it has a value rj1 at location 1, which is surrounded by a small volume, ΔV1, within which the rate is uniform; similarly, the reaction rate has a value rj2 at location 2 and an associated volume, ΔV2, and so on (Figure 1-4).
)
Figure 1-4 Dividing up the system volume, V.
The rate of generation, ΔGj1, in terms of rj1 and subvolume ΔV1, is
ΔGj1 = rj1 ΔV1
Similar expressions can be written for ΔGj2 and the other system subvolumes, ΔVi. The total rate of generation within the system volume is the sum of all the rates of generation in each of the subvolumes. If the total system volume is divided into M subvolumes, the total rate of generation is
By taking the appropriate limits (i.e., let M → ∞ and ΔV → 0 ) and making use of the definition of an integral, we can rewrite the foregoing equation in the form
From this equation, we see that rj will be an indirect function of position, since the properties of the reacting materials and reaction conditions (e.g., concentration, temperature) can have different values at different locations in the reactor volume.
We now replace Gj in Equation (1-3), i.e.,
by its integral form to yield a form of the general mole balance equation for any chemical species j that is entering, leaving, reacting, and/or accumulating within any system volume V.
)
From this general mole balance equation, we can develop the design equations for the various types of industrial reactors: batch, semibatch, and continuous-flow Upon evaluation of these equations, we can determine the time (batch) or reactor volume (continuous-flow) necessary to convert a specified amount of the reac-tants into products.