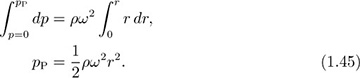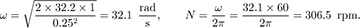- 1.1 Fluid Mechanics in Chemical Engineering
- 1.2 General Concepts of a Fluid
- 1.3 Stresses, Pressure, Velocity, and the Basic Laws
- 1.4 Physical Properties-Density, Viscosity, and Surface Tension
- 1.5 Units and Systems of Units
- 1.6 Hydrostatics
- 1.7 Pressure Change Caused by Rotation
- Problems for Chapter 1
This chapter is from the book
This chapter is from the book
This chapter is from the book
1.7 Pressure Change Caused by Rotation
Finally, consider the shape of the free surface for the situation shown in Fig. 1.20(a), in which a cylindrical container, partly filled with liquid, is rotated with an angular velocity ω—that is, at N = ω/2π revolutions per unit time. The analysis has applications in fuel tanks of spinning rockets, centrifugal filters, and liquid mirrors.
)
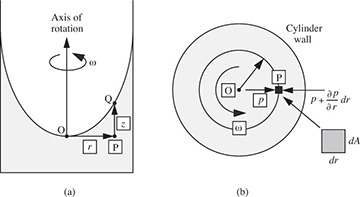
Fig. 1.20 Pressure changes for rotating cylinder: (a) elevation, (b) plan.
Point O denotes the origin, where r = 0 and z = 0. After a sufficiently long time, the rotation of the container will be transmitted by viscous action to the liquid, whose rotation is called a forced vortex. In fact, the liquid spins as if it were a solid body, rotating with a uniform angular velocity ω, so that the velocity in the direction of rotation at a radial location r is given by vθ = rω. It is therefore appropriate to treat the situation similar to the hydrostatic investigations already made.
Suppose that the liquid element P is essentially a rectangular box with cross-sectional area dA and radial extent dr. (In reality, the element has slightly tapering sides, but a more elaborate treatment taking this into account will yield identical results to those derived here.) The pressure on the inner face is p, whereas that on the outer face is p + (∂p/∂r)dr. Also, for uniform rotation in a circular path of radius r, the acceleration toward the center O of the circle is rω2. Newton’s second law of motion is then used for equating the net pressure force toward O to the mass of the element times its acceleration:
)
Note that the use of a partial derivative is essential, since the pressure now varies in both the horizontal (radial) and vertical directions. Simplification yields the variation of pressure in the radial direction:
)
so that pressure increases in the radially outward direction.
Observe that the gauge pressure at all points on the interface is zero; in particular, pO = pQ = 0. Integrating from points O to P (at constant z):
)
However, the pressure at P can also be obtained by considering the usual hydrostatic increase in traversing the path QP:
)
Elimination of the intermediate pressure pP between Eqns. (1.45) and (1.46) relates the elevation of the free surface to the radial location:
)
Thus, the free surface is parabolic in shape; observe also that the density is not a factor, having been canceled from the equations.
There is another type of vortex—the free vortex—that is also important, in cyclone dust collectors and tornadoes, for example, as discussed in Chapters 4 and 7. There, the velocity in the angular direction is given by vθ = c/r, where c is a constant, so that vθ is inversely proportional to the radial position.
Example 1.8—Overflow from a Spinning Container
A cylindrical container of height H and radius a is initially half-filled with a liquid. The cylinder is then spun steadily around its vertical axis Z-Z, as shown in Fig. E1.8. At what value of the angular velocity ω will the liquid just start to spill over the top of the container? If H = 1 ft and a = 0.25 ft, how many rpm (revolutions per minute) would be needed?
)
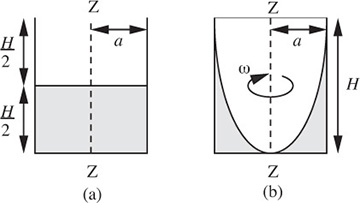
Fig. E1.8 Geometry of a spinning container: (a) at rest, (b) on the point of overflowing.
Solution
From Eqn. (1.47), the shape of the free surface is a parabola. Therefore, the air inside the rotating cylinder forms a paraboloid of revolution, whose volume is known from calculus to be exactly one-half of the volume of the “circumscribing cylinder,” namely, the container.8 Hence, the liquid at the center reaches the bottom of the cylinder just as the liquid at the curved wall reaches the top of the cylinder. In Eqn. (1.47), therefore, set z = H and r = a, giving the required angular velocity:
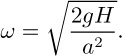
For the stated values:
)