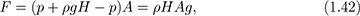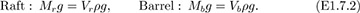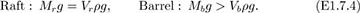- 1.1 Fluid Mechanics in Chemical Engineering
- 1.2 General Concepts of a Fluid
- 1.3 Stresses, Pressure, Velocity, and the Basic Laws
- 1.4 Physical Properties-Density, Viscosity, and Surface Tension
- 1.5 Units and Systems of Units
- 1.6 Hydrostatics
- 1.7 Pressure Change Caused by Rotation
- Problems for Chapter 1
1.6 Hydrostatics
Variation of pressure with elevation. Here, we investigate how the pressure in a stationary fluid varies with elevation z. The result is useful because it can answer questions such as “What is the pressure at the summit of Mt. Annapurna?” or “What forces are exerted on the walls of an oil storage tank?” Consider a hypothetical differential cylindrical element of fluid of cross-sectional area A, height dz, and volume Adz, which is also surrounded by the same fluid, as shown in Fig. 1.13. Its weight, being the downward gravitational force on its mass, is dW = ρA dz g. Two completely equivalent approaches will be presented:
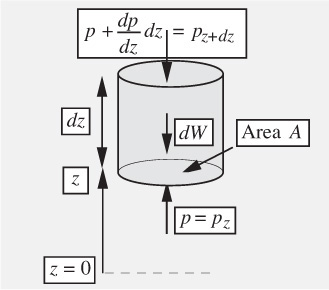
Fig. 1.13 Forces acting on a cylinder of fluid.
Method 1. Let p denote the pressure at the base of the cylinder; since p changes at a rate dp/dz with elevation, the pressure is found either from Taylor’s expansion or the definition of a derivative to be p + (dp/dz)dz at the top of the cylinder.7 (Note that we do not anticipate a reduction of pressure with elevation here; hence, the plus sign is used. If, indeed—as proves to be the case—pressure falls with increasing elevation, then the subsequent development will tell us that dp/dz is negative.) Hence, the fluid exerts an upward force of pA on the base of the cylinder and a downward force of [p + (dp/dz)dz]A on the top of the cylinder.
Next, apply Newton’s second law of motion by equating the net upward force to the mass times the acceleration—which is zero, since the cylinder is stationary:
Cancellation of pA and division by Adz leads to the following differential equation, which governs the rate of change of pressure with elevation:
Method 2. Let pz and pz+dz denote the pressures at the base and top of the cylinder, where the elevations are z and z + dz, respectively. Hence, the fluid exerts an upward force of pzA on the base of the cylinder, and a downward force of pz+dzA on the top of the cylinder. Application of Newton’s second law of motion gives:
Isolation of the two pressure terms on the left-hand side and division by Adz gives:
As dz tends to zero, the left-hand side of Eqn. (1.32) becomes the derivative dp/dz, leading to the same result as previously:
The same conclusion can also be obtained by considering a cylinder of finite height Δz and then letting Δz approach zero.
Note that Eqn. (1.30) predicts a pressure decrease in the vertically upward direction at a rate that is proportional to the local density. Such pressure variations can readily be detected by the ear when traveling quickly in an elevator in a tall building or when taking off in an airplane. The reader must thoroughly understand both the above approaches. For most of this book, we shall use Method 1, because it eliminates the steps of taking the limit of dz → 0 and invoking the definition of the derivative.
Pressure in a liquid with a free surface. In Fig. 1.14, the pressure is ps at the free surface, and we wish to find the pressure p at a depth H below the free surface—of water in a swimming pool, for example.
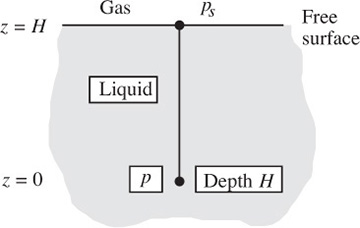
Fig. 1.14 Pressure at a depth H.
Separation of variables in Eqn. (1.30) and integration between the free surface (z = H) and a depth H (z = 0) gives:
Assuming—quite reasonably—that ρ and g are constants in the liquid, these quantities may be taken outside the integral, yielding:
which predicts a linear increase of pressure with distance downward from the free surface. For large depths, such as those encountered by deep-sea divers, very substantial pressures will result.
Example 1.3—Pressure in an Oil Storage Tank
What is the absolute pressure at the bottom of the cylindrical tank of Fig. E1.3, filled to a depth of H with crude oil, with its free surface exposed to the atmosphere? The specific gravity of the crude oil is 0.846. Give the answers for (a) H = 15.0 ft (pressure in lbf/in2) and (b) H = 5.0 m (pressure in Pa and bar). What is the purpose of the surrounding dike?
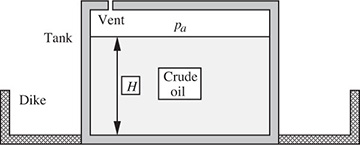
Fig. E1.3 Crude oil storage tank.
Solution
(a) The pressure is that of the atmosphere, pa, plus the increase due to a column of depth H = 15.0 ft. Thus, setting ps = pa, Eqn. (1.34) gives:
The reader should check the units, noting that the 32.2 in the numerator is g [=] ft/s2 and that the 32.2 in the denominator is gc [=] lbm ft/lbf s2.
(b) For SI units, no conversion factors are needed. Noting that the density of water is 1,000 kg/m3 and that pa ≐ 1.01 × 105 Pa absolute:
p = 1.01 × 105 + 0.846 × 1,000 × 9.81 × 5.0 = 1.42 × 105 Pa = 1.42 bar.
In the event of a tank rupture, the dike contains the leaking oil and facilitates prevention of spreading fire and contamination of the environment.
Epilogue
When he arrived at work in an oil refinery one morning, the author saw first-hand the consequences of an inadequately vented oil-storage tank. Rain during the night had caused partial condensation of vapor inside the tank, whose pressure had become sufficiently lowered so that the external atmospheric pressure had crumpled the steel tank just as if it were a flimsy tin can. The refinery manager was not pleased.
Example 1.4—Multiple Fluid Hydrostatics
The U-tube shown in Fig. E1.4 contains oil and water columns, between which there is a long trapped air bubble. For the indicated heights of the columns, find the specific gravity of the oil.
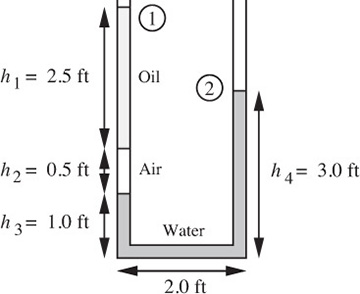
Fig. E1.4 Oil/air/water system.
Solution
The pressure p2 at point 2 may be deduced by starting with the pressure p1 at point 1 and adding or subtracting, as appropriate, the hydrostatic pressure changes due to the various columns of fluid. Note that the width of the U-tube (2.0 ft) is irrelevant, since there is no change in pressure in the horizontal leg. We obtain:
in which ρo, ρa, and ρw denote the densities of oil, air, and water, respectively. Since the density of the air is very small compared to that of oil or water, the term containing ρa can be neglected. Also, p1 = p2, because both are equal to atmospheric pressure. Equation (E1.4.1) can then be solved for the specific gravity so of the oil:
Pressure variations in a gas. For a gas, the density is no longer constant but is a function of pressure (and of temperature—although temperature variations are usually less significant than those of pressure), and there are two approaches:
For small changes in elevation, the assumption of constant density can still be made, and equations similar to Eqn. (1.34) are still approximately valid.
For moderate or large changes in elevation, the density in Eqn. (1.30) is given by Eqn. (1.7) or (1.8), ρ = Mwp/RT or ρ = Mwp/ZRT, depending on whether the gas is ideal or nonideal. It is understood that absolute pressure and temperature must always be used whenever the gas law is involved. A separation of variables can still be made, followed by integration, but the result will now be more complicated because the term dp/p occurs, leading—at the simplest (for an isothermal situation)—to a decreasing exponential variation of pressure with elevation.
Example 1.5—Pressure Variations in a Gas
For a gas of molecular weight Mw (such as the earth’s atmosphere), investigate how the pressure p varies with elevation z if p = p0 at z = 0. Assume that the temperature T is constant. What approximation may be made for small elevation increases? Explain how you would proceed for the nonisothermal case, in which T = T(z) is a known function of elevation.
Solution
Assuming ideal gas behavior, Eqns. (1.30) and (1.7) give:
Separation of variables and integration between appropriate limits yields:
since Mwg/RT is constant. Hence, there is an exponential decrease of pressure with elevation, as shown in Fig. E1.5:
Since a Taylor’s expansion gives e−x = 1 – x + x2/2 – ..., the pressure is approximated by:
For small values of Mwgz/RT, the last term is an insignificant second-order effect (compressibility effects are unimportant), and we obtain:
in which ρ0 is the density at elevation z = 0; this approximation—essentially one of constant density—is shown as the dashed line in Fig. E1.5 and is clearly applicable only for a small change of elevation. Problem 1.19 investigates the upper limit on z for which this linear approximation is realistic. If there are significant elevation changes—as in Problems 1.16 and 1.30—the approximation of Eqn. (E1.5.5) cannot be used with any accuracy. Observe with caution that the Taylor’s expansion is only a vehicle for demonstrating what happens for small values of Mwgz/RT. Actual calculations for larger values of Mwgz/RT should be made using Eqn. (E1.5.3), not Eqn. (E1.5.4).
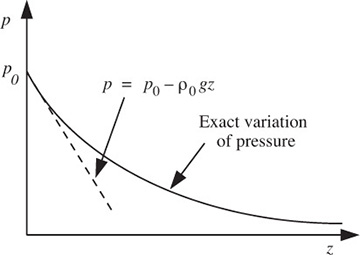
Fig. E1.5 Variation of gas pressure with elevation.
For the case in which the temperature is not constant, but is a known function T(z) of elevation (as might be deduced from observations made by a meteorological balloon), it must be included inside the integral:
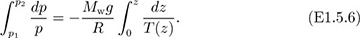
Since T(z) is unlikely to be a simple function of z, a numerical method—such as Simpson’s rule in Appendix A—will probably have to be used to approximate the second integral of Eqn. (E1.5.6).
Total force on a dam or lock gate. Fig. 1.15 shows the side and end elevations of a dam or lock gate of depth D and width W. An expression is needed for the total horizontal force F exerted by the liquid on the dam, so that the latter can be made of appropriate strength. Similar results would apply for liquids in storage tanks. Gauge pressures are used for simplicity, with p = 0 at the free surface and in the air outside the dam. Absolute pressures could also be employed, but would merely add a constant atmospheric pressure everywhere, and would eventually be canceled out. If the coordinate z is measured from the bottom of the liquid upward, the corresponding depth of a point below the free surface is D – z. Hence, from Eqn. (1.34), the differential horizontal force dF on an infinitesimally small rectangular strip of area dA = W dz is:
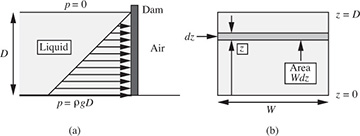
Fig. 1.15 Horizontal thrust on a dam: (a) side elevation, (b) end elevation.
Integration from the bottom (z = 0) to the top (z = D) of the dam gives the total horizontal force:
Horizontal pressure force on an arbitrary plane vertical surface. The preceding analysis was for a regular shape. A more general case is illustrated in Fig. 1.16, which shows a plane vertical surface of arbitrary shape. Note that it is now slightly easier to work in terms of a downward coordinate h.
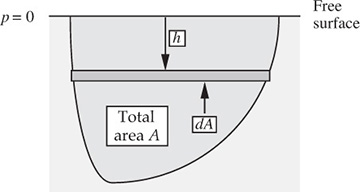
Fig. 1.16 Side view of a pool of liquid with a submerged vertical surface.
Again taking gauge pressures for simplicity (the gas law is not involved), with p = 0 at the free surface, the total horizontal force is:
But the depth hc of the centroid of the surface is defined as:
Thus, from Eqns. (1.37) and (1.38), the total force is:
in which pc is the pressure at the centroid.
The advantage of this approach is that the location of the centroid is already known for several geometries. For example, for a rectangle of depth D and width W:
in agreement with the earlier result of Eqn. (1.36). Similarly, for a vertical circle that is just submerged, the depth of the centroid equals its radius. And, for a vertical triangle with one edge coincident with the surface of the liquid, the depth of the centroid equals one-third of its altitude.
Horizontal pressure force on a curved surface. Fig. 1.17(a) shows the cross section of a submerged surface that is no longer plane. However, the shape is uniform normal to the plane of the diagram.
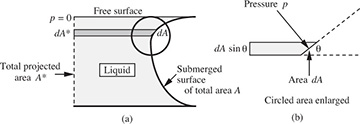
Fig. 1.17 Thrust on surface of uniform cross-sectional shape.
In general, as shown in Fig. 1.17(b), the local pressure force p dA on an element of surface area dA does not act horizontally; therefore, its horizontal component must be obtained by projection through an angle of (π/2 – θ), by multiplying by cos(π/2 – θ) = sin θ. The total horizontal force F is then:
in which dA* = dA sin θ is an element of the projection of A onto the hypothetical vertical plane A*. The integral of Eqn. (1.41) can be obtained readily, as illustrated in the following example.
Example 1.6—Hydrostatic Force on a Curved Surface
A submarine, whose hull has a circular cross section of diameter D, is just submerged in water of density ρ, as shown in Fig. E1.6. Derive an equation that gives the total horizontal force Fx on the left half of the hull, for a distance W normal to the plane of the diagram. If D = 8 m, the circular cross section continues essentially for the total length W = 50 m of the submarine, and the density of sea water is ρ = 1,026 kg/m3, determine the total horizontal force on the left-hand half of the hull.
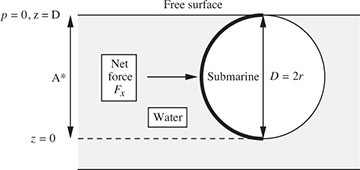
Fig. E1.6 Submarine just submerged in seawater.
Solution
The force is obtained by evaluating the integral of Eqn. (1.41), which is identical to that for the rectangle in Fig. 1.15:
Insertion of the numerical values gives:
Thus, the total force is considerable—about 3.62 × 106 lbf.

Buoyancy forces. If an object is submerged in a fluid, it will experience a net upward or buoyant force exerted by the fluid. To find this force, first examine the buoyant force on a submerged circular cylinder of height H and cross-sectional area A, shown in Fig. 1.18.
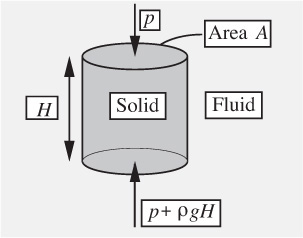
Fig. 1.18 Pressure forces on a submerged cylinder.
The forces on the curved vertical surface act horizontally and may therefore be ignored. Hence, the net upward force due to the difference between the opposing pressures on the bottom and top faces is:
which is exactly the weight of the displaced liquid, thus verifying Archimedes’ law, (the buoyant force equals the weight of the fluid displaced) for the cylinder. The same result would clearly be obtained for a cylinder of any uniform cross section.
Fig. 1.19 shows a more general situation, with a body of arbitrary shape. However, Archimedes’ law still holds since the body can be decomposed into an infinitely large number of vertical rectangular parallelepipeds or “boxes” of infinitesimally small cross-sectional area dA. The effect for one box is then summed or “integrated” over all the boxes and again gives the net upward buoyant force as the weight of the liquid displaced.
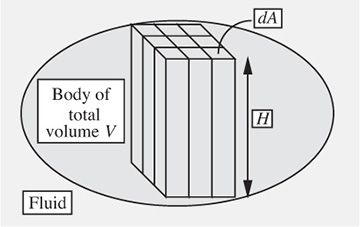
Fig. 1.19 Buoyancy force for an arbitrary shape.
Example 1.7—Application of Archimedes’ Law
Consider the situation in Fig. E1.7(a), in which a barrel rests on a raft that floats in a swimming pool. The barrel is then pushed off the raft and may either float or sink, depending on its contents and hence its mass. The cross-hatching shows the volumes of water that are displaced. For each of the cases shown in Fig. E1.7 (b) and (c), determine whether the water level in the pool will rise, fall, or remain constant, relative to the initial level in (a).
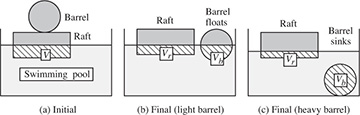
Fig. E1.7 Raft and barrel in swimming pool: (a) initial positions, (b) light barrel rolls off and floats, (c) heavy barrel rolls off and sinks. The cross-hatching shows volumes below the surface of the water.
Solution
Initial state. Let the masses of the raft and barrel be Mr and Mb, respectively. If the volume of displaced water is initially V in (a), Archimedes’ law requires that the total weight of the raft and barrel equals the weight of the displaced water, whose density is ρ:
Barrel floats. If the barrel floats, as in (b), with submerged volumes of Vr and Vb for the raft and barrel, respectively, Archimedes’ law may be applied to the raft and barrel separately:
Addition of the two equations (E1.7.2) and comparison with Eqn. (E1.7.1) shows that:
Therefore, since the volume of the water is constant, and the total displaced volume does not change, the level of the surface also remains unchanged.
Barrel sinks. Archimedes’ law may still be applied to the raft, but the weight of the water displaced by the barrel no longer suffices to support the weight of the barrel, so that:
Addition of the two relations in (E1.7.4) and comparison with Eqn. (E1.7.1) shows that:
Therefore, since the volume of the water in the pool is constant, and the total displaced volume is reduced, the level of the surface falls. This result is perhaps contrary to intuition: since the whole volume of the barrel is submerged in (c), it might be thought that the water level will rise above that in (b). However, because the barrel must be heavy in order to sink, the load on the raft and hence Vr are substantially reduced, so that the total displaced volume is also reduced.
This problem illustrates the need for a complete analysis rather than jumping to a possibly erroneous conclusion.

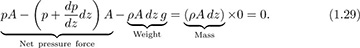

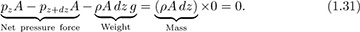






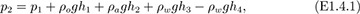
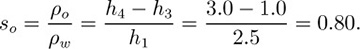

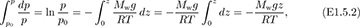

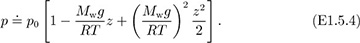
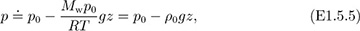
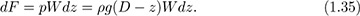
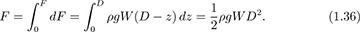
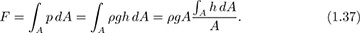


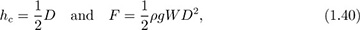
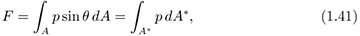
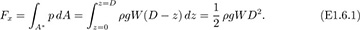
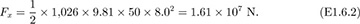
 , “I have found it, I have found it.” To dramatize the effect of a lever, he said, “Give me a place to stand, and I will move the earth.” He considered his most important intellectual contribution to be the determination of the ratio of the volume of a sphere to the volume of the cylinder that circumscribes it. [Now that calculus has been invented, the reader might like to derive this ratio!] Sadly, Archimedes was killed during the capture of Syracuse by the Romans.
, “I have found it, I have found it.” To dramatize the effect of a lever, he said, “Give me a place to stand, and I will move the earth.” He considered his most important intellectual contribution to be the determination of the ratio of the volume of a sphere to the volume of the cylinder that circumscribes it. [Now that calculus has been invented, the reader might like to derive this ratio!] Sadly, Archimedes was killed during the capture of Syracuse by the Romans.