This chapter is from the book
This chapter is from the book
This chapter is from the book
Problems
3.1. Consider the following reaction sequence:
Develop a suitable rate expression for production formation [v = k5 (ES)2] by using (a) the equilibrium approach, and (b) the quasi-steady-state approach.
3.2. Consider the reversible product-formation reaction in an enzyme–catalyzed bioreaction:
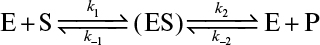
Develop a rate expression for product-formation using the quasi-steady-state approximation and show that
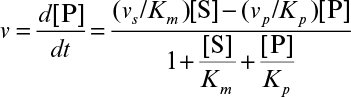
where
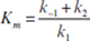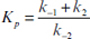and 
and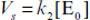 
, 
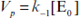.3.3. The enzyme fumarase has the following kinetic constants:
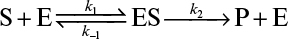
where k1 = 109 M −1 s−1
k−1 = 4.4 × 104 s−1
k2 = 103 s−1
What is the value of the Michaelis constant for this enzyme?
At an enzyme concentration of 10–6 M, what will be the initial rate of product formation at a substrate concentration of 10–3 M?
[Courtesy of D. J. Kirwan from “Collected Coursework Problems in Biochemical Engineering” compiled by H. W. Blanch for 1977 American Society for Engineering Education Summer School.]
3.4. Data on enzymatic degradation of dichlorophenol at different concentrations are given in the following table:
So (mg/l)
30
60
90
120
150
200
250
300
Rate (mg P/l-h)
2.1
3.8
5.7
7.4
8.5
7.1
4.5
2.5
Assuming the substrate-inhibited kinetics is given by the following equation, determine the constants Vm, Km, and KSI:
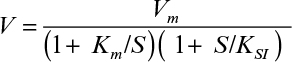
3.5. Biological oxidation of phenylacetic acid is inhibited by propionic acid present in wastewater. The following data were obtained for enzymatic oxidation of phenylacetic acid at different concentrations of propionic acid:
S (mM)
0.25
0.40
0.50
0.60
0.75
1.00
V (mM/l-h), I = 0
1.0
1.7
1.9
2.1
2.4
2.5
V (mM/l-h), I = 1 mM
0.65
1.1
1.3
1.4
1.8
2.2
V (mM/l-h), I = 2 mM
0.55
0.9
1.0
1.3
1.4
1.8
What kind of inhibition is this?
Determine Vm, Km, and KI.
3.6. Hydrogenase enzyme responsible for hydrogen gas synthesis in photoheterotrophic bacteria is activated by the addition of sodium molybdate into the medium. Hydrogen formation rate varies with the Mo concentration as follows:
Rate (mlH2/h)
0.1
0.2
0.3
0.5
0.7
0.9
1.2
Mo (μg/l)
0
10
30
50
80
100
125
Assuming that the activator only affects the maximum reaction rate (Vm), determine the activation constant (KA).
What would be the reaction rate at Mo = 60 μg/l?
3.7. Enzymes are immobilized on flat surfaces of plates in the form of monolayer (or very thin film) and placed in an agitated reactor for enzymatic reaction. The reactor is operated continuously. The bulk substrate concentration is S0 = 200 mg/l at steady state. When the reactor was operated at different agitation speeds, the following data were obtained:
RPM
25
50
100
200
300
400
KL (m/h)
0.18
0.24
0.33
0.42
0.88
2.25
V (mgS/l-h)
30
36
40
41.5
44
45
Determine surface concentration of the substrate for each RPM.
Determine kinetic constants of Vm and Km for the enzymatic reaction.
3.8. The hydration of is catalyzed by carbonic anhydrase as follows:
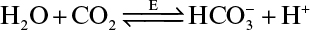
The following data were obtained for the forward and reverse reaction rates at pH 7.1 and an enzyme concentration of 2.8 × 10–9 M:
Hydration
Dehydration
1/v, M −1 (s × 10−3)
[CO2] (M × 10−3)
1/v, M −1 (s × 10−3)
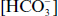(M ×103)36
1.25
95
2
20
2.5
45
5
12
5
29
10
6
20
25
15
v is the initial reaction rate at the given substrate concentration. Calculate the forward and reverse catalytic and Michaelis constants.
(Courtesy of D. J. Kirwan from “Collected Coursework Problems in Biochemical Engineering” compiled by H. W. Blanch for 1977 American Society for Engineering Education Summer School. © American Society for Engineering Education.)
3.9. An inhibitor (I) is added to the enzymatic reaction at a level of 1.0 g/l. The following data were obtained for Km = 9.2 g S/l:
v
S
0.909
20
0.658
10
0.493
6.67
0.40
5
0.333
4
0.289
3.33
0.227
2.5
Is the inhibitor competitive or noncompetitive?
Find KI.
3.10. During a test of kinetics of an enzyme–catalyzed reaction, the following data were recorded:
E0 (g/l)
T (°C)
I (mmol/ml)
S (mmol/ml)
V (mmol/ml-min)
1.6
30
0
0.1
2.63
1.6
30
0
0.033
1.92
1.6
30
0
0.02
1.47
1.6
30
0
0.01
0.96
1.6
30
0
0.005
0.56
1.6
49.6
0
0.1
5.13
1.6
49.6
0
0.033
3.70
1.6
49.6
0
0.01
1.89
1.6
49.6
0
0.0067
1.43
1.6
49.6
0
0.005
1.11
0.92
30
0
0.1
1.64
0.92
30
0
0.02
0.90
0.92
30
0
0.01
0.58
0.92
30
0.6
0.1
1.33
0.92
30
0.6
0.033
0.80
0.92
30
0.6
0.02
0.57
Determine the Michaelis–Menten constant for the reaction with no inhibitor present at 30°C and at 49.6°C.
Determine the maximum velocity of the uninhibited reaction at 30°C and an enzyme concentration of 1.6 g/l.
Determine the KI for the inhibitor at 30°C and decide what type of inhibitor is being used.
3.11. An enzyme ATPase has a molecular weight of 5 × 104 daltons, a KM value of 10–4 M, and a k2 value of k2 = 104 molecules ATP/min molecule enzyme at 37°C. The reaction catalyzed is the following:
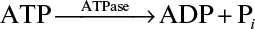
This can also be represented as
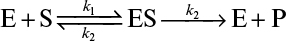
Here S is ATP. The enzyme at this temperature is unstable. The enzyme inactivation kinetics are first order:
E = E0e-kdt
Here is the initial enzyme concentration and In an experiment with a partially pure enzyme preparation, of total crude protein (containing enzyme) is added to a 1 ml reaction mixture containing 0.02 M ATP and incubated at 37°C. After 12 hours, the reaction ends (i.e., t → ∞) and the inorganic phosphate (Pi) concentration is found to be 0.002 M, which was initially zero. What fraction of the crude protein preparation was the enzyme? Hint: Since >> Km, the reaction rate can be represented by
3.12. Assume that for an enzyme immobilized on the surface of a nonporous support material, the external mass-transfer resistance for substrate is not negligible as compared to the reaction rate. The enzyme is subject to substrate inhibition (equation 3.34).
Are multiple states possible? Why or why not?
Could the effectiveness factor be greater than one?
3.13. The following data were obtained for an enzyme–catalyzed reaction. Determine Vmax and Km by inspection. Plot the data using the Eadie–Hofstee method and determine these constants graphically. Explain the discrepancy in your two determinations. The initial rate data for the enzyme–catalyzed reaction are as follows:
[S] mol/l
v μmol/min
5.0×10−4
125
2.0×10−4
125
6.0×10−5
121
4.0×10−5
111
3.0×10−5
96.5
2.0×10−5
62.5
1.6×10−5
42.7
1.0×10−5
13.9
8.0×10−6
7.50
Do these data fit into Michaelis–Menten kinetics? If not, what kind of rate expression would you suggest? Use graphical methods.
3.14. H. H. Weetall and N. B. Havewala report the following data for the production of dextrose from corn starch using both soluble and immobilized (azo-glass beads) glucoamylase in a fully agitated continuous stirred-tank reactor system:
Soluble data: T = 60°C,[S0] = 168 mg starch/ml, [E0] = 11,600 units, volume 1000 ml
Immobilized data: T = 60°C,[S0] = 336 mg starch/ml, [E0] = 46,400 units initially, immobilized, volume 1000 ml
Product concentration
(mg dextrose/ml)Time (min)
Soluble
Immobilized
0
12.0
18.4
15
40.0
135
30
76.5
200
45
94.3
236
60
120.0
260
75
135.5
258
90
151.2
262
105
150.4
266
120
155.7
278
135
160.1
300
150
164.9
310
165
170.0
306
225
—
316
415
—
320
Determine the maximum reaction velocity, (mg/ml-min unit of enzyme) and the saturation constant,
The same authors studied the effect of temperature on the maximum rate of the hydrolysis of corn starch by glucoamylase. The results are tabulated next:
Vmax (m mol/min 106)
T, °C
Soluble
Azo-immobilized
25
0.62
0.80
35
1.42
1.40
45
3.60
3.00
55
8.0
6.2
65
16.0
11.0
Determine the activation energy (∆E kcal/g-mol) for the soluble and immobilized enzyme reaction.
Using these results, determine if immobilized enzyme is diffusion limited.
(Courtesy of A. E. Humphrey from “Collected Coursework Problems in Biochemical Engineering” compiled by H. W. Blanch for 1977 American Society for Engineering Education Summer School. © American Society for Engineering Education.)
3.15. Michaelis–Menten kinetics are used to describe intracellular reactions. Yet [E0 ≈ [S0]. In in vitro batch reactors, the quasi-steady-state hypothesis does not hold for [E0 ≈ [S0]. The rapid equilibrium assumption also will not hold. Explain why Michaelis–Menten kinetics and the quasi-steady-state approximation are still reasonable descriptions of intracellular enzyme reactions.
3.16. You are working for company A and you join a research group working on immobilized enzymes. Harry, the head of the lab, claims that immobilization improves the stability of the enzyme. His proof is that the enzyme has a half-life of 10 days in free solution, but under identical conditions of temperature, pH, and medium composition, the measured half-life of a packed column is 30 days. The enzyme is immobilized in a porous sphere 5 mm in diameter. Is Harry’s reasoning right? Do you agree with him? Why or why not?
3.17. The following data were obtained from enzymatic oxidation of phenol by phenol oxidase at different phenol concentrations:
S (mg/l)
10
20
30
50
60
80
90
110
130
140
150
v (mg/l-h)
5
7.5
10
12.5
13.7
15
15
12.5
9.5
7.5
5.7
What type of inhibition is this?
Determine the constants Vm, Km, and Ksi.
Determine the oxidation rate at [S] = 70 mg/1.
3.18. Uric acid is degraded by uricase enzyme immobilized in porous Ca-alginate beads. Experiments conducted with different bead sizes result in the following rate data:
Bead diameter, Dp (cm)
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
Rate, v (mg/l.h)
200
198
180
140
100
70
50
30
Determine the effectiveness factor for particle sizes Dp = 0.5 cm and Dp = 0.7 cm.
The following data were obtained for Dp = 0.5 cm at different bulk uric acid concentrations. Assuming negligible liquid film resistance, calculate Vm and Ks for the enzyme. Assume no substrate or product inhibition.
S0 (mg UA/l)
10
25
50
100
200
250
v (mg UA/l-h)
10
20
30
40
45
46
3.19. The enzyme urease is immobilized in Ca-alginate beads 2 mm in diameter. When the urea concentration in the bulk liquid is 0.5 mM, the rate of urea hydrolysis is v = 10 mmol/l-h. Diffusivity of urea in Ca-alginate beads is De = 1.5 × 10–5 cm2/sec, and the Michaelis constant for the enzyme is
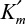= 0.2 mM. By neglecting the liquid film resistance on the beads (i.e., [So] = [Ss]) determine the following:Maximum rate of hydrolysis Vm, Thiele modulus (φ), and effectiveness factor (η)
The Vm, φ, and η values for a particle size of Dp = 4 mm.
Hint: Assume η = 3/φ for large values of φ(φ>2);
3.20. Decarboxylation of glyoxalate (S) by mitochondria is inhibited by malonate (I). The following data was obtained in batch experiments:
Rate of CO2 Evolution, v (mmoles/l-h)
Glyox,S (mM)
I = 0
I = 1.26 mM
I = 1.95 mM
0.25
1.02
0.73
0.56
0.33
1.39
0.87
0.75
0.40
1.67
1.09
0.85
0.50
1.89
1.30
1.00
0.60
2.08
1.41
1.28
0.75
2.44
1.82
1.39
1.00
2.50
2.17
1.82
What type of inhibition is this?
Determine the constants Vm,
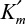, and KI.
3.21. Urea dissolved in aqueous solution is degraded to ammonia and CO2 by the enzyme urease immobilized on surfaces of nonporous polymeric beads. Conversion rate is controlled by transfer of urea to the surface of the beads through liquid film, and the conversion takes place on the surfaces of the beads. The following parameters are given for the system:
kL = 0.2 cm/s; Km = 200 mg/l
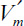= 0.1 mg urea/cm2 support surface -s.Sb = 1000 mg urea/l
Determine the surface concentration of urea.
Determine the rate of urea degradation under mass-transfer-controlled conditions.
3.22. Two enzymes are immobilized on the same flat, nonporous surface. For enzyme A, the substrate is S1. For enzyme B, the substrate is S2. The product of the first reaction is S2:
Figure 3.P1 depicts the rate of the first reaction on the surface as a function of local concentrations of S1. If the bulk concentration of S1 is 100 mg/l and the mass-transfer coefficient is 4 × 10–5 cm/s, what is the rate of consumption of for a 1 cm2 surface? What is the surface concentration of S1?
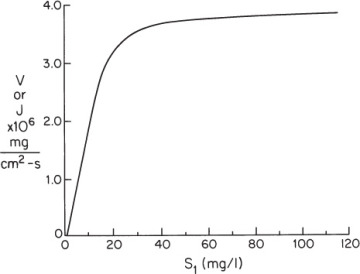
Figure 3P.1. Reaction rate data for problem 3.22. Reaction rate dependence on substrate 1 for reaction catalyzed by EA.
The rate of the second reaction follows:
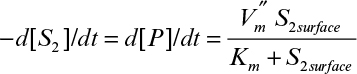
Here Km = 5 mg/1 (or 5 × 10–3 mg/cm3) and
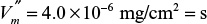. The bulk concentration of S2 [S2bulk] is maintained as 5 mg/l, and the mass-transfer coefficient is the same for S1 and S2. Calculate [S2surface] and the rate of formation of P (assuming all stoichiometric coefficients are one).3.23. Consider the case of two enzymes immobilized on the same nonporous, planar surface. S is a substrate used by both enzymes in the following reactions:
The final product P3 is formed by the spontaneous reaction of P1 and P2:
Reactions 1 and 2 occur only at the surface, and reaction 3 is a homogeneous reaction occurring throughout the bulk liquid phase.
Figure 3.P2 gives the predicted reaction-rate dependence of reaction 1 (bottom curve) alone and reaction 2 (top curve) alone based on the measured amount of each enzyme immobilized and assuming the intrinsic reaction kinetics are not altered in the process of immobilization.
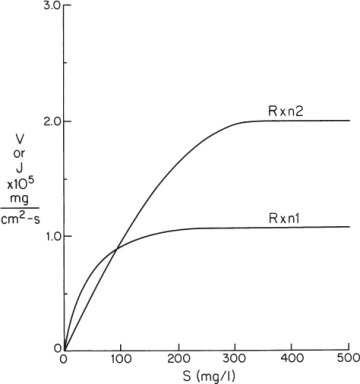
Figure 3P.2. Reaction rate data for problem 3.23. The reaction rate data for two different enzymes (E1 and E2) are shown.
If kL = 6×10–5 cm/s and the bulk concentration of substrate is 500 mg/l, what is the total rate of substrate disappearance?
What is the overall effectiveness factor under the conditions of part a?
What will be the ratio of P2 to P1 under the conditions of part a?
If you want to produce equimolar amounts of P1 and P2 and if kL = 6 × 10–5 cm/s, what value of bulk substrate concentration must you pick?
)
)
)
)
)
)