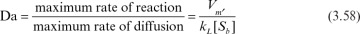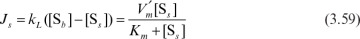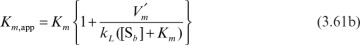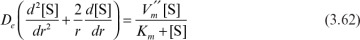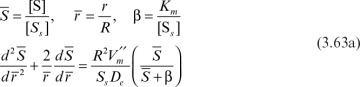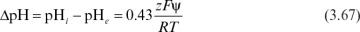This chapter is from the book
This chapter is from the book
This chapter is from the book
3.3. Immobilized Enzyme Systems
The restriction of enzyme mobility in a fixed space is known as enzyme immobilization. Immobilization of enzymes provides important advantages, such as enzyme reutilization and elimination of enzyme recovery and purification processes and may provide a better environment for enzyme activity. Because enzymes are expensive, catalyst reuse is critical for many processes. Since some of the intracellular enzymes are membrane bound, immobilized enzymes provide a model system to mimic and understand the action of some membrane-bound intracellular enzymes. Product purity is usually improved, and effluent-handling problems are minimized by immobilization.
3.3.1. Methods of Immobilization
Major methods of immobilization are summarized in Figure 3.17. The two major categories are entrapment and surface immobilization.
)
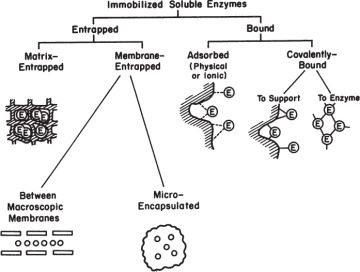
Figure 3.17. Major immobilization methods.
3.3.1.1. Entrapment
Entrapment is the physical enclosure of enzymes in a small space. Matrix entrapment and membrane entrapment, including microencapsulation, are the two major methods of entrapment.
Matrices used for enzyme immobilization are usually polymeric materials such as calcium-alginate, agar, k-carrageenin, polyacrylamide, and collagen. However, some solid matrices, such as activated carbon, porous ceramic, and diatomaceous earth, can also be used for this purpose. The matrix can be a particle, a membrane, or a fiber. When immobilizing in a polymer matrix, enzyme solution is mixed with polymer solution before polymerization takes place. Polymerized gel-containing enzyme can be extruded, or else a template is used to shape the particles from a liquid polymer–enzyme mixture. Entrapment and surface attachment may be used in combination in some cases.
Membrane entrapment of enzymes is possible; for example, hollow fiber units have been used to entrap an enzyme solution between thin, semipermeable membranes. Membranes of nylon, cellulose, polysulfone, and polyacrylate are commonly used. Configurations, other than hollow fibers, are possible, but in all cases a semipermeable membrane is used to retain high-molecular-weight compounds (enzyme) while allowing small-molecular-weight compounds (substrate or products) access to the enzyme.
A special form of membrane entrapment is microencapsulation. In this technique, microscopic hollow spheres are formed. The spheres contain the enzyme solution, and the spheres are enclosed within a porous membrane. The membrane can be polymeric or an enriched interfacial phase formed around a microdrop.
Despite the aforementioned advantages, enzyme entrapment may have its inherent problems, such as enzyme leakage into solution, significant diffusional limitations, reduced enzyme activity and stability, and lack of control of microenvironmental conditions. Enzyme leakage can be overcome by reducing the molecular weight cutoff of membranes or the pore size of solid matrices. Diffusion limitations can be eliminated by reducing the particle size of matrices and/or capsules. Reduced enzyme activity and stability are due to unfavorable microenvironmental conditions, which are difficult to control. However, by using different matrices and chemical ingredients, by changing processing conditions, and by reducing particle or capsule size, more favorable microenvironmental conditions can be obtained. Diffusion barrier is usually less significant in microcapsules as compared to gel beads.
3.3.1.2. Surface immobilization
The two major types of immobilization of enzymes on the surfaces of support materials are adsorption and covalent binding.
Adsorption is the attachment of enzymes on the surfaces of support particles by weak physical forces, such as van der Waals or dispersion forces. The active site of the adsorbed enzyme is usually unaffected, and nearly full activity is retained upon adsorption. However, desorption of enzymes is a common problem, especially in the presence of strong hydrodynamic forces, because binding forces are weak. Adsorption of enzymes may be stabilized by cross-linking with glutaraldehyde. Glutaraldehyde treatment can denature some proteins. Support materials used for enzyme adsorption can be inorganic materials, such as alumina, silica, porous glass, ceramics, diatomaceous earth, clay, and bentonite, or organic materials, such as cellulose (CMC, DEAE-cellulose), starch, activated carbon, and ion-exchange resins, such as Amberlite, Sephadex, and Dowex. The surfaces of the support materials may need to be pretreated (chemically or physically) for effective immobilization.
Covalent binding is the retention of enzymes on support surfaces by covalent bond formation. Enzyme molecules bind to support material via certain functional groups, such as amino, carboxyl, hydroxyl, and sulfhydryl groups. These functional groups must not be in the active site. One common trick is to block the active site by flooding the enzyme solution with a competitive inhibitor prior to covalent binding. Functional groups on support material are usually activated by using chemical reagents, such as cyanogen bromide, carbodiimide, and glutaraldehyde. Support materials with various functional groups and the chemical reagents used for the covalent binding of proteins are listed in Table 3.3. Binding groups on the protein molecule are usually side groups (R) or the amino or carboxyl groups of the polypeptide chain.
)
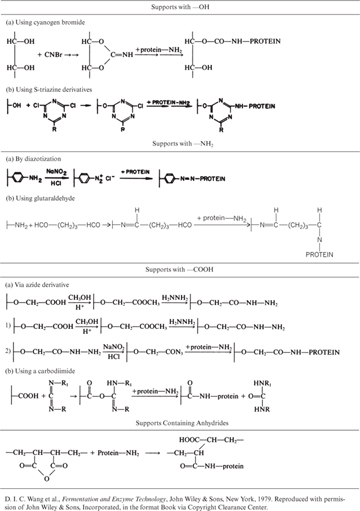
Table 3.3. Methods of Covalent Binding of Enzymes to Supports
The cross-linking of enzyme molecules using agents such as glutaraldehyde, bis-diazobenzidine, and 2,2-disulfonic acid is another method of enzyme immobilization. Cross-linking can be achieved in several ways: enzymes can be cross-linked with glutaraldehyde to form an insoluble aggregate, adsorbed enzymes may be cross-linked, or cross-linking may take place following the impregnation of porous support material with enzyme solution. Cross-linking may cause significant changes in the active site of enzymes, and severe diffusion limitations may result.
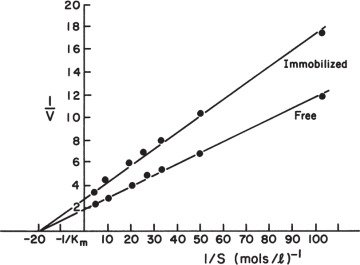
The most suitable support material and immobilization method vary depending on the enzyme and particular application. Two major criteria used in the selection of support material are the binding capacity of the support material, which is a function of charge density, functional groups, porosity, and hydrophobicity of the support surface; and stability and retention of enzymatic activity, which is a function of functional groups on support material and microenvironmental conditions. If immobilization causes some conformational changes on the enzyme, or if reactive groups on the active site of the enzyme are involved in binding, a loss in enzyme activity can take place upon immobilization. Usually, immobilization results in a loss in enzyme activity and stability. However, in some cases, immobilization may cause an increase in enzyme activity and stability due to more favorable microenvironmental conditions. Because enzymes often have more than one functional site that can bind the surface, an immobilized enzyme preparation may be very heterogeneous. Even when binding does not alter enzyme structure, some enzyme can be bound with the active site oriented away from the substrate solution and toward the support surface, decreasing the access of the substrate to the enzyme. Retention of activity varies with the method used. Table 3.4 summarizes the retention of activity of aminoacylase immobilized by different methods.
Table 3.4. Immobilization Effects on Enzymatic Activity of Aminoacylase
Support |
Method |
Observed Activity (units) |
Enzyme Activity Immobilized (%) |
Polyacrylamide |
Entrapment |
526 |
52.6 |
Nylon |
Encapsulation |
360 |
36.0 |
DEAE-cellulose |
Ionic binding |
668 |
55.2 |
DEAE-Sephadex A-5O |
Ionic binding |
680 |
56.2 |
CM-Sephadex C-5O |
Ionic binding |
0 |
0 |
Iodoacetyl cellulose |
Covalent binding |
472 |
39.0 |
CNBr-activated Sephadex |
Covalent binding |
12 |
1.0 |
AE-cellulose |
Cross-linked with glutaraldehyde |
8 |
0.6 |
D. I. C. Wang et al., Fermentation and Enzyme Technology, John Wiley & Sons, New York, 1979. Reproduced with permission of John Wiley & Sons, Incorporated, in the format Book via Copyright Clearance Center.
3.3.2. Diffusional Limitations in Immobilized Enzyme Systems
Diffusional resistances may be observed at different levels in immobilized enzymes. These resistances vary depending on the nature of the support material (porous, nonporous), hydrodynamical conditions surrounding the support material, and distribution of the enzyme inside or on the surface of the support material. Whether diffusion resistance has a significant effect on the rate of enzymatic reaction rate depends on the relative rate of the reaction rate and diffusion rate, which is characterized by the Damköhler number (Da):
)
where [Sb] is substrate concentration in bulk liquid, and kL is the mass-transfer coefficient.
The rate of enzymatic conversion may be limited by diffusion of the substrate or reaction, depending on the value of the Damköhler number. If Da >> 1, then the diffusion rate is limiting. For Da << 1, the reaction rate is limiting, and for Da ≈ 1, the diffusion and reaction resistances are comparable. Diffusion and enzymatic reactions may be simultaneous, with enzymes entrapped in a solid matrix, or may be two consecutive phenomena for adsorbed enzymes.
3.3.2.1. Diffusion effects on surface-bound enzymes
Assume a situation where enzymes are bound and evenly distributed on the surface of a nonporous support material, all enzyme molecules are equally active, and substrate diffuses through a thin liquid film surrounding the support surface to reach the reactive surfaces, as depicted in Figure 3.18. Assume further that the process of immobilization has not altered the protein structure, and the intrinsic kinetic parameters (Vm, Km) are unaltered.
)
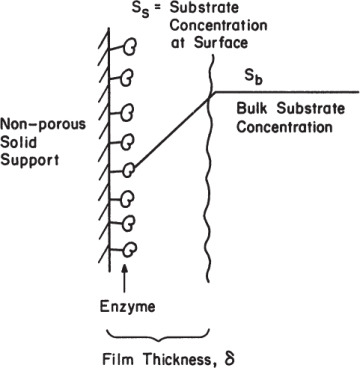
Figure 3.18. Substrate concentration profile in a liquid film around adsorbed enzymes.
At steady state, the reaction rate is equal to the mass-transfer rate:
)
where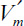 
is the maximum reaction rate per unit of external surface area, and kL is the liquid mass-transfer coefficient. This equation is quadratic in [Ss], the substrate concentration at the surface. It can be solved analytically, but the solution is cumbersome. Furthermore, the value of [Ss] is not amenable to direct experimental observation.
Equation 3.59 can be solved graphically, as depicted in Figure 3.19. Such a plot also makes it easy to visualize the effects of parameter changes such as in stirring rate, bulk substrate concentration, or enzyme loading.
)
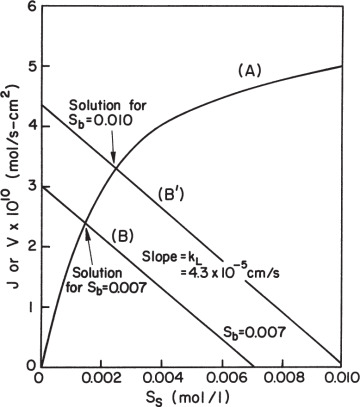
Figure 3.19. Graphical solution for amount of reaction per unit surface area for enzyme immobilized on a nonporous catalyst. Curve A results from the intrinsic solution-based kinetic parameters and the surface loading of enzyme. Line B is the mass-transfer equation. The intersection of the two lines is the reaction rate that can be sustained in the system. The responses for two different bulk substrate concentrations are shown.
When the system is strongly mass-transfer limited, [Ss] ≈ 0, since the reaction is rapid compared to mass transfer. As a result, the system behaves as a pseudo-first-order reaction:
)
When the system is reaction limited (Da << 1), the reaction rate is often expressed as
)
where, with appropriate assumptions,
)
Under these circumstances, the apparent Michaelis–Menten constant is a function of stirring speed. Usually, Km,app is estimated experimentally as the value of [Sb], giving one-half of the maximal reaction rate.
3.3.2.2. Diffusion effects in enzymes immobilized in a porous matrix
When enzymes are immobilized on internal pore surfaces of a porous matrix, substrate diffuses through the tortuous pathway among pores and reacts with enzyme immobilized on pore surfaces. Diffusion and reaction are simultaneous in this case, as depicted in Figure 3.20.
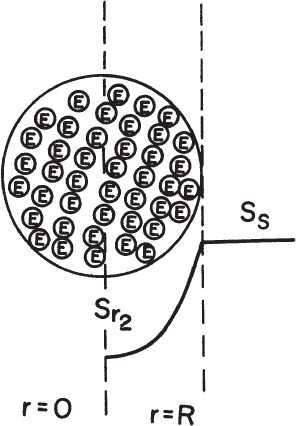
Figure 3.20. Substrate concentration profile in a porous support particle containing immobilized enzymes. Here it is assumed that no external substrate limitation exists so that the bulk and surface concentrations are the same.
Assume that the enzyme is uniformly distributed in a spherical support particle; the reaction kinetics are expressed by Michaelis–Menten kinetics, and there is no partitioning of the substrate between the exterior and interior of the support. Then we write the following equation, stating that diffusion rate is equal to reaction rate at steady state:
)
Boundary conditions are [S] = [Ss] at r = R and d[S]/dr = 0 at r = 0, where 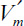is the maximum reaction rate per unit volume of support, and De is the effective diffusivity of substrate within the porous matrix.
Equation 3.62 can be written in dimensionless form by defining the following dimensionless variables:
)
or
)
where
)
With boundary conditions of 
at 
and 
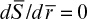at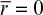 
Equation 3.63b can be numerically solved to determine the substrate profile inside the matrix. The rate of substrate consumption is equal to the rate of substrate transfer through the external surface of the support particle at steady state into the sphere:
)
Under diffusion limitations, the rate per unit volume is usually expressed in terms of the effectiveness factor:
)
The effectiveness factor is defined as the ratio of the reaction rate with diffusion limitation (or diffusion rate) to the reaction rate with no diffusion limitation. The value of the effectiveness factor is a measure of the extent of diffusion limitation. For η < 1, the conversion is diffusion limited, whereas for η ≈ 1 values, conversion is limited by the reaction rate and diffusion limitations are negligible. The factor is a function of φ and β, as depicted in Figure 3.21.
)
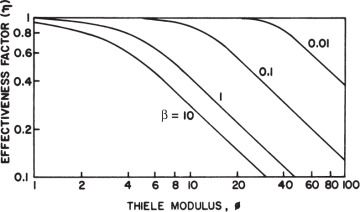
Figure 3.21. Theoretical relationship between the effectiveness factor and first-order Thiele modulus. (D. I. C. Wang et al., Fermentation and Enzyme Technology, John Wiley & Sons, New York, 1979. Reproduced with permission of John Wiley & Sons, Incorporated, in the format Book via Copyright Clearance Center.)
For a zero-order reaction rate (β → 0), and consequently η ≈ 1 for a large range of Thiele modulus values such as 1 < φ < 100. For a first-order reaction rate (β → ∞), η = (φ,β) and h is approximated to the following equation for high values of φ:
)
When internal diffusion limits the enzymatic reaction rate, the rate-constant Vm,app and Km,app values are not true intrinsic rate constants but apparent values. To obtain true intrinsic rate constants in immobilized enzymes, diffusion resistances should be eliminated by using small particle sizes, a high degree of turbulence around the particles, and high substrate concentrations.
When designing immobilized enzyme systems using a particular support, the main variables are Vm and R, since the substrate concentration, Km, and De are fixed. The particle size (R) should be as small as possible within the constraints of particle integrity, resistance to compression, and the nature of the particle recovery systems. The maximum reaction rate is determined by enzyme activity and concentration in the support. High enzyme content will result in high enzyme activity per unit of reaction volume but low effectiveness factor. Low enzyme content will result in lower enzyme activity per unit volume but a high effectiveness factor. For maximum conversion rates, particle size should be small (Dp ≤ 10 μm) and enzyme loading should be optimized. As depicted in the example in Figure 3.22, Dp ≤ 10 μm and enzyme loadings of less than 10 mg/cm3 are required for high values of the effectiveness factor (η ≥ 0.8).
)
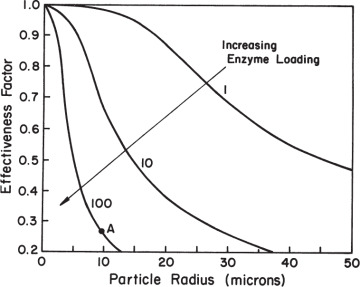
Figure 3.22. The effectiveness factor decreases with increases in enzyme loading or with increases in particle diameter. Point A represents the value of the effectiveness factor for a particle radius of 10 μm with an enzyme loading of 100 mg/cm3, an enzyme activity of 100 μmol/min per mg enzyme, a substrate diffusivity of 5 × 10–6 cm2/s, and a bulk substrate concentration tenfold higher than Km.
Example 3.5 Determining Whether Diffusional Limitations Exist
D. Thornton and coworkers studied the hydrolysis of sucrose at pH = 4.5 and 25°C using crude invertase obtained from baker’s yeast in free and immobilized form. The following initial velocity data were obtained with 408 units of crude enzyme (1 unit = quantity of enzyme hydrolyzing 1 μmol of sucrose/min when incubated with 0.29 M sucrose in a buffer at pH 4.5 and 25°C).
V0 (mmol hydrolyzed/l-min) |
|
|
Free Enzyme |
Immobilized Enzyme |
S0 (mol/l) |
0.083 |
0.056 |
0.010 |
0.143 |
0.098 |
0.020 |
0.188 |
0.127 |
0.030 |
0.222 |
0.149 |
0.040 |
0.250 |
0.168 |
0.050 |
0.330 |
0.227 |
0.100 |
0.408 |
0.290 |
0.290 |
Determine the Km and Vm for this reaction using both free and immobilized enzyme.
Do the data indicate any diffusion limitations in the immobilized enzyme preparation?
Solution
From a double-reciprocal plot of 1/v versus 1/S for free enzyme (Figure 3.23), –1/Km = –20 and Km = 0.05 M. 1/Vm = 2 and Vm = 0.5 mmol/l-min. From a double-reciprocal plot of 1/v versus 1/S for the immobilized enzyme, –1/Km = –20 and Km = 0.05 M. 1/Vm = 3 and Vm = 0.33 mmol/l-min. Since the Km values for free and immobilized enzymes are the same, there is no diffusion limitation.
)
Figure 3.23. Double-reciprocal plots for free and immobilized enzymes (Example 3.5).
3.3.3. Electrostatic and Steric Effects in Immobilized Enzyme Systems
When enzymes are immobilized in a charged matrix as a result of a change in the microenvironment of the enzyme, the apparent bulk pH optimum of the immobilized enzyme will shift from that of soluble enzyme. The charged matrix will repel or attract substrates, product, cofactors, and H+ depending on the type and quantity of surface charge. For an enzyme immobilized onto a charged support, the shift in the pH-activity profile is given by
)
){kind=link}
where pHi and pHe are internal and external pH values, respectively; z is the charge (valence) on the substrate; F is the Faraday constant (96,500 coulomb/mol); ψ is the electrostatic potential; and R is the gas constant. Expressions similar to equation 3.67 apply to other nonreactive charged medium components. The intrinsic activity of the enzyme is altered by the local changes in pH and ionic constituents. Further alterations in the apparent kinetics are due to the repulsion or attraction of substrates or inhibitors.
The activity of an enzyme toward a high-molecular-weight substrate is usually reduced upon immobilization to a much greater extent than for a low-molecular-weight substrate, mainly because of steric hindrance by the support. Certain substrates, such as starch, have molecular weights comparable to those of enzymes and may therefore not be able to penetrate to the active sites of immobilized enzymes.
Immobilization also affects the thermal stability of enzymes. Thermal stability often increases upon immobilization due to the presence of thermal diffusion barriers and the constraints on protein unfolding. However, decreases in thermal stability have been noted in a few cases. The pH stability of enzymes may also increase upon immobilization.