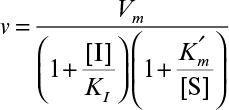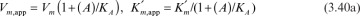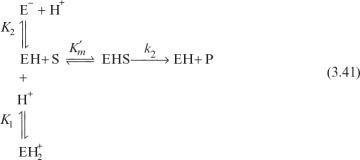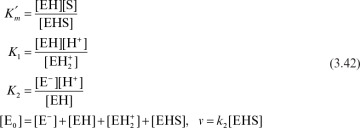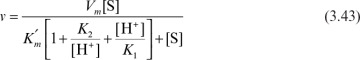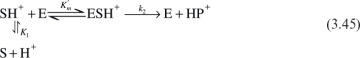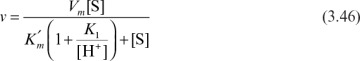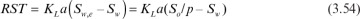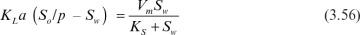3.2. Enzyme Kinetics
A mathematical model of the kinetics of single-substrate-enzyme-catalyzed reactions was first developed by V. C. R. Henri in 1902 and by L. Michaelis and M. L. Menten in 1913. Kinetics of simple enzyme–catalyzed reactions are often referred to as Michaelis–Menten kinetics or saturation kinetics. The qualitative features of enzyme kinetics are similar to Langmuir–Hinshelwood kinetics (see Figure 3.3). These models are based on data from batch reactors with constant liquid volume in which the initial substrate, [S0], and enzyme, [E0], concentrations are known. More complicated enzyme–substrate interactions such as multisubstrate–multienzyme reactions can take place in biological systems.
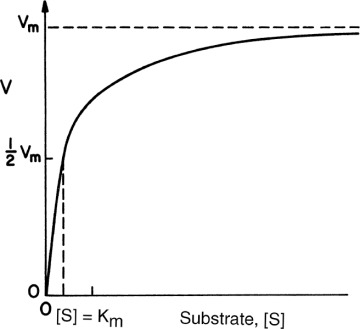
Figure 3.3. Effect of substrate concentration on the rate of an enzyme–catalyzed reaction.
An enzyme solution has a fixed number of active sites to which substrates can bind. At high substrate concentrations, all these sites may be occupied by substrates, or the enzyme is saturated. Saturation kinetics can be obtained from a simple reaction scheme that involves a reversible step for enzyme–substrate complex formation and a dissociation step of the enzyme–substrate complex:
It is assumed that the enzyme–substrate complex is established rather rapidly and the rate of the reverse reaction of the second step is negligible. The assumption of an irreversible second reaction often holds only when product accumulation is negligible at the beginning of the reaction. Two major approaches used in developing a rate expression for the enzyme–catalyzed reactions are rapid-equilibrium approach and quasi-steady-state approach.
3.2.1. Mechanistic Models for Simple Enzyme Kinetics
Both the quasi-steady-state approximation and the assumption of rapid equilibrium share the same few initial steps in deriving a rate expression for the mechanism in equation 3.1, where the rate of product formation is
where v is the rate of product formation or substrate consumption in mol/l-s.
The rate constant k2 is often denoted as kcat in the biological literature. The rate of variation of the enzyme–substrate complex is
Since the enzyme is not consumed, the conservation equation on the enzyme yields
At this point, an assumption is required to achieve an analytical solution.
3.2.1.1. The rapid-equilibrium assumption
Henri, Michaelis, and Menten used essentially this approach. Assuming a rapid equilibrium between the enzyme and substrate to form an [ES] complex, we can use the equilibrium coefficient to express [ES] in terms of [S].
The equilibrium constant is
Since [E] = [E0] – [ES], if enzyme is conserved, then
where 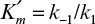 , which is the dissociation constant of the enzyme–substrate complex. Substituting equation 3.7 into equation 3.2 yields
, which is the dissociation constant of the enzyme–substrate complex. Substituting equation 3.7 into equation 3.2 yields
where Vm = k2[E0].
In this case, the maximum forward velocity of the reaction is Vm. Vm changes if more enzyme is added, but the addition of more substrate has no influence on Vm. 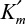 is often called the Michaelis–Menten constant, and the prime reminds us that it was derived by assuming rapid equilibrium in the first step. A low value of
is often called the Michaelis–Menten constant, and the prime reminds us that it was derived by assuming rapid equilibrium in the first step. A low value of 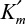 suggests that the enzyme has a high affinity for the substrate. Also,
suggests that the enzyme has a high affinity for the substrate. Also, 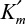 corresponds to the substrate concentration, giving the half-maximal reaction velocity.
corresponds to the substrate concentration, giving the half-maximal reaction velocity.
An equation of exactly the same form as equation 3.8 can be derived with a different, more general assumption applied to the reaction scheme in equation 3.1.
3.2.1.2. The quasi-steady-state assumption
In many cases, the assumption of rapid equilibrium following mass-action kinetics is not valid, although the enzyme–substrate reaction still shows saturation-type kinetics.
G. E. Briggs and J. B. S. Haldane first proposed using the quasi-steady-state assumption. In most experimental systems, a closed system (batch reactor) is used in which the initial substrate concentration greatly exceeds the initial enzyme concentration. They suggest that since [E0] was small, d[ES]/dt ≈ 0. (This logic is flawed. Do you see why?) Computer simulations of the actual time course represented by equations 3.2, 3.3, and 3.4 have shown that in a closed system, the quasi-steady-state hypothesis holds after a brief transient if[S0] >> [E0] (e.g., 100×). Figure 3.4 displays one such time course.
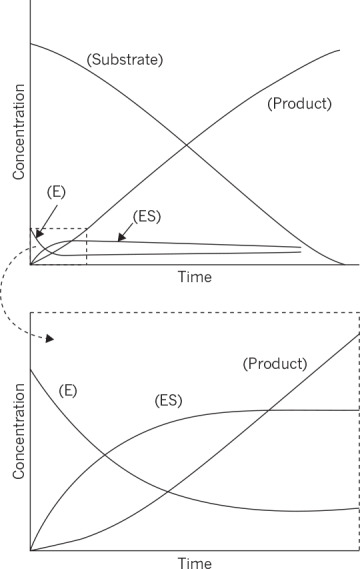
Figure 3.4. Time course of the formation of an enzyme–substrate complex and initiation of the steady state, as derived from computer solutions of data obtained in an actual experiment on a typical enzyme. The portion in the dashed box in the top graph is shown in magnified form on the lower graph. (From Lehninger, Principles of Biochemistry, 6th ed., by David L. Nelson et al., Copyright 2013. All rights reserved. Reprinted by permission of W. H. Freeman.)
By applying the quasi-steady-state assumption to equation 3.3, we find
Substituting the enzyme conservation equation 3.4 in equation 3.9 yields
Solving equation 3.10 for [ES],
Substituting equation 3.11 into equation 3.2 yields
where Km is (k–1 + k2)/k1 and Vm is k2[E0]. Under most circumstances (simple experiments), it is impossible to determine whether Km or 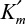 is more suitable. Since Km results from the more general derivation, we use it in the rest of our discussions.
is more suitable. Since Km results from the more general derivation, we use it in the rest of our discussions.
3.2.2. Determining Rate Parameters for Michaelis–Menten Kinetics
The determination of values for Km and Vm with high precision may be difficult. Typically, experimental data are obtained from initial-rate experiments. A batch reactor is charged with a known amount of substrate [S0] and enzyme [E0]. The product (or substrate concentration) is plotted against time. The initial slope of this curve is estimated (i.e., v = d[P]/dt|t=0 = d[S]/dt|t=0). This value of v then depends on the values of [E0] and [S0] in the charge to the reactor. Many such experiments at different initial substrate concentrations can be performed to generate many pairs of v0 and [S]0 data. The initial rate data at different [S]0 levels could be plotted as in Figure 3.3; however, the accurate determination of Km from such a plot is very difficult. Consequently, other methods of analyzing such data have been suggested.
3.2.2.1. Double-reciprocal plot (Lineweaver–Burk plot)
Equation 3.12b can be linearized in double-reciprocal form:
A plot of 1/v versus 1/[S] yields a linear line with a slope of Km/Vm and y-axis intercept of 1/Vm, as depicted in Figure 3.5. A double-reciprocal plot gives good estimates on Vm but not necessarily on Km. Because the error about the reciprocal of a data point is not symmetric, be cautious in applying regression analysis (least squares) to such plots. Data points at low substrate concentrations influence the slope and intercept more than those at high substrate concentrations.
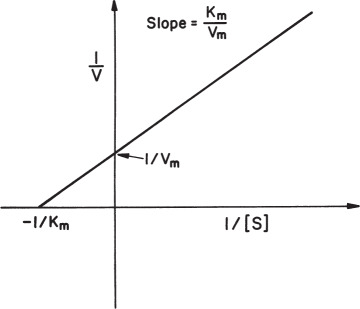
Figure 3.5. Double-reciprocal (Lineweaver–Burk) plot.
3.2.2.2. Eadie–Hofstee plot
Equation 3.12b can be rearranged as
A plot of v versus v/[S] results in a line of slope –Km and y-axis intercept of Vm, as depicted in Figure 3.6. Eadie–Hofstee plots can be subject to large errors because both coordinates contain υ, but there is less bias on points at low [S]. This is a good method for estimation of Km but not Vm.
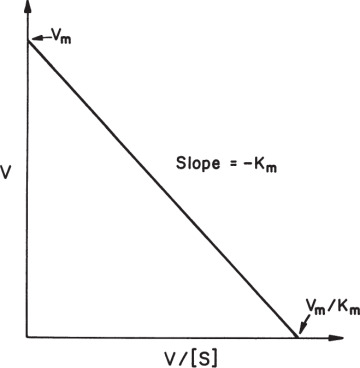
Figure 3.6. Eadie–Hofstee plot.
3.2.2.3. Hanes–Woolf plot
Rearrangement of Equation 3.12b yields
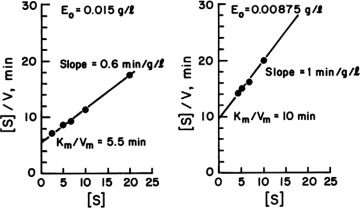
A plot of [S]/v versus [S] results in a line of slope 1/Vm and y-axis intercept of Km/Vm, as depicted in Figure 3.7. This plot is used to determine Vm more accurately.
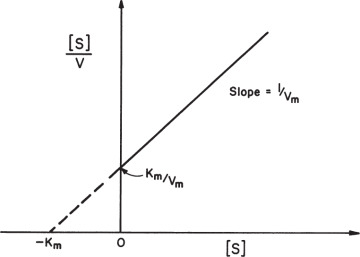
Figure 3.7. Hanes–Woolf plot.
It is preferable to determine kinetic constants from any of these approaches based on the slope rather than the intercept. The intercept often designates hypothetical cases where S or V approach zero or infinity. Multivariable regression analyses are also commonly used for determination of the kinetic constants using the experimental data.
3.2.2.4. Batch kinetics
The time course of variation of [S] in a batch enzymatic reaction can be determined from
Equation 3.12b can be integrated to yield
Equation 3.16 can be rearranged to give
A plot of 1/t Ln[S0]/[S] versus {[S0] – [S]}/t results in a line of slope –1Km and intercept of Vm/Km. However, Vm may be better determined from a plot of Ln [S0]/[S] versus time (t), where the slope is Vm/Km and the intercept is {[S0] – [S]}/Km.
3.2.2.5. Interpretation of Km and Vm
While Km (or 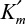 ) is an intrinsic parameter, Vm is not. Km is solely a function of rate parameters and is expected to change with temperature or pH. However, Vm is a function of the rate parameter k2 and the initial enzyme level, [E0]. As [E0] changes, so does Vm. Of course, k2 can be readily calculated if [E0] is known. For highly purified enzyme preparations, it may be possible to express [E0] in terms of mol/l or g/l.
) is an intrinsic parameter, Vm is not. Km is solely a function of rate parameters and is expected to change with temperature or pH. However, Vm is a function of the rate parameter k2 and the initial enzyme level, [E0]. As [E0] changes, so does Vm. Of course, k2 can be readily calculated if [E0] is known. For highly purified enzyme preparations, it may be possible to express [E0] in terms of mol/l or g/l.
When the enzyme is part of a crude preparation, its concentration is in terms of “units.” A unit is the amount of enzyme that gives a predetermined amount of catalytic activity under specific conditions. For example, one unit would be the formation of one μmol product per minute at a specified pH and temperature with a substrate concentration much greater than the value of Km. The specific activity is the number of units of activity per amount of total protein. For example, a crude cell lysate might have a specific activity of 0.2 units/mg protein, which upon purification may increase to 10 units/mg protein. Only enzyme that remains catalytically active will be measured. The enzyme may be denatured if it unfolds or has its three-dimensional shape altered by extreme pH or temperature changes during purification. The denatured enzyme will have no activity.
3.2.3. Models for More Complex Enzyme Kinetics
The kinetics of enzyme reactors can become quite complex. Here we discuss some examples of common kinetic expressions that involve multiple binding sites. These expressions show inhibition or activation by small molecules. These complex kinetic forms are often required within a cell to describe enzymes that regulate cellular function. For example, if too much of a product is formed, the cell may need to slow its production rate. Conversely, it may be necessary to activate an enzyme to a higher rate of conversion to respond to changes in other intracellular chemical concentrations. Some of these examples of cell regulation are given in Chapter 4, “How Cells Work.” Here we focus on the kinetics of individual isolated enzymes, often for industrial use outside of the cell. We must be aware of these kinetics to design properly processes using enzymes as industrial catalysts.
3.2.3.1. Allosteric enzymes
Some enzymes have more than one substrate-binding site. The binding of one substrate to the enzyme facilitates binding of other substrate molecules. This behavior is known as allostery or cooperative binding, and regulatory enzymes show this behavior. The rate expression in this case is
where n = cooperativity coefficient and n > 1 indicates positive cooperativity. Figure 3.8 compares Michaelis–Menten kinetics with allosteric enzyme kinetics, indicating a sigmoidal shape of υ–[S] plot for allosteric enzymes.

Figure 3.8. Comparison of Michaelis–Menten and allosteric enzyme kinetics.
The cooperativity coefficient can be determined by rearranging equation 3.18 as follows and by plotting Ln v/(Vm – v) versus Ln[S], as depicted in Figure 3.9:
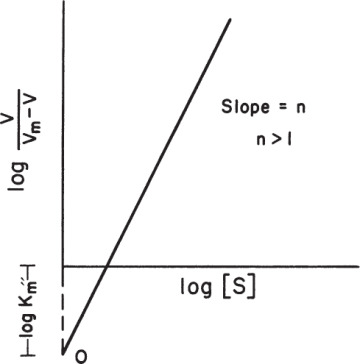
Figure 3.9. Determination of cooperativity coefficient.
Depending on the value of n, substrate binding may be cooperative when n > 1, or noncooperative (prohibitive) when n < 1. Substrate binding is independent or not affected from the other bound substrates when n = 1, which is a major assumption for Michaelis–Menten kinetics.
3.2.3.2. Inhibited enzyme kinetics
Certain compounds may bind to enzymes and reduce their activity. These compounds are known to be enzyme inhibitors. Enzyme inhibitions may be irreversible or reversible. Irreversible inhibitors such as heavy metals (lead, cadmium, mercury, and others) form a stable complex with enzyme and reduce enzyme activity. Such enzyme inhibition may be reversed only by using chelating agents such as EDTA (ethylenediaminetetraacetic acid) and citrate. Reversible inhibitors may dissociate more easily from the enzyme after binding. The three major classes of reversible enzyme inhibitions are competitive, noncompetitive, and uncompetitive inhibitions. The substrate may act as an inhibitor in some cases.
Competitive inhibitors are usually substrate analogs and compete with substrate for the active site of the enzyme. The competitive enzyme inhibition scheme can be described as
Let us assume rapid equilibrium and a definition of
We can then develop the following equation for the rate of enzymatic conversion:
or
where
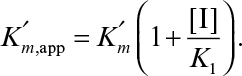
The net effect of competitive inhibition is an increased value of 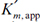 , and, therefore, reduced reaction rate. Competitive inhibition can be overcome by high concentrations of substrate. Figure 3.10 describes competitive enzyme inhibition in the form of a double-reciprocal plot.
, and, therefore, reduced reaction rate. Competitive inhibition can be overcome by high concentrations of substrate. Figure 3.10 describes competitive enzyme inhibition in the form of a double-reciprocal plot.
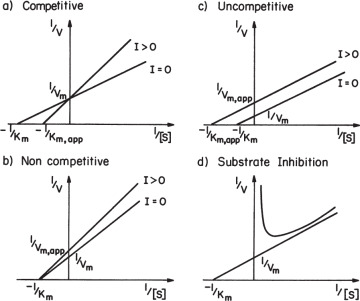
Figure 3.10. Different forms of inhibited enzyme kinetics.
Noncompetitive inhibitors are not substrate analogs. Inhibitors bind on sites other than the active site and reduce enzyme affinity to the substrate. Noncompetitive enzyme inhibition can be described as follows:
With the definitions of
we can develop the following rate equation:
or
where
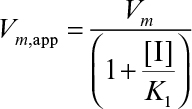
The net effect of noncompetitive inhibition is a reduction in Vm. High substrate concentrations would not overcome noncompetitive inhibition. Other reagents need to be added to block binding of the inhibitor to the enzyme. In some forms of noncompetitive inhibition Vm is reduced and 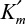 is increased. This occurs if the complex ESI can form product.
is increased. This occurs if the complex ESI can form product.
Uncompetitive inhibitors bind to the ES complex only and have no affinity for the enzyme itself. The scheme for uncompetitive inhibition follows:
With the definitions of
we can develop the following equation for the rate of reaction:
or
The net effect of uncompetitive inhibition is a reduction in both Vm and 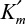 values. Reduction in Vm has a more pronounced effect than reduction in
values. Reduction in Vm has a more pronounced effect than reduction in 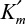 and the net result is a reduction in reaction rate. Uncompetitive inhibition is described in Figure 3.10 in the form of a double-reciprocal plot.
and the net result is a reduction in reaction rate. Uncompetitive inhibition is described in Figure 3.10 in the form of a double-reciprocal plot.
Mixed inhibition mechanism is somewhat similar to the noncompetitive enzyme inhibition with the only difference that both the maximum reaction rate (Vm) decreases and the 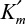 increases as follows:
increases as follows:
and
In this case, the inhibitors do not bind to the active site allowing the substrate to bind the EI complex to form ESI which has some catalytic activity to produce product.
High substrate concentrations may cause inhibition in some enzymatic reactions, known as substrate inhibition. Substrate inhibition is described in Figure 3.11.
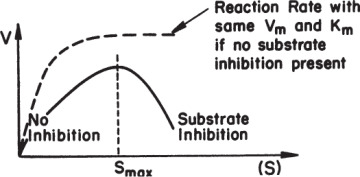
Figure 3.11. Comparison of substrate-inhibited and uninhibited enzymatic reactions.
The reaction scheme for uncompetitive substrate inhibition is
Consider the following definitions:
The assumption of rapid equilibrium yields
A double-reciprocal plot describing substrate inhibition is given in Figure 3.10.
At low substrate concentrations, [S]2/Ks1 <<1, and inhibition effect is not observed. The rate is
or
A plot of 1/v versus 1/[S] results in a line of slope 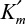 /Vm and intercept of 1/Vm.
/Vm and intercept of 1/Vm.
At high substrate concentrations, 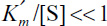 and inhibition is dominant. The rate is
and inhibition is dominant. The rate is
or
A plot of 1/v versus [S] results in a line of slope 1/KS1. Vm and intercept of 1/Vm.
The substrate concentration resulting in the maximum reaction rate can be determined by setting dv/d [S] = 0. The [S]max is given by
3.2.3.3. Enzyme activation
Just as enzyme inhibitors lower enzymatic activity, some molecules may bind to the enzymes to increase the enzymatic activity. These compounds are known as the enzyme activators, which are usually involved in allosteric enzymes for regulation of the metabolism.
A good example of an enzyme activator is fructose 2,6 biphosphate, which activates phosphofructokinase and increases the rate of metabolism in response to the hormone glucagon.
The activation energy of the enzymatic reaction is reduced upon binding the activator to the enzyme molecule increasing the reaction rate.
An activator molecule can increase the Vm or decrease the 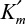 or can do both with a net effect of increasing the rate of enzymatic reaction. In the presence of an activator the enzyme kinetics may take the following form:
or can do both with a net effect of increasing the rate of enzymatic reaction. In the presence of an activator the enzyme kinetics may take the following form:
and
Here (A) is the activator concentration and KA is the dissociation constant for the enzyme–activator complex. The term (1 + (A)/KA) is known as the activation factor.
In the presence of an inhibitor 1, the activator may bind to the inhibitor molecule preventing the inhibitor to bind the enzyme and hence improving the reaction rate. In this case only the 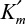 value decreases yielding higher reaction rates.
value decreases yielding higher reaction rates.
3.2.4. Effects of pH and Temperature
Enzyme activity responds directly to changes in the physical environment, such as pH and temperature. It is important to incorporate these effects into kinetic expressions for enzyme activity.
3.2.4.1. pH effects
Certain enzymes have ionic groups on their active sites, and these ionic groups must be in a suitable form (acid or base) to function. Variations in the pH of the medium result in changes in the ionic form of the active site and changes in the activity of the enzyme and hence the reaction rate. Changes in pH may also alter the three-dimensional shape of the enzyme. For these reasons, enzymes are active only over a certain pH range. The pH of the medium may affect the maximum reaction rate, Km, and the stability of the enzyme. In some cases, the substrate may contain ionic groups, and the pH of the medium affects the affinity of the substrate to the enzyme.
The following scheme may be used to describe pH dependence of the enzymatic reaction rate for ionizing enzymes:
For example, from the definition of
we can derive the following rate expression:
or
where
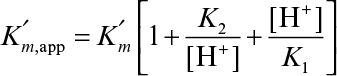
As a result of this behavior, the pH optimum of the enzyme is between pK1 and pK2.
For ionizing substrate, the following scheme and rate expression can be developed:
Theoretical prediction of the pH optimum of enzymes requires knowledge of the active site characteristics of enzymes, which is very difficult to obtain. The pH optimum for an enzyme is usually determined experimentally. Figure 3.14 depicts variation of enzymatic activity with pH for the enzymes (A) trypsin and (B) cholinesterase.
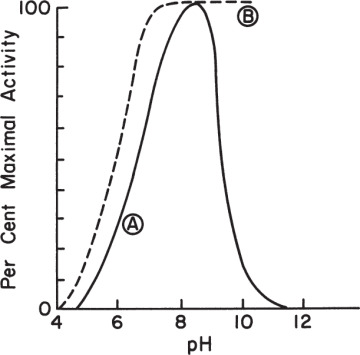
Figure 3.14. The pH-activity profiles of two enzymes. (A) approximate activity for trypsin; (B) approximate activity for cholinesterase.
3.2.4.2. Temperature effects
The rate of enzyme–catalyzed reactions increases with temperature up to a certain limit. Above a certain temperature, enzyme activity decreases with temperature because of enzyme denaturation. Figure 3.15 depicts the variation of reaction rate with temperature and the presence of an optimal temperature.
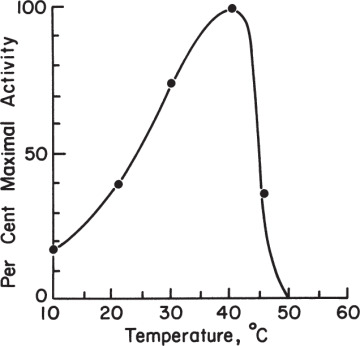
Figure 3.15. Effect of temperature on the activity of an enzyme. Here we have assumed a value of Ea = 11 kcal/g-mol and Ed = 70 kcal/g-mol. The descending portion of the curve is due to thermal denaturation and is calculated assuming a 10-min exposure to the temperature. Note that the nature of the plot will depend on the length of time the reaction mixture is exposed to the test temperature.
The ascending part of Figure 3.15 is known as temperature activation. The rate varies according to the Arrhenius equation in this region:
Here Ea is the activation energy (kcal/mol) and [E] is the active enzyme concentration. A plot of Ln υ versus 1/T results in a line of slope –Ea/R.
The descending part of Figure 3.15 is known as temperature inactivation or thermal denaturation. The kinetics of thermal denaturation can be expressed as follows:
or
Here [E0] is the initial enzyme concentration, and kd is the denaturation constant. kd also varies with temperature according to the Arrhenius equation:
Here Ed is the deactivation energy (kcal/mol). Consequently, we get the following:
The activation energies of enzyme–catalyzed reactions are within the 4 to 20 kcal/g-mol range (mostly about 11 kcal/g-mol). Deactivation energies Ed vary between 40 and 130 kcal/g-mol (mostly about 70 kcal/g-mol). That is, enzyme denaturation by temperature is much faster than enzyme activation. A rise in temperature from 30° to 40°C results in a 1.8-fold increase in enzyme activity but a 41-fold increase in enzyme denaturation. Variations in temperature may affect both Vm and Km values of enzymes.
3.2.5. Insoluble Substrates
Enzymes are often used to attack large, insoluble substrates such as wood chips (in biopulping for paper manufacture) or cellulosic residues from agriculture (e.g., cornstalks). In these cases, access to the reaction site on these biopolymers by enzymes is often limited by enzyme diffusion. The number of potential reactive sites exceeds the number of enzyme molecules. This situation is opposite that of the typical situation with soluble substrates, where access to the enzyme’s active site limits reaction. If we consider initial reaction rates and if the reaction is first order with respect to the concentration of enzyme bound to substrate (i.e., [ES]), then we can derive a rate expression:
where
and
The previous equation assumes slow binding of enzyme (i.e., [E] ≈ [E0]), S0 is the number of substrate bonds available initially for breakage, and kdes and kads refer to rates of enzyme desorption and adsorption onto the insoluble matrix, respectively.
3.2.6. Multiphase Enzymatic Reactions
Enzymes function in aqueous media, since most of the cells contain nearly 80% water yielding high water activity in the cytoplasm. When the substrate is effectively not soluble in aqueous media, but primarily soluble in an organic phase, then substrate containing organic phase and enzyme containing aqueous phase would have to come in contact for effective enzymatic catalysis (see Figure 3.16). Organic phase is assumed to be insoluble in water; and the solubility of the substrate between the organic and the aqueous phase differ greatly.
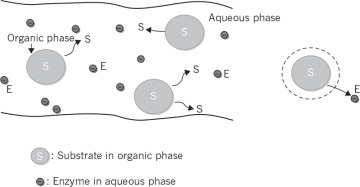
Figure 3.16. A schematic of the two-phase enzymatic reactions.
The substrate dissolved in the organic phase diffuses to the aqueous phase, and equilibrium is established between the two phases in the absence of reaction. The ratio of the solubilities of the substrate in organic and aqueous phase is known as the partition coefficient (p).
In this equation, So,e and Sw,e are the substrate concentrations in the organic and aqueous phases at equilibrium, respectively.
The rate of enzymatic reaction in the aqueous phase is limited typically by the rate of substrate transfer from the organic phase because the solubility of the substrate in aqueous phase is very low.
The rate of substrate transfer (RST) from the organic to the aqueous phase is as follows:
Here KL is the mass-transfer coefficient for the substrate transfer from organic to the aqueous phase; a is the interfacial area of the organic and aqueous phases per reaction volume (a = Ai/Vw); and So and Sw are the substrate concentrations in the organic and aqueous phases, respectively. No substrate transfer takes place when Sw = Sw,e.
The rate of enzymatic reaction in the aqueous phase is as follows:
At steady state, the substrate transfer and conversion rates are equal:
When the rate is severely mass-transfer limited, then Sw is negligible. In this case the rate of enzymatic reaction can be approximated as equal to the substrate transfer rate as follows:
In case of considerable substrate concentration in the aqueous phase, Sw is calculated from equation 3.56 in terms of the other parameters, and equation 3.54 or equation 3.55 can be used for calculation of the enzymatic reaction rate.
The substrate concentration in the aqueous phase can also be determined graphically. When the rate of substrate transfer and the enzymatic reaction rates were plotted with respect to Sw, the intersection point would yield the Sw on the x-axis and the rate of substrate transfer on the y-axis.


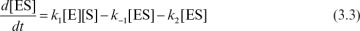




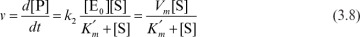



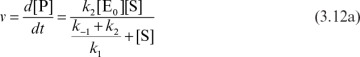





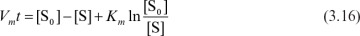
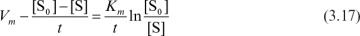
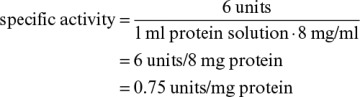

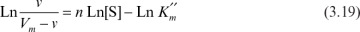
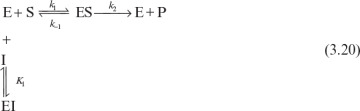
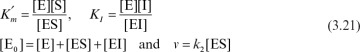


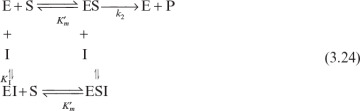
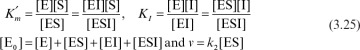


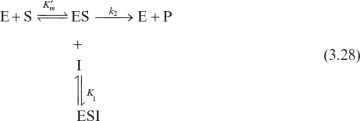
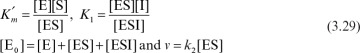


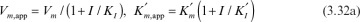
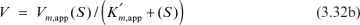

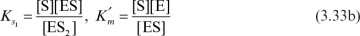






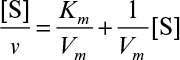
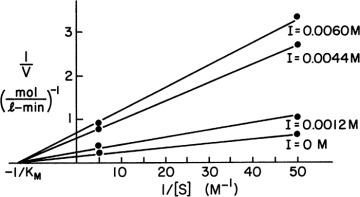
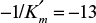 and
and 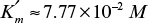 . For [S] = 0.2 M and I = 0 from the intercept of 1/V versus 1/S, 1/vm = 0.2 and Vm ≅ 5 mol/l-min. For I = 0.0012 M and [S] = 0.2 M, v = 3 mol/l-min. Substituting these values in
. For [S] = 0.2 M and I = 0 from the intercept of 1/V versus 1/S, 1/vm = 0.2 and Vm ≅ 5 mol/l-min. For I = 0.0012 M and [S] = 0.2 M, v = 3 mol/l-min. Substituting these values in