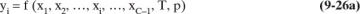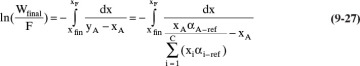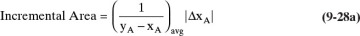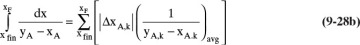- 9.0 Summary-Objectives
- 9.1 Introduction to Batch Distillation
- 9.2 Batch Distillation: Rayleigh Equation
- 9.3 Simple Binary Batch Distillation
- 9.4 Constant-Mole Batch Distillation
- 9.5 Batch Steam Distillation
- 9.6 Multistage Binary Batch Distillation
- 9.7 Multicomponent Simple Batch Distillation
- 9.8 Operating Time
- References
- Homework
- Chapter 9 Appendix A. Spreadsheet for Simple Multicomponent Batch Distillation, Constant Relative Volatility
This chapter is from the book
This chapter is from the book
This chapter is from the book
9.7 Multicomponent Simple Batch Distillation
In the derivation of the Rayleigh equation in section 9.1, we noted that the equations are valid for multicomponent mixtures. However, since the general equilibrium expression
)
depends on the concentration of all components, a numerical solution is required. We previously considered multicomponent simple batch distillation in section 8.5.2 when we discussed residue curves. Although the notations and the procedures are different, the developments in Sections 8.5.2 and 9.2.1 are equivalent (see Problem 9.C4). Thus, the residue curve gives us the path of the xi during the batch distillation, and from the required equilibrium calculation, it has also calculated the yi values that correspond to the xi, although the vapor values may not be reported. The profiles of xi and yi values are sufficient information to numerically integrate the Rayleigh equation.
The procedure is easiest to illustrate if the relative volatility is constant. For batch distillation the equilibrium expression, Eq. (5-28) given in Problem 5.C1, is
)
The Rayleigh equation for the light component A becomes
)
To numerically integrate the integral in Eq. (9-27), we start with the spreadsheet calculation of a residue curve (see Section 8.5.2 and Figure 8-B1). For each increment in k, the incremental area is
)
Then the calculated value of the integral is
)
where ΔxA,k = xA,k – xA,k–1, and (1/[yA – xA])avg = 0.5[(1/[yA – xA])k-1 + (1/[yA – xA])k].
For example, if we calculate the area for k = 10 for the spreadsheet in Figure 8-B1, we have
|ΔxA,k| = |0.989960081 – 0.990021592| = 0.000061511, and
1/(yA – xA)avg = 0.5[1/(0.99617266 – 0.990021592) + 1/(0.996149968 – 0.989960081)] = 162.06.
Incremental area = (0.000061511)(162.06) = 0.009969.
If the values of h and kfinal from a residue curve calculation using the Euler method (Section 8.5.2) starting with the initial conditions of the batch distillation are available, then an estimate of the area of the integral in Eq. (9-27) is
)
where kfinal is the step for which xA = xA,final. This equation is useful for checking the result of a numerical integration. The rationale behind Eq. (9-28c) is explored in Problem 9.C5.
EXAMPLE 9-3. Multicomponent simple batch distillation
A simple batch distillation of the ideal system benzene (B), toluene (T), and cumene (C) is run. Charge is 1.0 kmole, and the feed is 70.0 mol% benzene, 20.0 mol% toluene, and 10.0 mol% cumene. Determine Wfinal, Dtotal, xT,fin, xC,fin, xD,B,avg, xD,T,avg, and xD,C,avg if xB,fin = 0.4. Pressure is 1.0 atm, and the relative volatilities are αBT = 2.4, αTT = 1.0, and αCT = 0.21.
Solution
Define. The apparatus is shown in Figure 9-1. F = 1.0 kmol, xW,B,initial = 0.70, xW,T,initial = 0.20, xW,C,initial = 0.1, and xB,fin = 0.40. Find Wfinal, Dtotal, xT,fin, xC,fin, xdist,B,avg, xdist,T,avg, and xdist,C,avg.
Explore. We need to find the area of the integral in Eq. (9-27) so that we can calculate Wfinal. Once the total area has been found, Wfinal is given by Eq. (9-11b). The values of xT,fin and xC,fin can be determined from the residue curve. We can then find Dtotal from the overall mass balance, and the xdist,i,avg values are determined from component mass balances.
Plan. To find the integral of the area in Eq. (9-27) we can use a spreadsheet to generate a residue curve starting with the initial conditions. The values of xT,fin and xC,fin are on the residue curve at the value of xB,fin. The more accurate method to calculate the area is Eq. (9-28b). Thus, we will calculate the y values from Eq. (9-28b) for every step k in the calculation of the residue curve. Then 1/(y – x)avg can be calculated for each step k, and the area of each step can be determined.
Do It. The spreadsheet and VBA program for the calculations is shown in this chapter’s appendix with h = 0.001. The values in the spreadsheet at xB,fin = 0.4 are found by inspecting the output manually and are shown in Table 9.1.
The cumulative area at xB,fin = 0.40 is approximately 1.1919.
From these results, xT,fin = 0.3175, and xC,fin = 0.2825.
Wfinal = F exp(–Area) = 1.0 exp(–1.1919) = 0.3036 kmol
Dtotal = F – Wfinal = 1 – 0.3036 = 0.6964 kmol
xB,dist,avg = [FxB,init – WfinalxB,fin]/Dtotal = [0.7 – (0.3036)(0.4)]/0.6964 = 0.8308
xT,dist,avg = [FxT,init – WfinalxT,fin]/Dtotal = [0.2 – (0.3036)(0.3175)]/0.6964 = 0.1488
xC,dist,avg = [FxC,init – WfinalxC,fin]/Dtotal = [0.1 – (0.3036)(0.2825)]/0.6964 = 0.0204
TABLE 9-1. Results from spreadsheet to determine xB,fin = 0.4 and area
k
xB
xT
xC
yB
yT
yC
1/(yB-xB)
Cum. Area
1193
0.400051
0.3175
0.2824
0.71815
0.2375
0.0444
3.144
1.1917
1194
0.39973
0.3176
0.2827
0.71792
0.2377
0.0444
3.143
1.1927
Check. ∑ xi,dist,avg = 1.0000 which is OK.
In addition, the approximate solution for the area, Eq. (9-28c), gives
Area = (k – 1)h = (1193 – 1)(0.001) = 1.192
which agrees with the area calculation from the spreadsheet.
Generalize. This method can be applied to any number of components if the relative volatilities are constant.
If the relative volatilities are not constant, we have two choices. First, we can divide the range of the batch operation into a series of intervals and use an average value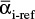 
for each interval. A reasonable definition of 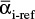is the geometric average for each interval:
)
){kind=link}
The recursion Eq. (8-30) uses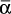 
values that correspond to the interval in which they appear.
The second procedure, which is more accurate, is to do a bubble-point calculation at every time step. The use of bubble-point calculations is explored in section 5.3 in the context of a steady-state, multistage analysis. For batch distillation the bubble-point calculation would be done at each step k. In essence, the resulting spreadsheet is a combination of the spreadsheets in Appendices 5A and 9A.
Fractions (Section 9.2.2) are often collected in multicomponent batch distillation. With only a single-stage, simple batch distillation does not give pure compounds unless the relative volatilities are very large. The calculation method is quite similar to the method shown in Example 9.3. For example, if a second fraction was collected for Example 9.3 when xW,B,2 = 0.3, we would look at the results of the spreadsheet in Appendix A to find the mole fractions and the cumulative area at this concentration. The values bracketing xW,B,2 = 0.3 are shown in Table 9.2.
TABLE 9-2. Calculations continuing Example 9.3 for fraction at xW,B,2 = 0.3
k |
xB |
xT |
xC |
yB |
yT |
yC |
1/(yB-xB) |
Cum. Area |
1497 |
0.30018 |
0.3364 |
0.3635 |
0.63579 |
0.2969 |
0.0674 |
2.9796 |
1.495699 |
1498 |
0.29984 |
0.3364 |
0.3637 |
0.63547 |
0.2971 |
0.0675 |
2.9795 |
1.496699 |
The cumulative area at xW,B,2 = 0.3 is approximately 1.4962. If we subtract this value from the cumulative area = 1.1919 at xW,B = 0.4, we determine the area for the fraction from xW,B = 0.4 to xW,B = 0.3 is 0.3043. The initial charge for this fraction was Wfinal = 0.3036 calculated in Example 9.3. Then W(at xW,B = 0.3) = (0.3036)exp(–0.3043) = 0.2239 kmole. (See Problem 9.D27a for an equivalent calculation and Problem 9.D27b for the completion of the problem.)
Obviously, multistage batch columns are also used for multicomponent separations. One fairly simple approach is to assume that the changes in the column are quite slow and use a steady-state analysis similar to that employed in Section 9.6 for binary separations. Examples are the Fenske-Underwood-Gilliland shortcut method or stage-by-stage calculation with bubble-point calculation on each stage. Since these analyses ignore holdup on the stages and dynamics of the stages, they are considered simple models. More complicated models include stage holdup and dynamics and may include a mass transfer analysis. Readers interested in these more advanced topics should consult Sorensen (2014) for references and Diwekar (2012) and Mujtaba (2004) for calculation details.