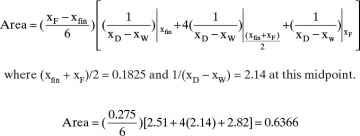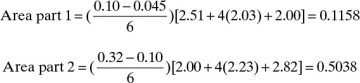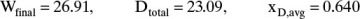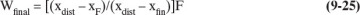- 9.0 Summary-Objectives
- 9.1 Introduction to Batch Distillation
- 9.2 Batch Distillation: Rayleigh Equation
- 9.3 Simple Binary Batch Distillation
- 9.4 Constant-Mole Batch Distillation
- 9.5 Batch Steam Distillation
- 9.6 Multistage Binary Batch Distillation
- 9.7 Multicomponent Simple Batch Distillation
- 9.8 Operating Time
- References
- Homework
- Chapter 9 Appendix A. Spreadsheet for Simple Multicomponent Batch Distillation, Constant Relative Volatility
9.6 Multistage Binary Batch Distillation
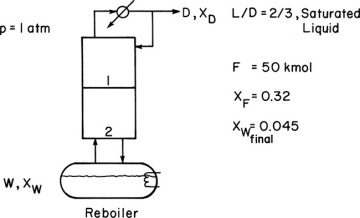
The separation achieved in a single equilibrium stage is often not large enough to obtain both the desired distillate concentration and a low enough bottoms concentration. In this case a distillation column is placed above the reboiler, as shown in Figure 9-2. The calculation procedure is detailed here for a staged column, but packed columns can easily be designed using the procedures explained in Chapters 10 and 16.
For multistage systems xD and xW are no longer in equilibrium. Thus, the Rayleigh equation, Eq. (9-7), cannot be integrated until a relationship between xD and xW is found. This relationship can be obtained from stage-by-stage calculations. We assume that there is negligible holdup on each plate, in the condenser, and in the accumulator. Then at any specific time we can write mass and energy balances around stage j and the top of the column, as shown in Figure 9-2A. These balances simplify to
Input = Output
since accumulation was assumed to be negligible everywhere except the reboiler. Thus, at any given time t
In these equations V, L, and D are molal flow rates. These balances are essentially the same equations we obtained for the rectifying section of a continuous column except that Eqs. (9-23) are time dependent. If we can assume constant molal overflow (CMO), the vapor and liquid flow rates will be the same on every stage, and the energy balance is not needed. Combining Eqs. (9-23a) and (9-23b) and solving for yj+1, we obtain the operating equation for CMO:
At any specific time Eq. (9-24) represents a straight line on a y-x diagram. The slope will be L/V, and the intercept with the y = x line will be xD. Since either xD or L/V will have to vary during the batch distillation, the operating line will change continuously.
9.6.1 Constant Reflux Ratio
The most common operating method is to use a constant reflux ratio and allow xD to vary. This procedure corresponds to a simple batch operation in which xD also varies. The relationship between xD and xW can now be found from a stage-by-stage calculation using a McCabe-Thiele analysis. Operating Eq. (9-24) is plotted on a McCabe-Thiele diagram for a series of xD values. Then we step off the specified number of equilibrium contacts on each operating line starting at xD to find the xW value corresponding to that xD. This procedure is shown in Figure 9-6 and Example 9-2.
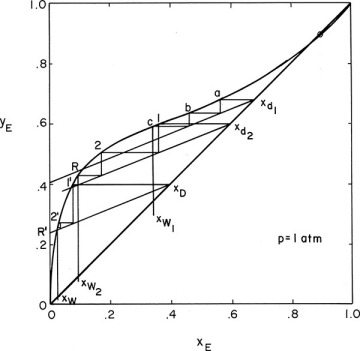
FIGURE 9-6 McCabe-Thiele diagram for multistage batch distillation with constant L/D, Example 9-2
The McCabe-Thiele analysis gives xW values for a series of xD values. We can now calculate 1/(xD – xW). The integral in Eq. (9-7) can be determined by either numerical integration, such as Simpson’s rule given in Eqs. (9-12a) to (9-12c), or by graphical integration. Once xW values have been found for several xD values, the same procedure used for simple batch distillation can be used. Thus, Wfinal is found from Eq. (9-7), xDavg from Eq. (9-8b), and Dtotal from Eq. (9-8a). If xDavg is specified, a trial-and-error procedure will again be required.
EXAMPLE 9-2. Multistage batch distillation
We wish to batch distil 50.0 kmol of a 32.0 mol% ethanol and 68.0 mol% water feed. The system has a still pot plus two equilibrium stages and a total condenser. Reflux is returned as a saturated liquid, and we use L/D = 2/3. We desire a final still-pot composition of 4.5 mol% ethanol. Find the average distillate composition, the final charge in the still pot, and the amount of distillate collected. Pressure is 1 atm.
Solution
Define. The system is shown in the following figure.
Find Wfinal, Dtotal, and xD,avg.
and C. Explore and Plan. Since we can assume CMO, a McCabe-Thiele diagram (Figure 2-2) can be used. This diagram relates xD to xW at any time. Since xF and xfin are known, the Rayleigh Eq. (9-7) can be used to determine Wfinal. Then Dtotal and xD,avg can be determined from Eqs. (9-8a) and (9-8b), respectively. A guess-and-check procedure is not needed for this problem.
Do it. The McCabe-Thiele diagram for several arbitrary values of xD is shown in Figure 9-6. The top operating line is
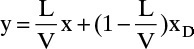
where
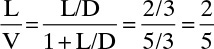
The corresponding xW and xD values are used to calculate xD – xW and then 1/(xD – xW) for each xW value. These values are plotted in Figure 9-7 (some values not shown in Figure 9-6 are shown in Figure 9-7). The area under the curve (going down to an ordinate value of zero) from xF = 0.32 to xfin = 0.045 is 0.608 by graphical integration.
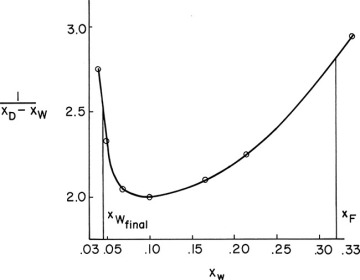
FIGURE 9-7 Graphical integration, Example 9-2
Then from Eq. (9-7),
Wfinal = Fe–Area = (50)exp(–0.608) = 27.21
From Eq. (9-8a),
Dtotal = F – Wfinal = 22.79
and from Eq. (9-8b),
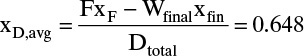
The area can also be determined by Simpson’s rule. However, because of the shape of the curve in Figure 9-7, it will be less accurate than in Example 9-1 unless the area is split into two or more parts. Simpson’s rule gives
This can be checked by breaking the area into two parts and using Simpson’s rule for each part. Do one part from xfin = 0.045 to xW = 0.10 and the other part from 0.1 to xF = 0.32. Each of the two parts should fit relatively well with a cubic. Then
Total area = 0.6196
Note that Figure 9-7 is very useful for finding the values of 1/(xD – xW) at the intermediate points xW = 0.0725 (value = 2.03) and xW = 0.21 (value = 2.23). The total area calculated is closer to the answer obtained graphically (1.9% difference compared to 4.7% difference for the first estimate).
Then doing the same calculations as previously [Eqs. (9-7), (9-8a), and (9-8b)] with Area = 0.6196,
Check. The mass balances for an entire cycle, Eqs. (9-1) and (9-2), should be and are satisfied. Since the graphical integration and Simpson’s rule (done as two parts) give similar results, this is another reassurance.
Generalize. Note that we did not need to find the exact value of xD that corresponds to xF or xfin. We just made sure that our calculated values went beyond these values and then used Figure 9-7 to interpolate to find values for Simpson’s rule. This is true for both integration methods. Our axes in Figure 9-7 were selected to give maximum accuracy; thus, we did not graph parts of the diagram that we did not use. The same general idea applies if fitting data—fit the data only in the region needed. For more accuracy, Figure 9-6 should be expanded. If Simpson’s rule is to be used for very sharply changing curves or curves with maxima or minima, accuracy is better if the curve is split into two or more parts. Comparison of the results obtained with graphical integration to those obtained with the two-part integration with Simpson’s rule shows a difference in xD,avg of 0.008. This is within the accuracy of the equilibrium data.
Once xfin, D, and Wfinal are determined, we can calculate the values of Qc, QR, and operating time (see Section 9.8).
9.6.2 Variable Reflux Ratio
Batch distillation columns can also be operated with a variable reflux ratio to keep xD constant. Operating Eq. (9-24) is still valid, the intersection with the y = x line will be constant at xD, but the slope varies. The McCabe-Thiele diagram for this case relating xW to xD is shown in Figure 9-8. Since xD is kept constant, the calculation procedure is simplified.
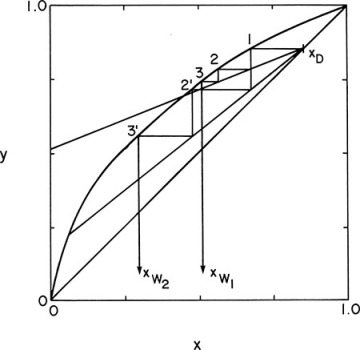
FIGURE 9-8 McCabe-Thiele diagram for multistage batch distillation with constant xD and variable reflux ratio
With xD and the number of stages specified, trial and error is required to find the initial value of L/V that gives the feed concentration xF with the specified number of stages. The operating line slope L/V is then increased until the specified number of equilibrium contacts gives xW = xfin. This gives (L/V)final. Wfinal is found from mass balance Eqs. (9-1) and (9-2).
The required maximum values of Qc and QR and the operating time can be determined next (see Section 9.8). Note that the Rayleigh equation is not required when xD is constant. However, if used, the Rayleigh equation gives exactly the same answer as Eq. (9-25) (see Problem 9.C1).