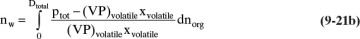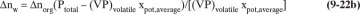- 9.0 Summary-Objectives
- 9.1 Introduction to Batch Distillation
- 9.2 Batch Distillation: Rayleigh Equation
- 9.3 Simple Binary Batch Distillation
- 9.4 Constant-Mole Batch Distillation
- 9.5 Batch Steam Distillation
- 9.6 Multistage Binary Batch Distillation
- 9.7 Multicomponent Simple Batch Distillation
- 9.8 Operating Time
- References
- Homework
- Chapter 9 Appendix A. Spreadsheet for Simple Multicomponent Batch Distillation, Constant Relative Volatility
9.5 Batch Steam Distillation
In batch steam distillation, steam is sparged directly into the still pot, as shown in Figure 9-5. This is normally done for systems that are immiscible with water. The reasons for adding steam directly to the still pot are that it keeps the temperature below the boiling point of water, it eliminates the need for heat transfer surface area, and it helps keep slurries and sludges well mixed so that they can be pumped. The major use is in treating wastes that contain valuable volatile organics. These waste streams are often slurries or sludges that foul heat exchanger surfaces and are difficult to process in an ordinary batch still. Glycerin, lube oils, fatty acids, and halogenated hydrocarbons are often steam distilled (Woodland, 1978). Section 8-3 is a prerequisite for this section.
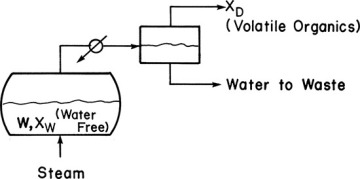
FIGURE 9-5 Batch steam distillation
Batch steam distillation is usually operated with liquid water present in the still. Then both the liquid water and the liquid organic phases exert their own partial pressure. Equilibrium is given by Eqs. (8-14) to (8-18) when there is one volatile organic and some nonvolatile organics present. As long as there is minimal entrainment, there is no advantage in the separation to having more than one stage, but steam use can be reduced. For low-molecular-weight organics, vaporization efficiencies, defined as the actual partial pressure divided by the partial pressure at equilibrium, p*,
are often in the range from 0.9 to 0.95 (Carey, 1950). This efficiency is close enough to equilibrium that equilibrium calculations are usually adequate.
The mass balances for Figure 9-5 are typically written on a water-free basis. These balances are identical in form to Eqs. (9-1) and (9-2) and can be solved for Wfinal if xfin is known.
On a water-free basis F, Wfinal, and D are kmol organics in the feed, still pot, and distillate, respectively. The mole fractions x are (moles volatile organic)/(total moles organic). With a single volatile organic, xD,avg = 1.0 if entrainment is negligible. Then
and the amount of the organic distillate product is given by Eq. (9-8a), D = F – Wfinal. The Rayleigh equation can also be used and will give the same results.
At any moment the instantaneous moles of water dnw carried over in the vapor can be found from Eq. (8-18). This becomes
The total moles of water carried over in the vapor can be obtained by integrating this equation:
During the batch steam distillation, the mole fraction of the volatile organics in the still varies, and thus, the still temperature determined by Eq. (8-15) varies. Equation (9-21b) can be integrated numerically in steps. The total moles of water required is nw plus the moles of water condensed to heat the feed and still pot and to vaporize the volatile organics.
To integrate Eq. (9-21b) we must relate the moles of the volatile organic in the distillate, norg, to its mole fraction in the still pot, xpot = xvolatile. From a mass balance on the volatile organic very similar to that used to derive Eq. (9-20b), we obtain
This equation is valid at any time. As the mole fraction of the volatile organic in the still pot, xpot, decreases, the moles of volatile organic collected in the distillate, norg, increase.
For step-by-step numerical integration, Eq. (9-21b) can be written as
The total change in the mole fraction of volatile organic as xpot goes from xF to xw,final can be broken up into a number of intervals, Δxpot. In each interval norg, xpot,average, and Δnw are calculated. The amount of water carried over into the distillate with the volatile organic is given by Eq. (9-22c). The calculation becomes more accurate as more intervals are used in the range from xF to xw,final.
A short example for the simplified case in which the temperature in the still pot does not vary much and (VP)volatile is essentially constant will help to clarify the procedure. Suppose F = 1.0 kmol, xF = 0.35, Ptotal = 760 mm Hg, (VP)volatile = 50 mm Hg, and we want to calculate Δnw for a change in xpot from 0.25 to 0.20. Then from Eq. (9-22a) at xpot = 0.25,
norg = F(xF – xpot)/(1 – xpot) = 1.0(0.35 – 0.25)/(1 – 0.25) = 0.13333
At xpot = 0.20, norg = 0.18750. In the interval from xpot = 0.25 to xpot = 0.20, xpot,average = 0.225, and Δnorg = 0.18750 – 0.13333 = 0.05417. Then from Eq. (9-22b),
Δnw = 0.05417[760 – (50)(0.225)]/[(50)(0.225)] = 3.605 kmol water.
If the still pot temperature varies significantly, the temperature at each value of xpot,average needs to be determined from Eq. (8-15) so that the value of (VP)volatile can be calculated. This is easiest to do with a spreadsheet.
During most of the batch operation, the mole fraction of the volatile organic is considerably higher than it is at the end of the batch. In continuous steam distillation the mole fraction of the volatile organic is always at its lowest value. Thus, batch steam distillation requires less steam for a given separation than continuous steam distillation.