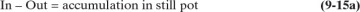- 9.0 Summary-Objectives
- 9.1 Introduction to Batch Distillation
- 9.2 Batch Distillation: Rayleigh Equation
- 9.3 Simple Binary Batch Distillation
- 9.4 Constant-Mole Batch Distillation
- 9.5 Batch Steam Distillation
- 9.6 Multistage Binary Batch Distillation
- 9.7 Multicomponent Simple Batch Distillation
- 9.8 Operating Time
- References
- Homework
- Chapter 9 Appendix A. Spreadsheet for Simple Multicomponent Batch Distillation, Constant Relative Volatility
This chapter is from the book
This chapter is from the book
This chapter is from the book
9.4 Constant-Mole Batch Distillation
One relatively common application of batch distillation (or evaporation) is to switch solvents in a production process. For example, solvents may need to be exchanged prior to a crystallization or reaction step. Solvent switching can be done by charging the still pot with feed, concentrating the solution (if necessary) by boiling off most of the original solvent (some solvent needs to remain to maintain agitation, keep the solute in solution, and keep the heat transfer area covered), adding the new solvent, and doing a second batch distillation to remove the remainder of the original solvent. If desired the solution can be diluted by adding more of the desired solvent. Although this process mimics the procedure used by bench chemists, a considerable amount of the second solvent is evaporated in the second batch distillation. An alternative is to do the second batch distillation by constant-mole batch distillation in which the pure second solvent is added continuously during the second batch distillation at a rate that keeps the moles in the still-pot constant (Gentilcore, 2002). This section focuses on the constant-mole batch distillation step.
For a constant-mole batch distillation the general mole balance is
)
For the total mole balance this is In – Out = 0, since the moles in the still pot are constant. Thus, if dS moles of the second solvent are added, the overall mole balance for a constant-mole batch distillation is
)
where dV is the moles of vapor withdrawn.
If we do a component mole balance on the original solvent (solute is assumed to be nonvolatile and is ignored), we obtain the following for a constant-mole system,
)
where y and xw are the mole fraction of the first solvent in the vapor and liquid, respectively. Substituting in Eq. (9-15b), this becomes
)
Note that since the amount of liquid W is constant, there is no term equivalent to the last term in Eq. (9-4). Integration of Eq. (9-16b) and minor rearrangement gives us
)
Since vapor and liquid are assumed to be in equilibrium, y is related to xw by the equilibrium relationship. Equation (9-17) can be integrated graphically or numerically in a procedure that is quite similar to that used for simple batch distillation. Problem 9.D17 leads you through these calculations for constant-mole batch distillation.
If constant relative volatility between the two solvents can be assumed, Eq. (2-22) can be substituted into Eq. (9-17), and the equation can be integrated analytically (Gentilcore, 2002):
)
Gentilcore presents a constant relative volatility sample calculation that illustrates the advantage of constant-mole batch distillation when it is used to exchange solvents. The method for obtaining accurate results for low values of xfin outlined in the last paragraph of Example 9-1 can be used for constant-mole batch distillation by replacing Eq. (9-13) with Eq. (9-18).
The amount of new solvent required can be reduced by putting a column above the still pot. Equation (9-17) remains valid except y is now the vapor leaving the top of the column (the same mole fraction as xdist if there is a total condenser), and y is not in equilibrium with the still-pot liquid. The procedures outlined in Section 9.6 for multistage systems can be used to determine the separation.