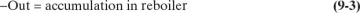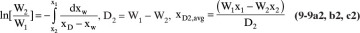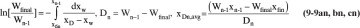- 9.0 Summary-Objectives
- 9.1 Introduction to Batch Distillation
- 9.2 Batch Distillation: Rayleigh Equation
- 9.3 Simple Binary Batch Distillation
- 9.4 Constant-Mole Batch Distillation
- 9.5 Batch Steam Distillation
- 9.6 Multistage Binary Batch Distillation
- 9.7 Multicomponent Simple Batch Distillation
- 9.8 Operating Time
- References
- Homework
- Chapter 9 Appendix A. Spreadsheet for Simple Multicomponent Batch Distillation, Constant Relative Volatility
9.2 Batch Distillation: Rayleigh Equation
The mass balances for batch distillation are somewhat different from those for continuous distillation. In batch distillation we are more interested in the total amounts of bottoms and distillate collected than in the rates. For a batch distillation, the overall mass balance around the entire system for the entire operation time is
The mass balance on any component, typically the light component is,
For a multicomponent feed Eq. (9-2) can be written for C-1 of the C components. The feed into the column is F kmoles of mole fraction xF of the more volatile component (MVC). At the end of the batch there are Wfinal kmoles of mole fraction xfin in the still pot. The symbol W is used since the material left in the reboiler is often a waste. Dtotal is the total kmoles of distillate of average concentration xD,avg. Equations (9-1) and (9-2) are applicable to simple batch and normal multistage batch distillation. Some minor changes in variable definitions are required for inverted batch distillation. If fractions are collected, Dtotal is split into a series of distillate fractions (see Section 9.2.2).
9.2.1 Mixed Distillate Product
A common way to operate simple batch distillation is to mix all the distillate and produce a single distillate product. Usually F, xF, and the desired value of either xfin or xD,avg for the light component are specified. An additional equation is required to solve for the three unknowns, Dtotal, Wfinal, and xfin (or xD,avg). This additional equation, called the Rayleigh equation (Rayleigh, 1902), is derived from a differential mass balance on the light component. Assume that the holdup in the column and in the accumulator is negligible. Then if a differential amount of material, –dW, of concentration xD is removed from the system, the differential component mass balance is
or
Expanding Eq. (9-4),
Then rearranging
and integrating
which is
The minus sign comes from switching the limits of integration. Equation (9-7) is a form of the Rayleigh equation that is valid for both simple and multistage and for binary and multicomponent batch distillation. Of course, to use this equation we must relate xD to xW and do the appropriate integration. This is covered in sections 9.3 and 9.6. Time does not appear explicitly in the derivation of Eq. (9-7), but it is implicitly present since W, xW, and usually xD are all time dependent (see Section 9.8).
Once Wfinal has been determined D can be determined from the overall mass balance
and the average distillate concentration can be found from a mass balance on the MVC.
9.2.2 Distillate Product Fractions
Another common operating method for batch distillation, particularly for multicomponent mixtures, is to collect different distillate fractions, 1, 2, 3, ..., with distillate amounts, D1, D2, D3, ..., collected when the still pot has W1, W2, W3, ... moles remaining in it with mole fractions x1, x2, x3, .... For the first period the Rayleigh equation is
The amount of distillate collected during this period is
And the mole fraction of the component in this distillate fraction is
The initial amount in the still pot for the second period (essentially the feed for this period) is W1 with mole fraction x1. Then the Rayleigh equation, distillate amount, and distillate mole fraction become
The fractions continue until the last fraction n:
Equations (9-9) are valid for both simple binary batch and multistage binary batch distillation. If these equations are written for C-1 components, they are also valid for multicom-ponent systems.
If fractions with sharp cuts are desired, you can either add a large number of stages to the column or take a waste, or offcut, between the desired product fractions, as shown in Figure 9-3 (Sorensen, 2014). The offcuts are usually reprocessed in the next batch. Equations (9-9) are still valid, but some of the fractions are products, and some are offcuts. The taking of offcuts is explored in Problem 9.D26 for simple binary batch distillation.
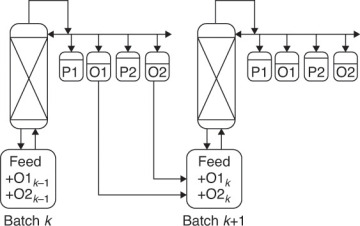
FIGURE 9-3 Batch distillation with distillate product cuts (P1 and P2) and offcuts (O1 and O2). From Sorensen, E., “Design and Operation of Bach Distillation,” in Gorak, A. and E. Sorensen (Eds.), Distillation. Fundamentals and Principles, Chapter 5, Elsevier, London, UK, 2014. Reprinted with permission of Elsevier. Copyright 2014.