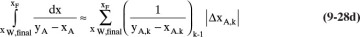Batch Distillation

This chapter is from the book

Separation Process Engineering: Includes Mass Transfer Analysis, 4th Edition

Learn More Buy

This chapter is from the book

This chapter is from the book 

Separation Process Engineering: Includes Mass Transfer Analysis, 4th Edition

Learn More Buy

Homework

• A. Discussion Problems

  A1. Why is the still pot in Figure 9-2B much larger than the column?

  A2. In the derivation of the Rayleigh equation:

  1. In Eq. (9-4), why do we have –x_D dW instead of –x_D dD?

  2. In Eq. (9-4), why is the left-hand side –x_D dW instead of –d(x_DW)?

  A3. Explain how the graphical integration shown in Figures 9-3 and 9-5 could be done numerically on a computer.

  A4. Suppose you have two feeds containing methanol and water that you want to batch distil. One feed is 60.0 mol% methanol, and the other is 32.0 mol% methanol. How do you do the batch distillation to obtain the largest amount of distillate of a given mole fraction? N is constant.

  1. Mix the two feeds together and batch distil.

  2. Start the batch with the feed with higher methanol mole fraction and then add second feed (32.0 mol% methanol) when the still-pot concentration equals that feed concentration.

  3. Do two separate batches—one for the more concentrated feed (60.0 mol%) and the other for the less concentrated feed (32.0 mol%).

  4. All of the above.

  5. a and b.

  6. a and c.

  7. b and c.

  8. None of the above.

      Explain your answer.

  A5. Which system(s) require less energy for batch distillation than continuous distillation with the same amount of separation?

  1. Simple batch compared to one-stage continuous.

  2. Multistage batch compared to multistage continuous.

  3. Batch steam distillation compared to continuous steam distillation.

  4. All of the above.

  5. a and b.

  6. a and c.

  7. b and c.

  8. None of the above.

      Explain your answer.

  A6. Batch-by-Night, Inc., has developed a new simple batch with reflux system (Figure 9-1 with some of stream D refluxed to the still pot) that they claim outperforms the normal simple batch (Figure 9-1). Suppose you want to batch distil a mixture similar to methanol and water in which there is no azeotrope and two liquid phases are not formed. Both systems are loaded with the same charge F moles with the same mole fraction x_F, and distillation is done to the same value x_w,final. Will the value of x_d,avg from the simple batch with reflux be

  1. greater than

  2. the same as

  3. less than

  the x_d,avg value from the normal, simple batch distillation? Explain your answer.

  A7. When there are multiple stages in batch distillation, the calculation looks like the McCabe-Thiele diagram for several

  1. stripping columns.

  2. enriching columns.

  3. columns with a feed at the optimum location.

  A8. Develop a key relations chart for this chapter.

  A9. If we are doing a batch distillation of a heterogeneous azeotrope system, when would we employ a system similar to Figure 9-1, and when would we employ a system similar to Figure 9-10 (in Problem 9.D9)?

• B. Generation of Alternatives

  B1. List all the different ways a binary batch or inverted batch problem can be specified. Which of these will be trial and error?

  B2. What can be done if an existing batch system cannot produce the desired values of x_D and x_W even at total reflux? Generate ideas for both operating and equipment changes.

  B3. Develop ideas for how you would reprocess or utilize the offcuts from a batch distillation that collects fractions.

• C. Derivations

  C1. For a binary multistage batch distillation with constant x_dist, prove that the mass balances over the entire batch period and the Raleigh equation both give Eq. (9-25).

  C2. Assume that holdup in the column and in the total reboiler is negligible in an inverted batch distillation (Figure 9-9).

  1. * Derive the appropriate form of the Rayleigh equation.

  2. Derive the necessary operating equations for CMO. Sketch the McCabe-Thiele diagrams.

  

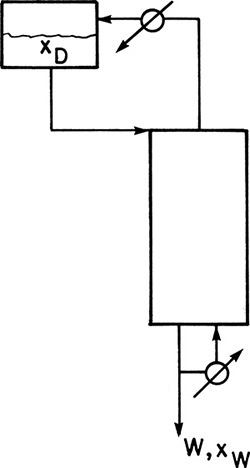
  FIGURE 9-9 Inverted batch distillation

  C3. If relative volatility can be assumed constant over the change in concentration for each fraction, Eq. (9-13) can be adapted to the collection of fractions from a simple binary batch distillation. Derive the equations for a simple batch with three distillate fractions collected.

  C4. Show that Eq. (9-5c) [immediately before Eq. (9-14)] is equivalent to Eq. (8-27c).

  C5. If we approximate the area in Eq. (9-28b) as

  

  Click to view larger image

  then the incremental area for k = 10 (see the section immediately before Example 9.3) = (0.000061511)(162.573393759) = 0.01000005 = h = 0.01. From this result, you can deduce the approximate Eq. (9-28c).

  1. Prove that this agreement of the numerical value of the estimated incremental area and the value of h is not an accident.

  2. Explain how Eq. (9-28c) can be deduced.

  3. Check the prediction of Eq. (9-28c) for Example 9.3.

  4. Problems

  *Answers to problems with an asterisk are at the back of the book.

  D1. A simple batch distillation separates 0.6 kmol of a binary feed that is 70.0 mol% methanol and 30.0 mol% water. The final still pot is 10.0 mol% methanol. Find W_final, distillate D_total, and x_D,avg. VLE data are in Table 2-7. p = 1.0 atm.

  D2.* A simple batch still (one equilibrium stage) separates 100 moles of a 75.0 mol% methanol and 25.0 mol% water feed. The final bottoms concentration is 55.0 mol% methanol. Find W_final, distillate D_total, and x_D,avg. VLE data are in Table 2-7. p = 1.0 atm.

  D3.* A distillation system with a still pot plus a column with one equilibrium stage is used to batch distil 1.0 kmol of a 57.0 mol% methanol and 43.0 mol% water feed. A total condenser is used. The final bottoms concentration is 15.0 mol% methanol. Pressure is 101.3 kPa. Reflux is a saturated liquid, and L₀/D = 1.85. Find W_final, D_total, and x_D,avg. VLE data are in Table 2-7.

  D4. A simple batch distillation (one equilibrium contact) is done of an 80.0 mol% acetone and 20.0 mol% ethanol feed. The final concentration in the still pot is 40.0 mol% acetone, and W_final = 2.0 kmole. VLE data are in Problem 4.D7. Find the feed amount F, the average mole fraction of the distillate, and the kmoles of distillate D_total collected.

  D5. 3.0 kmol of feed containing 52.0 mol% water and 48.0 mol% n-butanol is charged to the still pot of a simple batch distillation system (Figure 9-1). The final still pot concentration should be 28.0 mol% water. Equilibrium data are in Table 8-2.

  1. Find W_final (kmole), D_V,tot (total amount of distillate vapor collected, kmole), and y_D,avg (average mole fraction water in the vapor distillate).

  2. After the distillate vapor is condensed in the total condenser, the liquid is sent to a liquid-liquid settler. Find the total amount of each distillate liquid collected, D₁ (with x_D1,water = 0.573) and D₂ (with x_D2,water = 0.975), in kmoles.

  D6. A simple batch still separating a feed that is 60.0 mol% 1,2 dichloroethane and 40.0 mol% 1,1,2-trichloroethane. Pressure is 1 atm. The relative volatility is constant, α_di-tri = 2.4. The use of Eq. (9-13) is recommended.

  1. The charge (F) is 1.3 kmol. The final still pot concentration is 30.0 mol% 1,2 dichloroethane. Find the final moles in still pot and the average mole fraction of distillate product.

  2. Repeat part a if F = 3.5 kmol.

  3. If F = 2.0 kmol and the average distillate concentration is 75.0 mol% 1,2-dicholoroethane, find final kmoles in the still pot and the final mole fraction of 1,2 dichloroethane in the still pot.

  D7. A batch distillation system with a still pot and one equilibrium stage (two equilibrium contacts total) distills a feed that is 10.0 mol% water and 90.0 mol% n-butanol (see Table 8-2 for VLE data). p = 1.0 atm. The charge is 4.0 kmoles. The final still concentration is 2.0 mol% water. The system has a total condenser, and the reflux is a saturated liquid. L/D = 1/2. Find the final number of moles in the still pot and the average concentration of distillate.

  D8. 10.0 kmol of a feed with x_F = 0.4 (mole fraction methanol) and the remainder water is sent to a batch distillation system with a large still pot that is an equilibrium contact, a distillation column that acts as two equilibrium contacts (total three equilibrium contacts), and a total condenser. p = 1.0 atm. We operate with a constant x_D = 0.8 as we increase L/D. The batch operation is continued until L/D = 4.0. CMO is valid. VLE data are in Table 2-7. Find:

  1. x_w,final.

  2. W_final and D_total.

  3. Initial L/D.

  D9.* We wish to batch distil a mixture of 1-butanol and water. Since this system has a heterogeneous azeotrope (see Chapter 8), we will use the system shown in Figure 9-10. The bottom liquid layer from the liquid-liquid separator (97.5 mol% water) is removed as product, and the top liquid layer (57.3 mol% water) is returned to the still pot. Pressure is 1 atm. The feed is 20.0 kmol and 40.0 mol% water. Data are given in Problem 8.D2.

  1. If the final concentration in the still pot is x_W,final = 0.28, find D_total in kmoles.

     

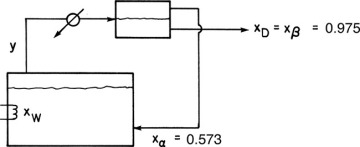
     FIGURE 9-10 Batch distillation system with reflux for heterogeneous azeotrope

  2. If the batch distillation is continued what is the lowest value of x_W,final that can be obtained while still producing a distillate x_D = 0.975?

  D10. 4.0 kmoles of a feed that is 0.60 mole fraction acetone and 0.40 mole fraction ethanol is batch distilled in a system with a still pot (an equilibrium contact), a column that acts as one equilibrium stage (total two equilibrium contacts), a total condenser, and reflux to the column. p = 1.0 atm, the reflux ratio is L/D = 1.0, CMO is valid, and x_W,final = 0.20. VLE data are in Problem 4.D7. Find W_final, x_dist,avg, and D_total.

  D11. A constant-mole batch distillation is used to change from a pure n-butanol solvent to a solvent that is 60.0 mol% n-butanol and 40.0 mol% water. If the initial charge is W = 2.0 kmol, how much water, S, must be added to achieve the desired solvent concentration? Do the integration with Simpson’s rule, dividing the entire integration from 0.6 to 1.0 first into one step and then into two steps. Compare the answers.

  D12. A nonvolatile pharmaceutical is dissolved in a solution that is 90.0 mol% acetone and 10.0 mol% ethanol. A constant volume batch distillation is used to switch the solvent to 20.0 mol% acetone and 80.0 mol% ethanol without diluting the concentration of solute. The charge to the still pot is W = 1.5 kmol. VLE data are in Problem 4.D7. What are the values of the amount (kmol) of pure solvent ethanol added, the kmol of acetone that are evaporated, the kmol of ethanol evaporated, and the average mole fraction of acetone in the distillate?

  D13. A simple batch distillation (Figure 9-1) is separating 8.00 kmol of a feed that is 40.0 mol% water and 60.0 mol% n-butanol. The batch distillation is continued until the still pot contains 0.080 mole fraction water. VLE data are in Table 8-2, Problem 8.D3.

  1. Find W_final, D_total, and x_D,avg.

  2. After settling, the final distillate product is two liquid phases. What are the mole fractions and the amounts (kmol) of each liquid phase?

  Note: Problem 9.D28 shows that Figure 9-10 gives a better separation.

  D14.* A simple steam distillation is being done in the apparatus shown in Figure 9-5. The organic feed is 90.0 mol% n-decane and 10.0% nonvolatile organics. The system is operated with liquid water in the still. Distillation is continued until the organic layer in the still is 10.0 mol% n-decane. F = 10 kmole. Pressure is 760 mm Hg.

  1. At the final time, what is the temperature in the still?

  2. What are values of W_final and D_total?

  3. Estimate the moles of water passed overhead per mole of n-decane at the end of the distillation.

  Data: Assume that water and n-decane are completely immiscible. Vapor pressure data for nC₁₀ are in Example 8-2. Vapor pressure data for water are listed in Problem 8.D10.

  D15. 12.0 kmole of a mixture 0.40 mole fraction water and 0.60 mole fraction n-butanol at 1.0 atm pressure is batch distilled in a system with an equilibrium still pot and a column with one equilibrium stage (total two equilibrium contacts). Vapor from the column is sent to a total condenser and then to a liquid-liquid settler. The aqueous phase from the settler (0.975 mole fraction water) is removed as the distillate product. The organic phase from the settler (0.573 mole fraction water) is refluxed to the distillation column. (The equipment is a modification of Figure 9-10 with a column between the still pot and the condenser.) D_total = 3.9 kmol. Equilibrium data are in Table 8-2 (in Problem 8.D3).

  1. Find W_final and x_W,final.

  2. Find the approximate value of the reflux ratio L/D at end of the batch distillation.

  D16.* 10.0 kmol of a 40.0 mol% methanol and 60.0 mol% water mixture is processed in a normal batch distillation system with a still pot that acts as an equilibrium stage and a column with two equilibrium stages (total of three equilibrium contacts). The column has a total condenser, and reflux is a saturated liquid. The column is operated with a varying reflux ratio so that x_D is held constant. We desire a final still-pot concentration of 8.0 mol% methanol, and distillate should be 84.0 mol% methanol. Pressure is 1 atm, and CMO is valid.

  1. What initial external reflux ratio, L₀/D, must be used?

  2. What final external reflux ratio must be used?

  3. How much distillate product is withdrawn, and what is the value of W_final?

  D17. A nonvolatile solute is dissolved in 1.0 kmol of methanol. We wish to have the solute in 1.0 kmol of solution that is 99.0 mol% water and 1.0 mol% methanol. Because the solution is already concentrated, a first batch distillation to concentrate the solution is not required. VLE data (ignore the effect of the solute) are in Table 2-7. Do a constant-mole batch distillation from x_M,initial = 1.0 (pure methanol) to x_M,final = 0.01. Find the moles of water added during the constant-mole batch distillation and the moles of water evaporated with the methanol in the distillate. Results can be compared with dilution followed by simple batch distillation in Problem 9.E4.

  Note: Since x_M,final = 0.01 is quite small, 1/y is quite large at this limit. To use Simpson’s rule divide the integral into at least two sections.

  D18. A differential condensation [see Eq. (9-14)] is done for a binary mixture of ethanol and water. The feed is 0.50 kmol of vapor that is 0.10 mole fraction ethanol. The differential condensation is continued until the vapor remaining is y_D,final = 0.50 mole fraction ethanol. Find the values of D_final and the condensate C_total and the average mole fraction of ethanol in the condensate, x_C,avg. Note that this operation can only be approximated in practice (Treybal, 1980). Compare the result to the solution to Problem 9.D1.

  D19. Batch steam distillation is being done to recover octanol from nonvolatile organics. Assume that water and octanol, and water and the nonvolatile organics are completely immiscible. The water layer is pure. The organic layer in the still pot contains 0.60 mole fraction octanol and 0.40 mole fraction nonvolatile organics. The still pot temperature is 90.0°C. The Antoine equations (T is in °C, and VP is the vapor pressure in mm Hg) are:

  Octanol: log₁₀ (VP) = 6.8379 – 1310.62/(T + 135.05)

  Water: log₁₀ (VP) = 8.68105 – 2164.42/(T + 273.16)

  What is the pressure of the still pot?

  D20. 10.0 kmole of a 40.0 mol% methanol and 60.0 mol% water mixture is batch distilled. The system consists of a column with two equilibrium stages, a still pot (an equilibrium contact), and a total condenser. The system is operated with a reflux ratio L/D = 0.515. The final concentration of methanol in the still pot is x_W,final = 0.075. CMO is valid. If you use Simpson’s rule, break the area into at least two parts. Find W_final, D_total, and x_dist,avg.

  D21. Repeat Problem 9.D20 but for a distillation column with 20 stages.

  Note: Think smart and this problem is significantly less work than Problem 9.D20.

  D22. 3.0 kmol of a 62.0 mol% methanol and 38.0 mol% water are batch distilled in a system with a still pot and a column with one equilibrium stage (two equilibrium contacts total). Distillate concentration is constant at 85.0 mol% methanol. The final still pot concentration is 45.0 mol% methanol. Reflux is a saturated liquid, and L/D varies. Assume CMO.

  1. Find D_total and W_final (kmoles).

  2. Find the final value of the external reflux ratio L/D.

  D23.* 1.2 kmol of a 10.0 mol% ethanol and 90.0 mol% water feed is processed in a simple batch distillation system that consists of a still pot, a total condenser, and a fraction collector. We collect three fractions with x_W1 = 7.0 mol% ethanol, x_W2 = 4.0 mol% ethanol, and x_W3 = x_W,final = 1.0 mol% ethanol. Find W₁, W₂, and W_final; D₁, D₂, and D₃ in kmole; and mole fractions of ethanol x_D1,avg, x_D2,avg, and x_D3,avg. p = 1.0 atm.

  D24. A constant-mole batch distillation is being done to replace methanol with water as solvent for a nonvolatile solute currently dissolved in methanol. The system has a still pot and a condenser and operates with no reflux. The initial state has W_initial = 10.0 kmol, and x_{w,MeOH,initial} = 1.00. The final state has W_final = 10.0 kmol, x_w,MeOH,final = 0.10, and x_{w,water,final} = 0.90 mole fraction. Pressure = 1.0 atm.

  1. Find S, the kmol of water added, and D_total = kmol of distillate.

  2. Find the average distillate mole fraction of methanol, x_{dist,MeOH,avg}.

  3. If the heating rate is constant at 100 kW, how many hours does the constant mole batch distillation require (assume water is added as a saturated liquid)?

  D25. 1.5 kmol of feed one that is 40.0 mol% methanol and 60.0 mol% water and 1.0 kmol of feed two that is 20.0 mol% methanol and 80.0 mol% water will be processed in a simple batch distillation. The following three approaches have been proposed:

  1. Mix the two feeds together, and do the batch distillation.

  2. Do a batch distillation of feed one until the still pot concentration is 20 mol% methanol (same as feed two), add feed two, and then complete the batch distillation.

  3. Do a batch distillation of feed one and a separate batch distillation of feed two. Add the two distillate products and the two still-pot products.

  If we want x_{W,final,total} = 0.10, do calculations for each method. Determine W_final, D_total, and x_D,average, and compare the three methods. Equilibrium data are in Table 2-7. Logically, parts b and c should give the same result. If they do not, there is probably a numerical error from the use of Simpson’s rule. Try dividing an area into two parts for more accuracy.

  D26. In Problem 9.D23 fractions were collected from ethanol mole fractions x_F = 0.10 to x_W1 = 0.07, from x_W1 to x_W2 = 0.04, and from x_W2 to x_W3 = x_W,final = 0.01. The solution is given under Answers to Selected Problems. Now collect a first product fraction (A) from x_F = 0.10 to x_WA = 0.085, a second product fraction (B) from x_WOC1 = 0.07 to x_WB = 0.05, and a third product fraction (C), which is identical to the current fraction, 3. To obtain these product fractions we need two offcuts: OC1 from x_WA = 0.085 to x_WOC1 = 0.07, and OC2 from x_WB = 0.05 to x_WOC2 = 0.04.

  1. Find W and D (in kmol) and the mole fractions of ethanol x_D,avg for each fraction.

  2. How would you reprocess the offcuts in the next batch?

  D27. The continuation of Example 9.3 in Table 9.2 looks at removing a second fraction with x_W,A,2 = 0.30.

  1. An alternative equivalent calculation is to use the entire cumulative area and the original feed F = 1 kmole. Show that this alternate calculation of W(at x_W,benzene = 0.30) gives the same result.

  2. When x_W,benzene = 0.30, what are the values of x_W,toluene and x_W,cumene?

  3. For the fraction collected from x_W,benzene = 0.40 to x_W,benzene = 0.30, determine the values of D_total, x_{D,benzene,avg}, x_{D,toluene,avg}, and x_D,cumene,avg.

  D28. Repeat Problem 9.D13 except use Figure 9-10 as long as the distillate is in the two-phase region and then convert to simple batch distillation by bypassing the liquid-liquid settler. Compare the amounts and concentrations of the three products to Problem 9.D13.

  D29. A 10.0 mol% ethanol 90.0 mol% water feed is batch distilled at 1.0 atm. The batch distillation system consists of a still pot plus a column with the equivalent of nine equilibrium contacts and a total condenser. External reflux ratio = 2/3. The initial charge to the still pot is 1000.0 kg. The final still pot concentration is 0.004 mole fraction ethanol. Find W_final, D_total, and x_D,avg. Note: Stepping off ten stages for a number of operating lines sounds like a lot of work. However, after you try it once, you will notice that there is a shortcut to determining a relationship between x_D and x_W.

• E. More Complex Problems

  E1. We are doing a single-stage, batch steam distillation of 1-octanol. The unit operates at 760 mm Hg. The batch steam distillation is operated with liquid water present. The distillate vapor is condensed, and two immiscible liquid layers form. The feed is 90.0 mol% octanol, and the rest is nonvolatile organic compounds. The feed is 1.0 kmol. We desire to recover 95% of the octanol. Vapor pressure data for water are given in Problem 8.D15. For small ranges in temperature, these data can be fit to an Antoine equation form with C = 273.16. The vapor pressure equation for 1-octanol is in Problem 8.D11.

  1. Find the operating temperature of the still at the beginning and end of the batch.

  2. Find the amount of organics left in the still pot at the end of the batch.

  3. Find the kmoles of octanol recovered in the distillate.

  4. Find the kmoles of water condensed in the distillate product. To do this, use the average still temperature to estimate the average octanol vapor pressure, which can be assumed to be constant. To numerically integrate Eq. (9-23b) relate x_org to n_org with a mass balance around the batch still.

  5. Compare with your answer to Problem 8.D11. Which system produces more water in the distillate? Why?

  E2. We wish to use batch steam distillation at 1.0 atm to recover 1-octanol from 100.0 kg of a mixture that is 15.0 wt% 1-octanol, and the remainder consists of nonvolatile organics and solids of unknown composition. The still pot is operated with liquid water in the pot. Assume the still pot is well mixed and liquid and vapor are in equilibrium. Ninety-five percent of the 1-octanol should be recovered in the distillate. Assume that water is completely immiscible with 1-octanol and with the nonvolatile organics. Because the composition of the nonvolatile organics is not known, we do a simple experiment and boil the feed mixture under a vacuum with no water present. The result is that at 0.05 atm pressure, the mixture boils at 129.8°C.

  1. Find the mole fraction of 1-octanol in the feed and the effective average molecular weight of the nonvolatile organics and the solids. (Note: This is identical to the solution of part a in Problem 8.D15.)

  2. Find the kg and kmole of 1-octanol in the distillate, the kg of total organics in the waste, and the 1-octanol weight fraction and the 1-octanol mole fraction in the waste.

  3. Find the initial and final values of the temperature and of VP_octanol in the still pot. A spreadsheet or MATLAB is highly recommended for finding T and VP.

  4. Find the kg and kmole of water in the distillate. This requires a numerical integration of Eq. (9-23b); however, the problem is simplified in this case. Because the still-pot temperature does not change much, the value of (VP)_octanol is very close to constant, and the average value can be used.

  5. Compare the solution with the solution of Problem 8.D15. Why does batch steam distillation require less steam than continuous steam distillation?

  Octanol boils at about 195°C. The formula for octanol is CH₃(CH₂)₆CH₂OH, and its molecular weight is 130.23. Vapor pressure formulas for octanol and water are available in Problems 8.D11 and 8.D15, respectively.

  E3. In inverted batch distillation the charge of feed is placed in the accumulator at the top of the column (Figure 9-9). Liquid is fed to the top of the column. At the bottom of the column bottoms are continuously withdrawn, and part of the stream is sent to a total reboiler, vaporized, and sent back up the column. During the course of the batch distillation, the less volatile component (LVC) is slowly removed from the liquid in the accumulator, and the mole fraction MVC x_d increases. Assuming that holdup in the total reboiler, the total condenser, and the trays is small compared to the holdup in the accumulator, the Rayleigh equation for inverted batch distillation is

  ln (D_final /F) = – _xfeed∫^xd,final [(dx_d)/(x_d – x_B)]

  We feed the inverted batch system shown in Figure 9-9 with F = 10.0 mole of a feed that is 50.0 mol% ethanol and 50.0 mol% water. We desire a final distillate mole fraction of 0.63. There are two equilibrium stages in the column. The total reboiler, the total condenser, and the accumulator are not equilibrium contacts. VLE data are in Table 2-1. Find D_final, B_total, and x_B,avg if the boilup ratio is 1.0.

  E4. A nonvolatile solute is dissolved in 1.0 kmol of methanol. We wish to switch the solvent to water. Because the solution is already concentrated, a first batch distillation to concentrate the solution is not required. We desire to have the solute in 1.0 kmol of solution that is 99.0 mol% water and 1.0 mol% methanol. This can be done either with a constant-mole batch distillation or by diluting the mixture with water and then doing a simple batch distillation. VLE data (ignore the effect of the solute) are in Table 2-7. Dilute the original pure methanol (plus solute) with water and then do a simple batch distillation with the goal of having W_final = 1.0 and x_M,final = 0.01. Find the moles of water added and the moles of water evaporated during the batch distillation. Compare with the constant-mole batch distillation in Problem 9.D17.

  E5. A simple batch distillation is used to process 1.0 kmole of methanol-water feed into three distillate fractions and a waste. The initial feed has x_F,methanol = 0.50 mole fraction. We want the average mole fractions of methanol in the distillate fractions to be x_dist,avg,1 = 0.70, x_dist,avg,2 = 0.60, and x_dist,avg,3 = 0.40. Equilibrium data is in Table 2-7.

  Part a. Find W_1,final, D_total,1, x_W,final,1; W_2,final, D_total,2, x_Wfinal,2; and W_3,final, D_total,3, x_W,final,3.

  To make this problem tractable, the following procedure is suggested: Calculate relative volatility values 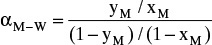from equilibrium data at x_M = 0.5, 0.4, 0.3, 0.2, 0.15, and 0.10. Over the different ranges of still pot mole fractions expected, calculate geometric average 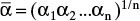for each range.

  Solve Eq. (9-13) on a spreadsheet to calculate W_fin using the guessed value of x_W,final. Calculate x_D,avg for the fraction. Use Goal Seek to make diff = x_{D,avg,specificed} – x_D,avg,guess approach zero by changing the guess for x_W,final. If the average value of relative volatility used was for an obviously incorrect range, insert a corrected 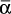, and repeat. Do this for each fraction.

  Part b. In the lab or plant, it is easier to collect fractions based on weight or time than based on mole fraction measurements. If heating is done at a rate of 20 kW, at what time in minutes should we switch from collecting the first fraction to collecting the second fraction? Required data are available in the textbook (see Appendix D in the back of book).

  E6. We are separating 100 moles of a feed that is 60.0 mol% methanol and 40.0 mol% water by batch distillation in a system with a still pot and a column that has one equilibrium contact (two equilibrium contacts total). Start the operation with a constant reflux ratio of L/D = 2/3. Operate with L/D = 2/3 until x_dist = 0.70. Then keep the distillate mole fraction constant by varying L/D. When L/D = 4.0, stop the batch distillation.

  1. Find x_W,final.

  2. Find W_final and D_total.

  3. Find x_D,avg.

• H. Computer Spreadsheet Problems

  H1. A mixture of benzene (A) and cumene (C) is to be distilled in a simple batch system. The initial charge of 5.0 kmol is 37.0 mol% benzene and 63.0 mol% cumene. At the system pressure of 1 atm and choosing cumene (C) as the reference component, the relative volatility is α_A–C = 10.71. Use Eq. (9-13).

  1. If FR_benzene,dist = 0.75, find x_A,Wfinal, W_final, D_total, and x_A,D,avg.

  2. If x_A,Wfinal = 0.05, find FR_benzene,dist, W_final, D_total, and x_A,D,avg.

  3. If FR_benzene,dist = 0.982, find x_A,Wfinal, W_final, D_total, and x_A,D,avg.

  H2. Run a simple batch distillation of a mixture of benzene (A), xylene (B), and cumene (C). Initial charge is 5.0 kmole that is 72.0 mol% benzene, 13.0 mol% xylene, and 15.0 mol% cumene. If x_A,Wfinal = 0.30, find W_final, x_W,B, x_W,C, D_total, x_D,A,avg, x_D,B,avg, and x_D,C,avg. Constant relative volatilities are benzene = 2.25, toluene = 1.0, xylene = 0.33, and cumene = 0.21. Note: Toluene can be the reference component despite not being part of the mixture.

  H3. Run a simple batch distillation of a mixture of benzene (A), xylene (B), and cumene (C). Initial charge is 2.7 kmole that is 64.3 mol% benzene, 11.6 mol% xylene, and 24.1 mol% cumene. If x_A,D,avg = 0.800, find W_final, x_W,A, x_W,B, x_W,C, D_total, x_D,B,avg, and x_D,C,avg. Constant relative volatilities are benzene = 2.25, toluene = 1.0, xylene = 0.33, and cumene = 0.21. Note: Toluene can be the reference component despite not being part of the mixture.